爆轰波斜冲击金属介质理论在聚能装药药型罩设计中的应用研究

张洋溢 ，龙 源，何洋扬 ，纪 冲，谢全民

(1.解放军理工大学 工程兵工程学院，南京 210007;2.北京理工大学 爆炸科学与技术国家重点实验室，北京 10081;3.北京63956部队，北京 100093)

爆轰波斜冲击金属介质理论在聚能装药药型罩设计中的应用研究

张洋溢12，龙 源12，何洋扬3，纪 冲12，谢全民1

(1.解放军理工大学 工程兵工程学院，南京 210007;2.北京理工大学 爆炸科学与技术国家重点实验室，北京 10081;3.北京63956部队，北京 100093)

将爆轰波斜冲击金属介质理论引入聚能药型罩罩高参数设计中，运用LS－DYNA显式动力学软件对爆轰波斜入射铜介质进行了仿真计算，得到了接触位置压力峰值P与入射角φ0之间的关系，数值仿真结果和理论计算值、试验值均吻合得较好。基于仿真计算和理论分析，得出了圆锥形和球缺形药型罩点起爆条件下罩高参数确定的工程算法，并将其应用于一种组合式战斗部的设计中。该方法为药型罩高度的确定提供了基于理论分析方面的设计依据，丰富了聚能装药战斗部的设计方法。

爆轰波;斜冲击;数值仿真;药型罩

TJ413

A

高能炸药平面爆轰波与金属平板的斜相互作用，近年来引起了国外许多著名学者的关注，Walsh［1］、Cheret［2］等人分别研究了炸药与 U、Cu及 Al平板的斜相互作用。而在聚能装药设计中，爆轰波与金属药型罩的相互作用，其作用过程本质上也是一个爆轰波斜冲击过程。

一直以来，对药型罩高度这一聚能装药重要参数的设计主要还是凭借经验、试验与数值模拟等手段来确定。用于分析聚能射流成型的经典理论——PER理论是基于圆锥形药型罩的假设，认为锥顶角和罩壁厚不变，起始爆轰波为平面波。但实际上，大部分聚能装药还是采用简单、可靠的单点起爆方式，起爆后在装药中传播的为一球面爆轰波，而非平面爆轰波。就目前的技术手段还很难生成绝对理论上的平面爆轰波，通常形成的是具有较大曲率半径的准平面波;且随着金属药型罩的形状越来越多样化(如：圆锥罩、球缺罩、喇叭罩、楔形罩和组合罩等)、更加细致的分析一般情况下的聚能装药成型过程，爆轰波入射角φ0的改变与变化就不能被忽略了。

基于上述原因，本文将炸药——金属接触爆炸领域的经典理论与算法引入到聚能药型罩罩高参数设计中，结合理论分析运用数值分析软件，对爆轰波斜入射铜介质进行了仿真计算，并将计算结果与前人的实验进行了比对，证明计算结果正确、有效，并得出了两种药型罩点起爆条件下，罩高参数确定的工程算法。

该研究为药型罩高度的确定提供了基于理论分析方面的设计依据，丰富了聚能装药战斗部的设计方法，能够对战斗部药型罩的设计提供技术支持。

1 爆轰波斜冲击金属介质作用理论计算

当爆轰波波阵面与介质表面呈一定角度向介质传播时，将发生爆轰波对介质的斜冲击现象。倾斜爆轰波传播到与炸药相接触的介质表面，向介质中传入一个斜冲击波，同时也向爆轰产物反射回来一个斜反射波，斜反射波可能是冲击波，也可能是膨胀波，其性质不仅与炸药、介质的物理特性有关，并且还与斜爆轰波的入射角度有关。另外，即使在爆轰产物内反射回斜冲击波，还有正规斜反射和非正规斜反射之分，其情况比爆轰波对介质垂直入射以及爆轰波对刚性壁面的斜反射问题都要复杂的多。以正规斜反射为例(如图1所示)，下面讨论一下爆轰波斜入射金属介质时各区流场参数计算方法［3］。

图1 正规斜反射现象Fig.1 Regular oblique reflection

图中OI为斜爆轰波入射波波正面，OI与相接触介质界面夹角为φ0;OR为返回爆轰产物中的斜反射冲击波的波阵面，OR与介质初始界面的夹角为φ2;OT为传入介质中的斜透射冲击波波阵面，OT与介质初始界面的夹角为φ3;介质在爆轰产物作用下发生变形，介质移动后的界面与介质初始界面之间的夹角为δ。这样，斜爆轰波、斜反射冲击波、斜透射冲击波和界面把整个图形分成五个区域：(0)区为未爆炸药，(1)区为斜爆轰波后爆轰产物区，(2)区为反射冲击波后爆轰产物区，(m)区为斜透射冲击波后介质受到扰动的区域，(m0)区为初始介质。

方程(1)、(2)式中ρ0为炸药密度，ρm0为m0区的密度，D为爆速，k为绝热指数，M1为与炸药流的速度有关的参量，a，b，为与材料性质有关的常数，只含有 φ2、φ3两个未知数，可以联立求解。由于方程比较复杂，具体计算时需要采用试探解法。

由上述可知，对于爆轰波斜作用于金属介质的问题，传统的理论计算求解法工作量庞大，不利于在工程实践中的推广与应用，故拟采用数值仿真方法进行对比分析研究。

2 爆轰波斜冲击金属介质数值仿真计算

2.1 模型的建立

由于本文研究的问题具有轴对称特点，因此为提高分析效率可以采用LS－DYNA软件进行二维数值模拟计算。计算模型使用solid 162二维实体单元，使用拉格朗日算法。计算中炸药为B炸药，金属材料为铜，数值模拟中采用的材料模型及相关参数分别见表1和表2。

表1 B炸药材料模型及JWL状态方程主要参数Tab.1 Material model and Equation of state of B explosive

为了得到各个不同φ0时金属材料中的相关冲击响应参数，设计了分析研究模型(见图2)。在该模型中，通过一次计算，可得到φ0从0°～90°变化范围内的金属材料动态响应结果。当爆轰波扫过φ0=90°处，根据文献［4］介绍此后爆轰波将进入拐角爆轰阶段，属非定常爆轰情况，故此处不作过多讨论。

表2 铜药型罩Steinberg材料模型主要参数Tab.2 Steinberg model of copper liner

计算模型中，头部高度［5］为一重要参数，根据Craig 和 Mader［6］的 实 验结果：对于B炸药，当爆轰波传播10 cm后即完成爆压增长过程，形成具有稳定C－J压力的爆轰波，因此确定其头部高度为10 cm;装药口径取6 cm(大于B炸药临界尺寸);金属铜材料为半径为3 cm的实体半圆。

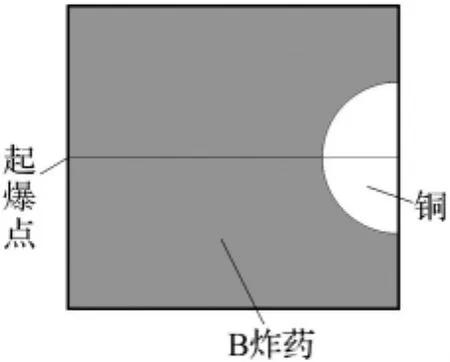
图2 计算分析模型Fig.2 Caculation analysis mode

2.2 计算结果与分析

将分界面处铜材料上各个单元压力峰值读出，经过反推得到不同单元处φ0值，最终得到图3中数值计算曲线，该图给出了随φ0的变化，铜材料表面所受到的斜冲击压力变化规律。当入射角为0°时正冲击压力为46.5 GPa;当 φ0=81°时，压力降低到32.1 GPa;在 φ0＞82.5°以后，分界面处发生了普朗特－迈耶尔膨胀，压力从C－J压力pH=28 GPa降低至21.8 GPa。

将模拟结果与文献［7］中给出的B炸药对铜板斜冲击压阻试验中得到的结果进行比较分析，见图3。从图3可以看出，数值模拟结果与试验压阻试验结果比较吻合，模拟值较试验值高约7.3%，小于10%，说明数值模拟是成功的。

但是在数值模拟、压阻试验中均未出现理论计算得到的由马赫反射引起的压力突越现象。Los Alamos实验室的学者们和法国学者 Cheret，Aveille等［8］采用测量受作用金属板自由表面速度的方法，研究了高猛炸药对铀合金的斜作用发现，按理想爆轰理论应在炸药中形成马赫杆的入射角下，金属中形成的冲击波压力的试验值竟比理论预告值低达35%，也未出现压力升高现象。

从前人的工作中可以得出，通过光学方法是可以观察到马赫杆的存在的;但是，用于计算马赫杆处流场压力的经典理论公式过于理想化，该计算方法是基于理想爆轰假设前提的，未能充分考虑到爆轰波阵面、马赫反射区等处的复杂流场环境，导致运用该方法不能对马赫反射区内流场参数进行有效计算。即使马赫反射区存在高于正冲击压力的高压区，其范围也是极小的，在工程应用特别是弹药工程方面的应用中，其贡献是不大的，可忽略。

图3 爆轰波对铜斜冲击时的p－φ0关系计算结果对比图Fig.3 Comarision of detonation wave

3 爆轰波入射角φ0对药型罩成形的影响

当聚能装药被引爆后，爆轰波波阵面与金属药型罩内表面之间势必存在夹角，定义波阵面切向与药型罩内表面切向夹角为入射角φ0。由前面的计算可知，随着φ0取值的变化，金属药型罩内表面微元所受到的爆轰波斜冲击作用强度是不同的。当φ0=0时，pm(药型罩内表面微元处压力)有最大值;当φ0逐渐增大后，pm逐渐减小。

就装药中心点起爆(最常见、可靠起爆形式)类型而言，当金属药型罩几何形状不同时，pm的变化规律也随之改变。下面以两种最为典型与常见的药型罩几何形状展开分析，得到它们各自相应的变化规律。

3.1 φ0的变化对圆锥罩的影响分析

当主装药为点起爆形式、药型罩呈圆锥状，球面爆轰波传递到药型罩内表面上任意位置处的斜入射情况如图4所示。

图中：O为起爆点;O'为锥罩顶点;L为装药头部高度［5］(已知量);α为圆锥罩半锥角(已知量)。当装药被引爆t时刻后，球面爆轰波传播之A处，此时其与药型罩之间的斜入射角为φ0，爆轰波传播方向与轴线方向夹角为β，O'A与AA'之间的夹角为γ。

图4 爆轰波斜作用于圆锥罩情况Fig.4 Oblique impact of detonation wave to cone liner

通过运用几何知识分析该图，得到φ0=γ+β关系。引入三角函数，最终得到：

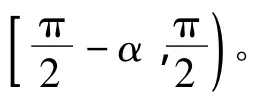
由图3可看出，当φ0大于某一临界值时由于发生膨胀反射，pm的值要低于C－J压力，这对于聚能装药技术来说是不利的。因此将发生膨胀反射的临界入射角度代入到式(3)中，就可以得到基于爆轰波斜反射理论的最大圆锥药型罩高度：

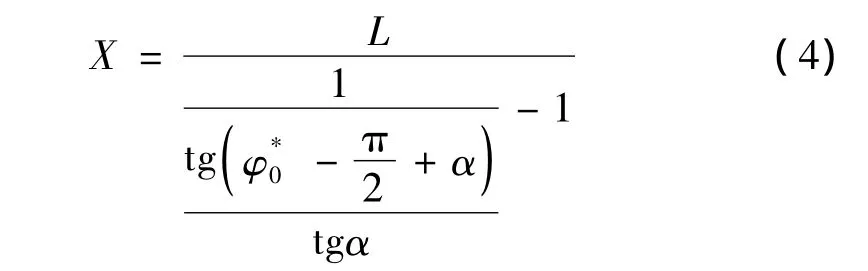
式中：X为基于斜反射理论的极限药型罩高度;φ*0为发生膨胀反射时的临界入射角;L为装药头部高度。此公式适用于点起爆条件下圆锥形(楔形)药型罩罩高参数设计。

对于给定锥角度数、装药头部高度的圆锥罩聚能装药，若药型罩过高则无疑会增加战斗部尺寸，且罩口部药型罩利用率低;若药型罩高度不足则战斗部威力达不到设计要求，未能完全有效利用炸药爆炸能量。而根据式(4)则可以确定最佳罩高。

3.2 φ0的变化对球缺罩的影响分析

当主装药为点起爆形式、药型罩呈球缺状，球面爆轰波传递到药型罩内表面上任意位置处的斜入射情况如图5所示。

图5 爆轰波斜作用于球缺罩情况Fig.5 Oblique impact of detonation wave to hemispherical liner

图中：O为起爆点;O'为球缺罩曲率中心;L为装药头部高度(已知量);α为球缺罩任意位置处所对应的圆心角(已知量)。当装药被引爆t时刻后，球面爆轰波传播之A处，此时其与药型罩之间的斜入射角为φ0，爆轰波传播方向与轴线方向夹角为β，O'A与AO之间的夹角为γ。

同样，通过运用几何知识分析该图，得到φ0=α+β关系。引入三角函数，最终得到

上式中x的物理意义为药型罩高度，通过将不同高度值代入式(5)可得到不同x处φ0的值，代入图3可知该位置的斜反射类型、反射区压力等参数，便于设计战斗部尺寸与外形时的相关参数的确定，提高设计效率与装药利用率。

式(5)中x为未知量式，其他均为可以通过上面的计算得到的已知量，因此解此一元二次方程同样可以得到基于爆轰波斜反射理论的最大球缺药型罩高度。

由上可知，为提高聚能装药战斗部成型侵彻体威力，可增加药型罩的外扩程度，充分利用小φ0区的高压效应。当药型罩外行为非规则外形时，如喇叭罩、组合罩等，可将其分段处理。每个子段的外形无外乎锥形或球形，可分解后分析。

4 实例分析

将上述分析手段引入到目前经常研究的组合式药型罩装药实例上［9］，由于该问题属轴对称问题，所以可以将问题简化为二维情况分析。装药点起爆t时间后(见图6)，一个球状爆轰波在装药内部传播，其波阵面与药型罩内表面的夹角不断变化，该种装药条件下不同位置处爆轰波斜入射金属药型罩角度的变化规律可通过前面的计算方法计算得到，结果如图7所示。图中，虚线表示圆锥罩从罩顶部到罩口部压力变化规律，由于圆锥结构自身斜率值不变，故该处压力值呈缓慢降低之势。因其所受压力值不是很高，可知圆锥段药型罩对炸药爆炸能量利用率不高，主要形成了质量较小但具有较大速度的金属射流。

图6 爆轰波对组合式药型罩的斜入射Fig.6 Oblique impact of detonation wave to group liner

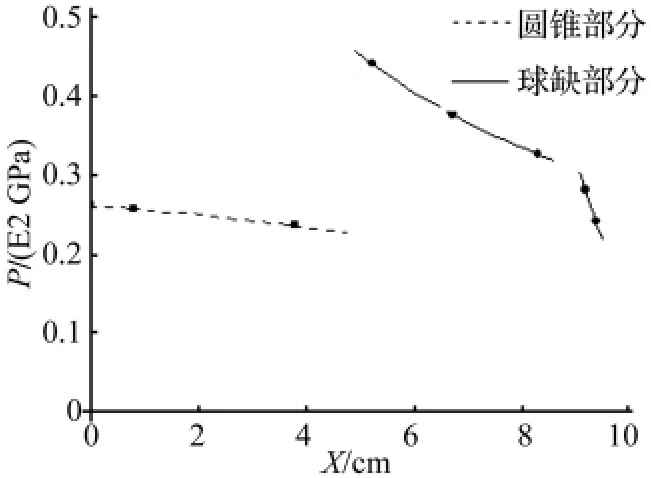
图7 组合罩不同位置处所受压力Fig.7 Pressure at different place of the group liner

实线则表示球缺段药型罩内表面不同位置处压力变化规律。从图中可以看出，实线段曲线明显高于虚线段曲线，说明此种装药结构下球缺罩获得了更多的爆炸能量，但随着球缺曲率的变化，入射角φ0大于了发生膨胀反射临界角度，此后压力骤降。金属微元运动速度降低，增大了成型侵彻体的速度梯度，使得最终形成杆式射流而非杆式弹丸。以上分析结果与文献［9］中得到的结果相吻合，说明本文得到的算法和分析方法是可行的，可以用来指导药型罩的设计。

5 结论

(1)对于爆轰波斜作用于金属介质的问题十分复杂，其中流场参数受到炸药种类、金属质地的共同影响，且随着入射角发生改变其反射波性质已发生较大变化，传统的理论计算求解法工作量庞大，很难又快又好地解决问题，不利于在工程实践中的推广与应用;

(2)通过引入现代成熟的爆炸力学分析软件对该问题进行系统模拟，并与理论分析相结合，本文采用的方法计算得到的结果与试验值和理论值均较为接近，满足工程应用精度，较传统理论计算方法快捷、准确，有工程推广价值。

(3)本文得到的两种药型罩点起爆条件下罩高参数确定的工程算法具有较强的可行性，该算法可推广到任意起爆方式、任意药型罩形状的战斗部设计工作中。

［1］ Walsh J M.On the problem of the oblique interaction of a detonation wave with an explosive－metal interface［A］.Shock Waves in Condensed Matter［C］.1987：3 －10.

［2］ Aveille J.Carion N，Vacellier J.Experimental and numerical study ofoblique interactions ofdetonation waves with explosive/solid material interfaces［A］.Ninth Symposium(International)on Detonation［C］.1989：842 －852.

［3］张守中.爆炸与冲击动力学［M］.北京：兵器工业出版社，1993，4.

［4］孙锦山，朱建士.理论爆轰物理［M］.北京：国防工业出版社，1995.

［5］王树魁，贝静芬，等译.成形装药原理及其应用［M］.北京：兵器工业出版社，1992，2.

［6］ Mader C L，Craig B G.LA －5865，1975.

［7］张宝平，姜春兰，洪 兵，等.爆轰波在金属板面斜反射现象的实验观测与分析［J］.北京理工大学学报，1992，12(1)：26－33.

［8］ Cheret R，Aveille J，Carion N.Emergence one detonation C－J.Sur le board libra un domain explosive［C］.R.Aced.Sc Paris，T.303.SeriesⅡ，No.I.1986.

［9］何洋扬，龙 源，等.圆锥、球缺组合式战斗部空气中成型技术数值模拟研究［J］.火工品，2008(4)：33－37.

Application of oblique impact theory of detonation waves at the explosive-metal interface in design of shaped charge

ZHANG Yang－yi1，2，LONG Yuan1，2，HE Yang－yang3，JI Chong1，2，XIE Quan－min1，2

(1.Engineering Institute of Engineer Corps，PLA University of Science and Technology，Nanjing 210007，China;2.State key Laboratory of Explosion Science and Technology，BIT，Beijing 10081，China;3.63956 Units，Beijing 100093，China)

The oblique impact theory of detonation waves at the explosive－metal was applied in design of shaped charge.Relationship between the pressure peak P on the interface of copper and incident angle φ0was obtained by using LS－DYNA.The numerical simulation results coincided well with the theoretical calculation ones and experimental data.An engineering method to calculate the proper liners height of tapered and spherical shaped lines was established under the condition of one－point detonation，it was applied in the design of a grouped liner warhead.The proposed method provided a basis to determine liner height，and enriched the design methods of shaped charge warhead.

detonation wave;oblique impact;numerical simulation;liner

北京理工大学爆炸科学与技术国家重点实验室开放式基金项目(KFJJ10－2M)

2010－04－26 修改稿收到日期：2010－06－28

张洋溢 男，博士生，1984年6月生