基于中心效应和临床界值的多中心临床试验评价方法学探讨

中国人民解放军第三○二医院(100039) 毕京峰 丁晋彪

基于中心效应和临床界值的多中心临床试验评价方法学探讨

中国人民解放军第三○二医院(100039) 毕京峰 丁晋彪△

△通讯作者：丁晋彪

多中心临床试验考虑中心效应进行疗效评价时，需参考临床界值(如等效界值或非劣效性界值)进行统计分析，但经对国内外文献检索，发现有关文献报道极少。有小部分等效性或非劣效性研究结果，基于中心效应检验无统计学差异的情况下，计量资料应用两组资料的t检验，分类资料应用两组资料的U检验，或应用均数或有效率的可信区间进行统计分析;多数文献未考虑中心效应，直接应用两组计量资料的t检验，或两组分类资料的U检验，或均数或有效率的可信区间进行统计分析。

由于各中心受试者的人种差异、年龄差异、病情差异等因素的影响，中心效应是客观存在的。在统计分析过程中所谓的中心间无统计学差异是基于概率论得出的，只能证明中心间差异无统计学意义，但无法避免中心效应客观存在的现实。而且，中心间差异无统计学意义的结论一般是基于α=0.05得出的，在这种结论基础上实现对疗效的统计分析，会增加犯Ⅰ类错误的概率。因此，建立基于中心效应和临床界值的疗效评价方法是当前临床试验中亟需解决的课题之一。

本研究对这一课题进行了长期的探索研究，并先后与四川大学循证医学中心、山东大学公共卫生学院、山东中医药大学卫生统计教研室的统计学专家和学者就相关关键技术问题进行了探讨，经过多次的建模后对该课题的研究取得了一定的突破，现将有关解决思路归纳如下。

多中心临床试验中计量资料基于中心效应和临床界值的疗效评价方法

〔1〕利用多重线性回归模型进行临床计量资料非劣效性评价的统计分析方法，应用该模型实现计量资料基于中心效应的临床疗效评价。

以治疗后数据为因变量，以各中心和试验分组为自变量，建立 μy=β0+β1group+β2x1+… +βmxm-1的多元线性回归方程。由于理论上不存在中心效应时，各中心两组总体均数之差均应为β1，因此，通过本回归方程即可得到两组整体均数差值的校正均数及其标准误，利用这两个关键数据即可以实现基于中心效应的疗效评价。

多中心临床试验中分类资料基于中心效应和临床界值的疗效评价方法

基于上述计量资料通过校正后均数差值和差值标准误实现了基于临床界值的疗效评价，分类资料能否实现对各中心有效率的校正则是分类资料基于临床界值进行疗效评价的关键环节。

目前尚未发现可以直接对有效率进行校正的统计方法，但CMH方法、Meta分析、logistic回归等几种统计分析方法实现了对OR值的校正。如果将临床界值换算成OR值，直接应用校正后的OR值进行比较检验，会出现差别较大危险。因此，不能直接应用OR值进行疗效评价。

本研究的解决思路是：能否应用校正后的OR值，实现对有效率的校正，并利用校正后的有效率实现基于临床界值的疗效评价。

1.目前应用临床界值实现分类资料疗效评价的主要方法

经对相关文献进行检索，目前国内外真正可以将临床界值纳入分类资料疗效评价的分析方法主要采取直接利用两组有效率的u检验或可信区间检验进行疗效评价，并未考虑中心效应。但该方法为我们提供了一个研究思路：如果能得到有效率的校正值，就可以利用这两个校正值的u检验或可信区间检验进行疗效评价。

2.CMH卡方检验可以实现对两组有效率优势比OR的校正

CMH卡方检验方法不仅可以在扣除中心效应的情况下提供卡方值，而且能够实现对两组有效率优势比OR的校正。OR值的公式为：OR=ad/bc，其中a、b、c、d分别是理想中校正后四格表的相关数据，共四个未知数。另外，我们还能得到两个方程：a+b=N1，c+d=N2。其中N1和N2代表两组的样本量，属已知数据。

由于按照四元方程的求解要求，需要4个方程式方可得出正确的结果，而目前只有三个方程式，因此，仅依据OR值无法实现对两组有效率的校正。

3.利用OR可信区间实现对每组有效率进行校正的思路

(1)建立方程及方程求解

仔细分析CMH给出的统计分析过程，其结果不仅仅提供了CMH检验的统计量和较正后OR值，还列出了OR值的可信区间。OR值可信区间的计算公式〔2〕为 OR1±1.96/X，其中X为 χ2值的平方根，而 χ2值则是对校正后两组OR值进行比较时的统计量。利用上述公式，代入OR值及可信区间的上限或下限，可以求得 χ2值。

由 χ2值的计算公式为〔3〕：χ2=(N1+N2-1)(ad-bc)2/［(a+b)(a+c)(c+d)(b+d)］，本研究找到了第四个方程式。

加上上面的三个方程式，构成了一个四元二次方程组，利用mathematic数学分析软件，可以得出两组校正后的a、b、c、d数据。

(2)两组答案的选择

由于所设方程组为四元二次方程，必然得出两组答案，必须对两组答案作出正确的选择。

经进一步研究发现，两组数据具有相同的组间差异，即分别计算试验组的有效率p1和对照组的有效率p2，两组资料p1-p2的值相同。分别计算合并标准误时，发现其合并标准误也相同。由于两组有效率比较时，u检验的公式为u=(p1-p2)/S¯X，可信区间的公式为(p1-p2)±Uα/2S¯X，因此，二组具有相同的u值和可信区间。另外，对校正后的四格表进行χ2检验时，两组具有相同的统计量。综合上述，本研究认为，两组资料可以选择任意一组，而不影响统计分析结果。

(3)基于临床界值的疗效评价

由于分类资料基于临床界值的疗效评价主要应用两组有效率的u检验或可信区间进行检验，皆基于p1-p2和S¯X进行计算，因此，可以顺利实现基于临床界值的疗效评价。

4.本方法的应用示范

通过某新药治疗原发性高血压的临床研究，得到数据见表1。

经用CMH检验，校正后的OR值为7.7189;可信区间为3.4071～17.4863。应用可信区间计算公式：OR1±1.96/X，利用上限或下限都可以得到χ2=23.9937。

第二组率的差值与标准误：p21=a2/62，p22=c2/60，p12-p22=0.43，Sp12-p22=0.078。χ2=24.1893。

从上述计算结果可以看出，两组率的差值、差值的标准误及χ2检验的统计量完全相同。

应用上述方法，实现了基于校正后OR值计算四格表的校正数据，从而可以利用校正后四格表的数据进行基于临床界值的疗效评价。

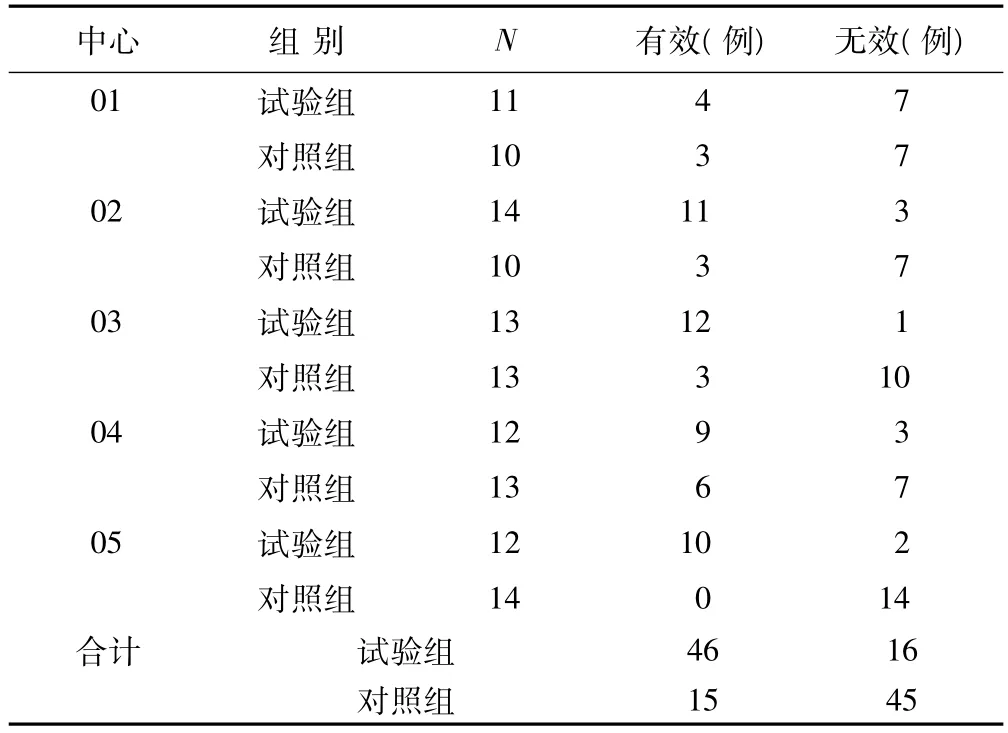
表1 某新药治疗原发性高血压的临床研究

由于logistic回归分析也可以实现对OR值的校正，本研究也利用logistic回归分析结果进行了计算。

logistic回归分析对OR值的校正结果是8.855，而用CMH方法的校正结果为7.7189，二者对OR的校正值不同。

依据logistic回归分析对OR值的校正结果，经计算，四格表的校正数值也略有差异，分别是：

其差值与标准误为：p1=a1/62，p2=c1/60，p11-p12=0.455，Sp11-p21=0.077。与应用 CMH方法计算的结果相比，只有微小差异，考虑这种差异可能与logistic回归是基于最大似然估计方法的误差有关。

综上所述，由于CMH可以对OR值进行校正，利用该校正后OR值及其可信区间能够实现对有效率的校正，从而可以解决分类资料基于临床界值考虑中心效应的疗效评价。鉴于目前国内外尚无对分类资料基于临床界值考虑中心效应进行临床评价的报道，如果对本研究成果深入研究，进一步证实其可靠性和科学性，将填补临床试验中该领域统计分析方法的空白。

参考文献

1.金欢，罗剑锋，李宝月.校正中心效应的非劣性检验.中国卫生统计，2007，12，24(6)：562-564.

2.颜虹.医学统计学.人民卫生出版社，北京：2005，7：96-98.