基于ARCH族模型的海西州地区呼吸道感染发病情况研究*

西北民族大学计算机科学与信息工程学院(730030) 马亮亮 田富鹏

基于ARCH族模型的海西州地区呼吸道感染发病情况研究*

西北民族大学计算机科学与信息工程学院(730030) 马亮亮△田富鹏

*：国家自然科学基金资助项目(60673192)

△通讯作者：马亮亮，E-mial：mll198684@126.com

呼吸道感染是危害人们健康的一种发病率较高的疾病，由于人们生活水平的提高、工作压力的增大和不良的饮食习惯及其他原因，近年来呼吸道感染发病率有增加的趋势。通过建立数学模型，研究呼吸道感染和平均气温之间的相互关系，可以帮助我们更好地认识和及时预防呼吸道感染，有效地降低呼吸道感染对人们的危害，从而保障人们的生活质量。

基础数据和统计学方法

1.病历资料来源

全部发病资料取自青海海西州第一人民医院。经过核对、补漏，从而保证资料的准确和完整。

2.统计学方法

运用Excel 2003及EViews 3.1对2001年1月至2007年12月的海西州地区呼吸道感染发病资料进行整理分析，统计出了海西州地区的呼吸道感染月发病率和月平均气温，通过建立ARCH、ARCH-M、GARCH、GARCH-M、TARCH、TARCH-M、EGARCH、EGARCHM、CARCH和CARCH-M模型，并对所建模型中的残差序列进行独立性检验、利用所建模型对海西州地区的呼吸道感染实际发病率进行拟合，从中选出最优模型，对呼吸道感染的发病情况进行研究。

ARCH族模型简介

1.ARCH效应检验

设序列xt和yt分别表示海西州地区2001年1月至2007年12月的呼吸道感染月平均气温和月发病率。以月平均气温为因变量，为了考察变量间的动态影响，故采用分布滞后模型(通过反复试验，选取了一个相对较好的模型形式)，其形式为：

其参数估计及相关检验结果如表1所示。

从表1可知，所有系数的统计学检验对于90%的置信度均通过，且该模型的拟合优度达0.9315，说明整体效果不错。所建分布滞后模型对应的数学表达式为：

表1 分布滞后模型估计与检验结果

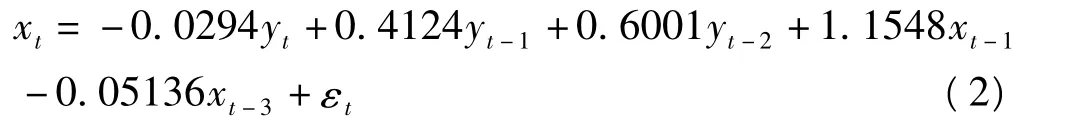
对模型(2)中的残差序列做ARCH效应检验。当χ2检验阶数即q值为8时，ARCH效应的检验结果显示，F=1.970356，相伴概率为0.024564，LM 统计量=14.42686，相伴概率为0.03130。

因此，在q=7时相伴概率p=0.0313，小于α=0.05水平，故序列存在高阶 ARCH效应，即存在ARCH-M、GARCH、GARCH-M、TARCH、TARCH-M、EGARCH、EGARCH-M、CARCH和CARCH-M 效应。

2.模型建立

基于模型(2)中的残差序列，分别建立ARCH、ARCH-M、GARCH、GARCH-M、TARCH 、TARCH-M、EGARCH、EGARCH-M、CARCH和 CARCH-M 模型。根据AIC和SC准则，并配合残差独立性检验比较发现，建立 ARCH(1)、ARCH(1，1)-M、GARCH(1，1)、GARCH(1，1)-M、TARCH(1，1)、TARCH(1，1)-M、EGARCH(1，1)、EGARCH(1，1)-M、CARCH(1，1)和CARCH(1，1)-M模型较为适宜。其条件方差的数学表达式分别为：

其中(7)和(8)式中dt是一个名义变量

上述模型中，模型(4)、(6)、(8)、(11)和(14)均是在回归模型中加入标准差后得到的结果。

3.模型检验

在上述所建的模型(3～15)中，模型ARCH(1)、ARCH(1，1)-M、GARCH(1，1)、GARCH(1，1)-M、TARCH(1，1)、EGARCH(1，1)、EGARCH(1，1)-M、CARCH(1，1)和 CARCH(1，1)所对应的参数 α1=0.1364 ＜ 1、α1=0.0576 ＜ 1、α1+ α2=-0.1115+1.0806=0.9691 ＜ 1、α1+ α2=0.0702+0.2834=0.3536＜1、α1+φ +θ1=2.2767-0.3262+0.0657=0.0162 ＜1、α1+ φ1+ θ1=0.2000+0.3839+0.2456=0.8295 ＜1、α1+ φ1+ θ1=0.2484+0.2026+0.0830=0.5340＜1、α+θ+ρ+σ=0.1044-0.0873+0.9707-0.1410=0.8468＜1、α+θ+ρ+σ=0.5717+0.1615-0.0919+0.6208=0.1187＜1均满足参数约束条件，即满足平稳条件。而模型TARCH(1，1)-M 中，参数α1+φ +θ1=-0.2349+0.4195+0.8597=1.0443＞1，不满足平稳条件，所以排除该模型。下分别对模型(3)、(4)、(5)、(6)、(7)、(10)、(11)、(12)和(14)中的残差序列进行独立性检验〔5〕，以确定所建模型的合理性。检验结果如表2所示。

表2 各模型残差独立性检验结果

由表2 可知，模型(3)、(4)、(5)、(6)、(7)、(10)、(11)、(12)和(14)的SIC和SC值均较小，可认为模型较好地拟合了原始数据。从整体角度考虑，模型ARCH(1，1)-M 的AIC和SC值(4.4190和4.6555)最小。因此，与其他模型相比较而言，模型ARCH(1，1)-M 的拟合度更高、最合理，即模型ARCH(1，1)-M 最优。

利用模型(3)～(14)(除13外)分别对海西州地区2001年1月至2007年12月的呼吸道感染月发病率进行拟合。

模型(3)～(14)(除13外)的残差序列拟合结果整体上均不错，但残差序列的拟合效果最好，因此基于原始数据建立的ARCH(1，1)-M模型是最优的。

结 论

由以上分析可知，由序列xt和xy(呼吸道感染月平均气温和月发病率)可建立分布滞后模型。通过对分布滞后模型中的残差序列进行ARCH效应检验，发现残差序列存在ARCH、ARCH-M、GARCH、GARCHM、TARCH 、TARCH-M、EGARCH、EGARCH-M、CARCH和CARCH-M效应。因此，基于分布滞后模型中的残差项可分别建立ARCH、ARCH-M 、GARCH和GARCH-M模型。最后，通过模型残差序列独立性检验和预测，选出了最优模型ARCH(1，1)-M。

本文中的数据是近7年的海西州地区呼吸道感染发病资料，海西州既是我国西北高原地区，又是我国少数民族聚集的地区，做好该地区呼吸道感染发病率的预测对高原少数民族地区人民的健康有重要的意义。尽管国家经济文化迅速发展，卫生条件得到改善，但是政府对这类疾病的预防不够重视，所以近几年来海西州地区呼吸道感染的发病率有逐年增高的趋势，这就提醒医疗卫生部门应加强对此高原少数民族地区呼吸道感染预防和控制的宣传工作。

1.刘晓冬，景睿，孟祥臻，等.ARIMA模型对中国人口死亡率预测的研究.中国卫生统计，2008，25(6)：630-631.

2.李存行，张敏，陈伟.自回归条件异方差模型在我国沪市的应用研究.数学的实践与认识，2008，38(8)：1-5.

3.张雪蓉，徐全智，杨晋浩.TARCH-M模型在上证指数波动率的实证分析.成都大学学报(自然科学版)，2006，3(25)：171-174.