二项分布若干性质的思考

●李 辉 (杭州外国语学校 浙江杭州 310023)

二项分布若干性质的思考

●李 辉 (杭州外国语学校 浙江杭州 310023)

我们知道:若离散型随机变量ζ的分布列为P(ζ =k)=Cknpk(1 －p)n－k，k=0，1，2，…，n，其中0≤p≤1，则称 ζ服从二项分布，记作 ζ～B(n，p)．二项分布的使用条件为:在n次独立重复试验中，某事件发生的次数即服从二项分布．二项分布是概率教学中一个非常重要的分布，本文通过对二项分布的一些思考，期望有助于读者对二项分布的理解．

例1在10件产品中有2件次品，连续抽3次，每次抽1件．

(1)当放回抽样时，求抽到的次品数ζ的分布列;

(2)当不放回抽样时，求抽到的次品数η的分布列．

解(1)根据题意容易求得ζ的分布列如表1所示．

表1 ζ的分布列

(2)根据题意可求得η的分布列如表2所示．

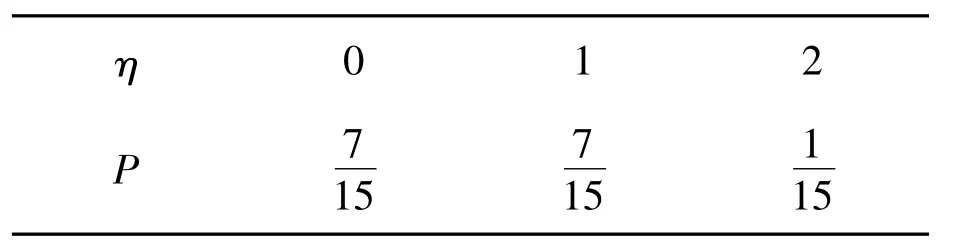
表2 η的分布列

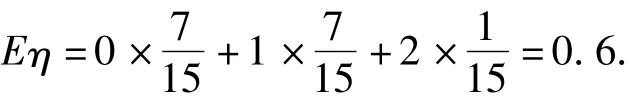
显然，2种不同的抽样方式并没有改变次品数的数学期望．

思考1放回与不放回为什么不影响数学期望?

问题一般化:设在N件产品中有M(M≤N)件不合格品，从中任取n(n≤N)件进行检查，求取得不合格品数ζ的数学期望．

这里，还假定取出的产品数不超过合格品总数，即n≤N－M．若没有这个假定，则随机变量ζ的取值范围应是 s，s+1，s+2，…，m，其中 m=min{M，n}，s=max{0，n－(N －M)}．在具体问题中不难理解，例如共有10件产品，其中次品数为6，从中取出5件产品，则取出的产品中次品数ζ的取值范围是 1，2，3，4，5．

(1)当放回抽样时，ζ服从二项分布

通过上述算式可以看出:放回与不放回确实不影响次品数的数学期望．我们也可以从另一个角度来理解:放回抽样是n次独立重复试验，每次取到次品的概率都是P=，概率本身就是一种“理想”，因此每次取到“理想”的次品数都是件，n次独立重复试验取到“理想”的次品数当然是np;不放回抽样等价于放回抽样．把每个产品看成由的次品和1－的合格品组成，可以认为每次取出一件产品，抽到次品的概率仍为，因此n次不放回的抽样等同于放回抽样，仍看作n次独立重复试验，即每次抽到次品的概率都是，故不放回的次品数的数学期望与放回的次品数的数学期望相等．这是一种对于放回与不放回不影响数学期望的朴素的理解方式．

思考2二项分布与其他分布有什么关系?

超几何分布与二项分布的关系:第一:在n次试验中，取得不合格品数X可能服从超几何分布或二项分布．当这n次试验是独立重复试验时，X服从二项分布;当这n次试验是不放回抽取时，X服从超几何分布．第二:在不放回n次抽取试验中，抽到的次品数X服从超几何分布．但是当产品的数目N很大时，因为

所以X的分布列近似于二项分布，并且随着X的增加，这种近似的精确度也会增加．

两点分布与二项分布的关系:若随机变量X的分布列具有表3所示的形式，则称X服从两点分布，p=P(X=1)称为成功概率．

表3 X的分布列

容易求得

两点分布是最简单的离散型随机变量，它是二项分布的基础，也是二项分布的一个特例，即n=1时的二项分布．二项分布可以看作是两点分布的一般形式，因为n次独立重复试验每次的数学期望都是p，所以从整体上看n个独立的两点分布即为二项分布，它的期望当然是n个期望的和，即

几何分布与二项分布的关系:若离散型随机变量ζ的分布列为

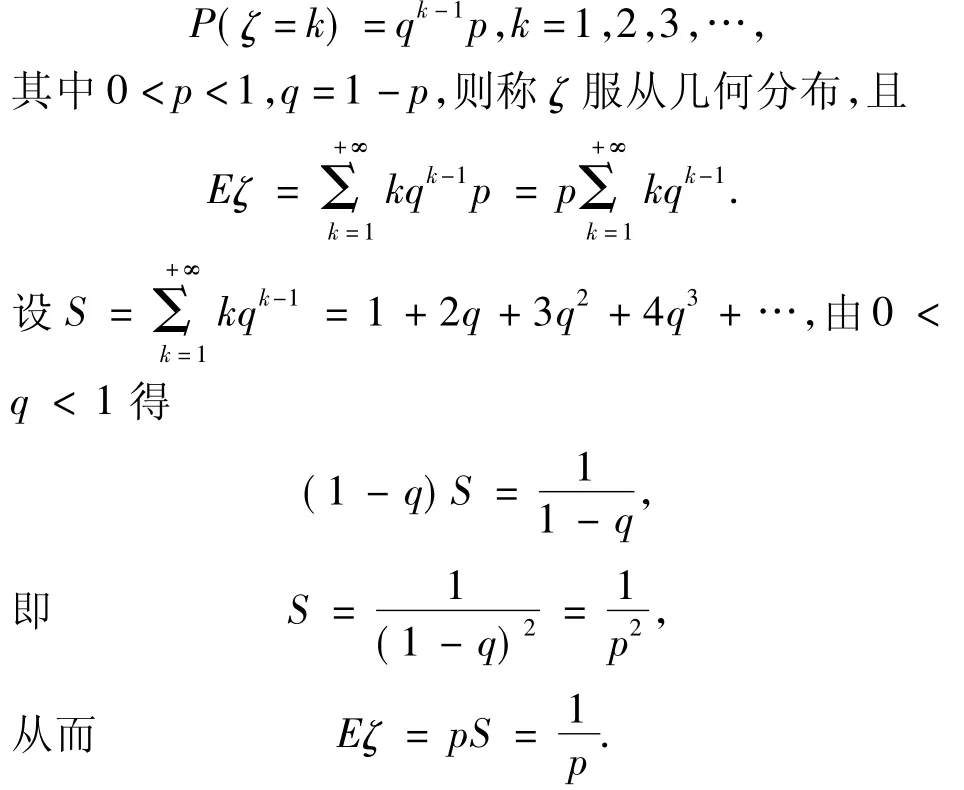
另外在二项分布中，n的值是确定的，ζ的取值是变化的，Eζ是由n和p决定的，但若反过来认为n的取值是可变的，n=1，2，3，…，则 ζ=1 始终成立，即Eζ=1．又因为几何分布也是独立重复试验，即每次试验事件发生的概率p也是不变的，所以

这时，几何分布和二项分布只是一个问题的2个方面罢了，关键是哪个量作为随机变量．

思考3如果二项分布的数学期望是np，那么服从二项分布的随机变量取何值时的概率是最大的?

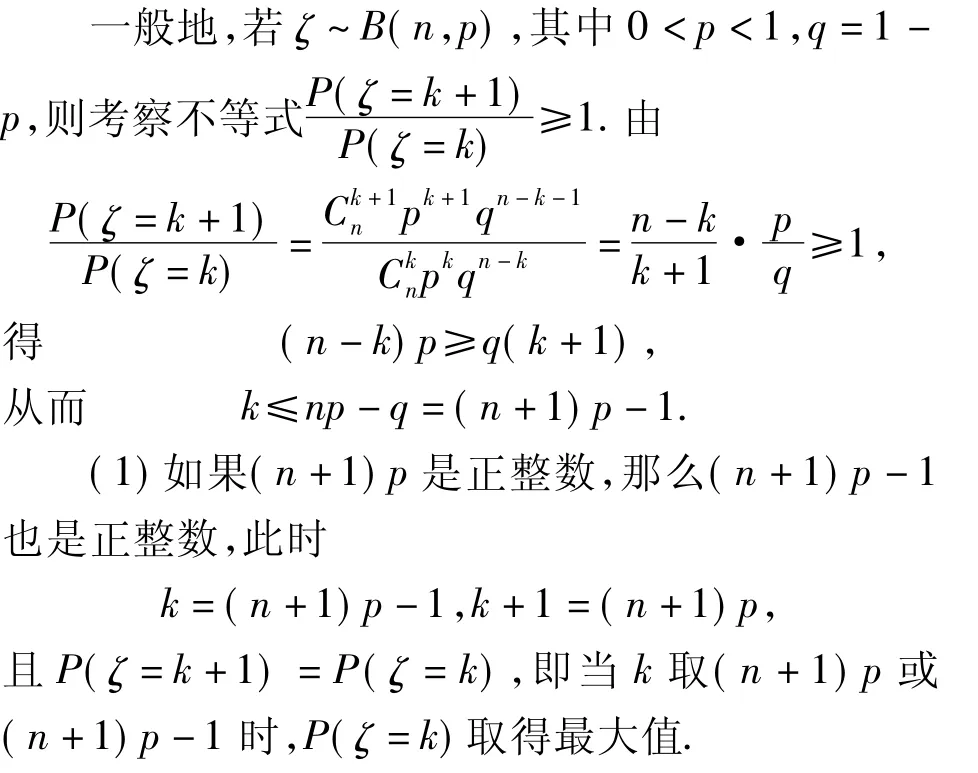
我们可以看出在二项分布的数学期望附近的概率达到最大值，这具有一种必然性．因为数学期望反映了随机变量取值的平均水平，通过大量的随机试验，有大量的随机变量的取值相对聚集在平均水平附近，所以随机变量在数学期望附近的概率达到最大值．

数学期望本身就是一种“数学理想”，概率也是一种“数学理想”．对于“理想”的理解更有助于我们对于概率概念的理解．概率是发生于大量的随机试验中的，只要这个试验的次数足够地多，频率就逐渐地趋向于概率．概率是一个理论值．只要这个试验的次数足够地多，试验出来的随机变量的平均值就会趋向于这个随机变量的理论的平均值，即它的数学期望．它是一个平衡点，具有一种必然性，是发生于大量偶然中的必然．