简述一道中考题的拓展与探究
2011-02-02陈明儒东海实验学校浙江宁波315800
●陈明儒 (东海实验学校 浙江宁波 315800)
简述一道中考题的拓展与探究
●陈明儒 (东海实验学校 浙江宁波 315800)
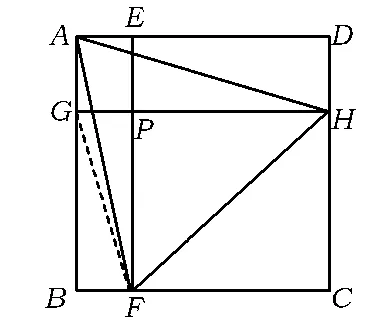
图1
题目如图1,边长为1的正方形ABCD被2条与边平行的线段分割成4个小矩形,EF与GH交于点P.
(1)若 AG=AE,证明:AF=AH;
(2)若∠FAH=45°,证明:AG+AE=FH;
(3)若Rt△GBF的周长为1,求矩形EPHD的面积.
(2009年广东省广州市数学中考试题)
1 试题评析
本题主要考查正方形、矩形、全等三角形等基础知识;考查计算能力、推理能力和空间观念;考查学生运用所学知识寻找问题关键点的能力.特别是在第(2)小题中,知道了∠FAH=45°后,利用∠HAD+∠BAF=45°打开解题思路是这个问题解决的关键所在,也是思维水平提升到更高层次的基本要素.试题不仅关注学生观察事物的能力和对数学知识层次理解的能力,也是对教学过程中学生推理演算能力的体现,具有较好的创新性.
2 试题拓展与探究
2.1 弱化条件,结论不变
对试题第(2)小题纵向拓展.
探究1若将条件放宽,如图2所示,在四边形ABCD中,AB=AD,∠B=∠D=90°,∠FAH=∠BAD,则结论BF+HD=FH是否仍然成立?

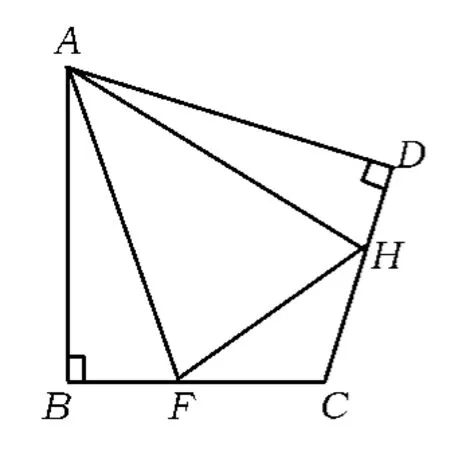
图2

图3
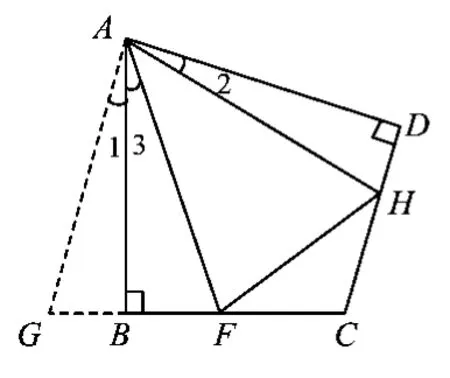
图4
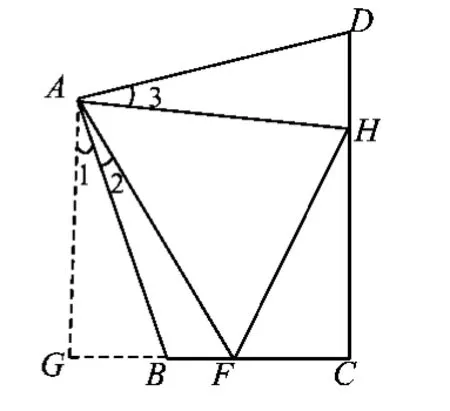
图5
在图5中,延长CB至点G,使得BG=DH,连结AG.由∠ABG和∠D都是∠ABC的补角,得
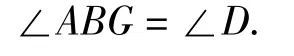
类似地,可以证明FH=BF+HD成立.
若将图1、图2、图3中的△FAH绕顶点A旋转至四边形外,则还可以继续探究FH,BF,HD之间的数量关系.
2.2 题设不变,探究结论
探究2对试题第(2)小题,当∠FAH=45°时,除本题的结论外,还可得到其他许多结论,可参见文献[1].除此之外,通过探究还发现:
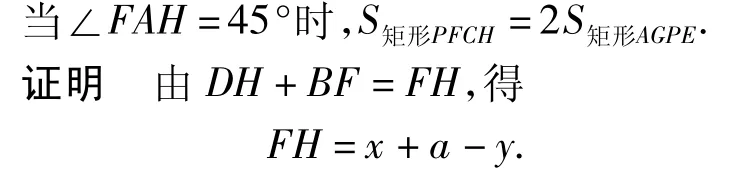
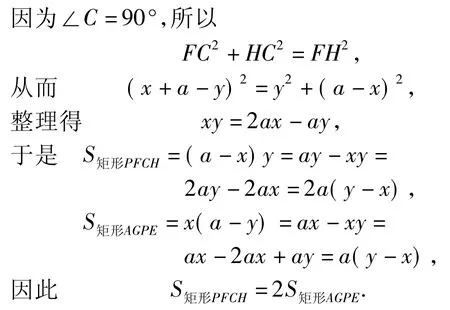
2.3 逆向思维,横向拓展


图6
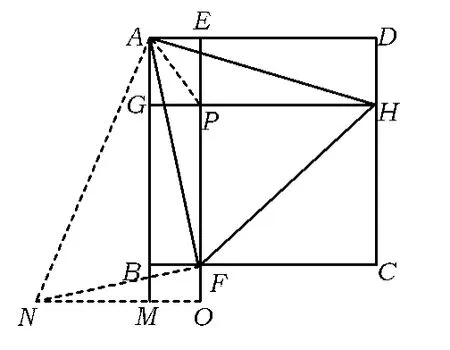
图7
方法2(运用旋转变换)如图7,将Rt△ADH绕点A沿顺时针方向旋转90°至Rt△AMN,延长线段NM与直线 EF交于点Q,连结 NF.设正方形AGPE 的边长为 a,PH=x,PF=y,则
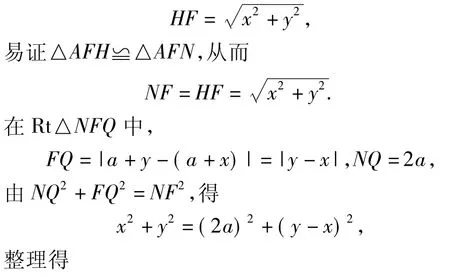
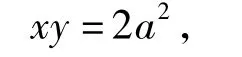
于是 S矩形PFCH=2S正方形AGPE.
方法3(运用基本图形)如图8,设正方形AGPE的边长为 a,EM=m,GN=n,PH=x,PF=y.由 ∠FAH=45°,即∠MAN=45°,得
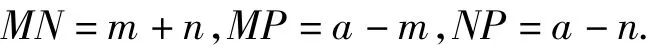
由△AEM∽△HPM得

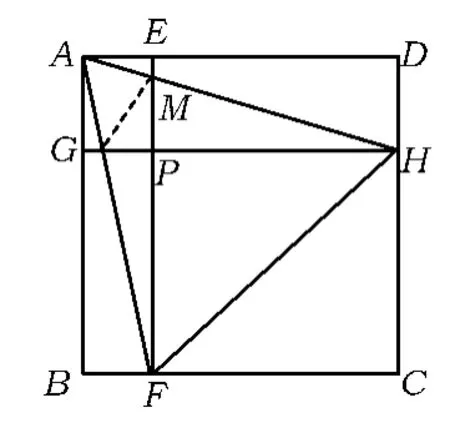
图8
2.4 从特殊到一般拓展
对试题第(3)小题,从特殊能否推到一般呢?
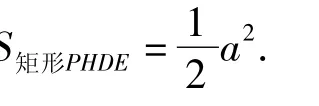
证明如图1,连结 GF.设 BF=x,则
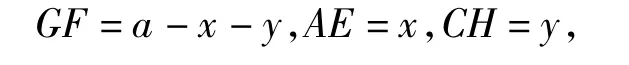
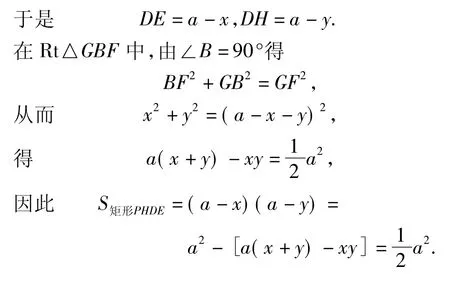
3 创编探究性问题
通过逆思2可以得到命题:在矩形ABCD中,若四边形 AGPE为正方形,且∠FAH=45°,则S矩形PFCH=2S正方形AGPE.
如果将这个命题作为普通的测试题,那么图形背景太复杂,起点也高.通过进一步思考,去掉一些不必要的线段,可以使图形更简洁.同时,增设2个有层次的问题,再植入旋转背景,把静态问题变为动态的探究性问题,这样符合现行的命题趋势.现创编如下:
正方形ABCD的边长为 a,点 E,F分别在边BC,DE的延长线上,∠EAF=45.
(1)若 CE=CF,如图9,证明:
①AE=AF;
②S△CEF=a2.
(2)让∠EAF绕点A旋转一定角度,使得CE≠CF,如图10,则△CEF的面积是否发生改变.若不改变,请给出证明;若改变,求改变后的△CEF的面积.
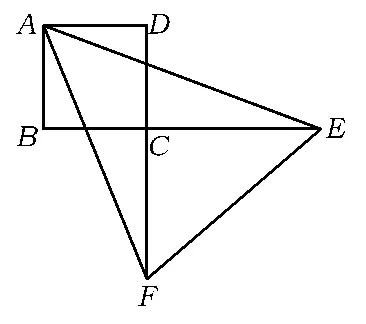
图9

图10
综上所述,适当对问题进行拓展与探究,使学生能充分感知到知识间的内在联系,加深对知识的纵横向认识,从而开阔了学生的视野,也培养了学生的探究和创新精神.
[1] 罗增儒.巧思妙解与数学证明[J].中等数学,2005(3):17.
