简述考查学生数学猜想的几种常见方式
2011-02-02李树臣沂南县教育局山东沂南276300
●李树臣 (沂南县教育局 山东沂南 276300)
简述考查学生数学猜想的几种常见方式
●李树臣 (沂南县教育局 山东沂南 276300)
《全日制义务教育数学课程标准》(以下简称《标准》)非常强调对学生猜想能力的培养.例如,在“基本理念”中指出:“学生的数学学习内容应当是现实的、有意义的、富有挑战性的,这些内容要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动”;在“设计思路”中指出,“推理能力主要表现在:能通过观察、实验、归纳、类比等获得数学猜想,并进一步寻求证据、给出证明或举出反例”;在阐述课程目标时指出,让学生“经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,能有条理地、清晰地阐述自己的观点”等等.由此可见,在数学教学中培养学生的数学猜想能力非常重要.可喜的是,最近几年的数学中考命题者在这方面进行了有益而大胆的探索,试卷中出现了一些引导学生去猜想的题目.为此,笔者从2010年各地的中考试卷中选择部分有代表性的题目进行分析,以供参考.
1 从算式的计算中,归纳猜想规律

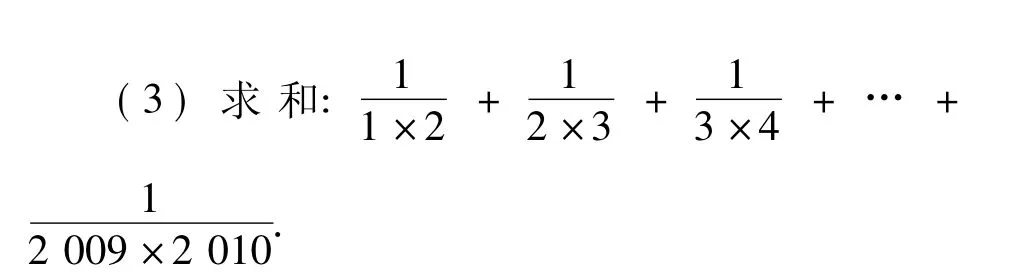
(2010年山东省济宁市数学中考试题)
分析本题以简单的分数计算为载体,以考查学生归纳猜想的能力为主.(1)观察给定的3个等式,即可猜想得到结论;(2)根据分式加减运算法则通分计算;(3)根据第(1)小题的结果计算.

点评给定几个代数计算式子,在计算的过程中通过归纳、猜想得到有关的规律,然后用代数变形的方式证明猜想的正确性,并利用猜想得到的规律解答给定的问题,这是一种常见的题型.解答这类问题需要有较强的观察、分析、判断、类比归纳等能力.在教学过程中,教师应结合具体的教学内容设计一些类似的题目让学生去分析和思考,学生的归纳猜想能力必将得到较大的提高.
2 与数形结合思想联系在一起,探索并猜想有关规律
案例2 用棋子按下列方式摆图形(如图1所示),依照此规律,第n个图形比第n-1个图形多__枚棋子.
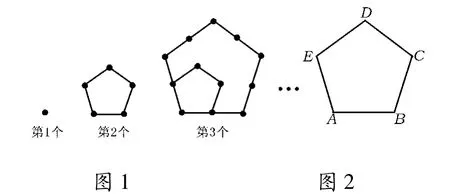
(2010年江苏省徐州市数学中考试题)
分析本题创设了一个观察棋子图形中棋子个数的“数形结合”的数学模型.在解答时,需要从简单到复杂进行探究:
第1个图形显然有1枚棋子;
第2个图形有5枚棋子,它们分别在一个正五边形的顶点处.为了便于分析,构造正五边形ABCDE,把五边形一个顶点A看成是第1个图形的一个点,这一点A是五边形的边AB和AE的交点.除这2条边外,还有3条边BC,CD,DE,每边上有2个点,这样还有3×2=6个点,但其中C,D这2个顶点计算了2次,应减去,这样就还有3×2-2=4个,即第2个图形有1+3×2-2=5枚棋子.
第3个图形比第2个图形多一层五边形,内层五边形就是第2个图形,有5枚棋子.外层五边形每边上3枚棋子,类比第2个图形,可计算第3个图形中棋子的枚数为:5+3×3-2=12个.
同样,第4个图形中棋子的枚数为
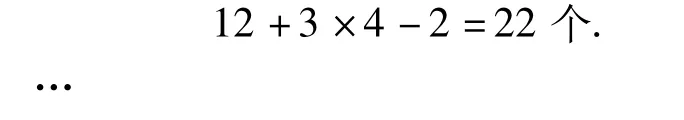
由此可以猜想得到规律:第n个图形中棋子的枚数是第n-1个图形中棋子的枚数加上3×n-2,这里3×n-2=3n-2就是增加数.
点评从分析的过程看,本题是借助于“图形”的形象性与直观性逐步得到解决的.除了考查学生的数学猜想能力外,还渗透了数形结合的思想.本题给我们的启发有二:一是在数学学习中,当遇到一个问题涉及到很多或无穷多情形时,可以从问题的简单情形或特殊情形入手,通过简单情形或特殊情形的试验,从中发现一般规律或作出某种猜想,从而找到解决问题的途径;二是在教学中,千万不要就知识点而讲知识点,一定要把这些“显知识”背后所“隐含”的数学思想揭示出来.做到用数学思想方法来“统领”知识点,以达到优化知识结构的目的,因为只有这样被“优化”起来的知识结构才具有生命力和创造性.
3 从对简单几何体模型的观察出发,猜想几何体中有关元素之间的数字规律
案例3十八世纪瑞士数学家欧拉证明了简单多面体顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型(如图3所示),解答下列问题:
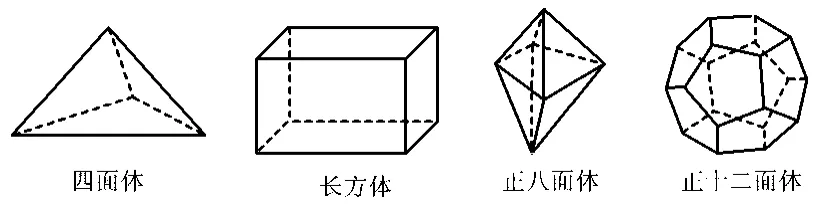
图3
(1)根据上面多面体模型完成表1中的空格,可得出顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,如表1所示.

表1 顶点数(V)、面数(F)、棱数(E)的数值表
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是__ .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是__ .
(3)某个玻璃饰品的外形是简单多面体,它的外表面由三角形和八边形这2种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.
(2010年浙江省宁波市数学中考试题)
分析(1)仔细观察给定的4个多面体模型,可知四面体的棱数为6,正八面体的顶点数为6;根据给定的4个多面体的顶点数(V)、面数(F)和棱数(E)之间的数量关系,可归纳、猜想得到它们之间的关系为V+F-E=2.(2)根据第(1)小题的结论求解.(3)多面体的面数为x+y,棱数为=36条.根据题意可列出一个方程,在求解时应把x+y当作一个整体.

点评 欧拉是一位著名数学家,他渊博的知识、无穷无尽的创作精力和空前丰富的著作令世人惊叹不已.本题的特点是给出几个几何体模型,让学生观察它们的顶点数、面数及棱数,为了启发学生能独立猜想到每个几何体模型的这“3个数量”之间的关系,即猜想得到著名的欧拉公式.本题用图表给出这些数中的大部分数,这样可降低解题难度.学生一旦猜想到它们之间的关系,后面的问题就可以直接利用这一关系进行解答.
4 通过创设具体的问题情境、数学实验等,考查学生数学猜想能力
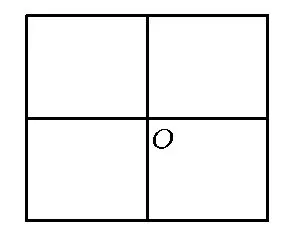
图4
案例4 问题再现在现实生活中,镶嵌图案在地面、墙面乃至服装面料设计中随处可见.在八年级课题学习“平面图形的镶嵌”内容时,对于单种多边形的镶嵌问题,主要研究了三角形、四边形、正六边形的镶嵌.在此把正多边形的镶嵌作为研究问题的切入点,提出其中几个问题来共同探究.
我们知道,可以单独用正三角形、正方形或正六边形镶嵌平面.如图4,若用正方形镶嵌平面,则可以发现在一个顶点O周围围绕着4个正方形的内角.
试想:若用正六边形来镶嵌平面,则在一个顶点周围应该围绕着__ 个正六边形的内角.
问题提出如果要同时用2种不同的正多边形镶嵌平面,那么能设计出几种不同的组合方案?
问题解决 猜想1是否可以同时用正方形、正八边形这2种正多边形组合进行平面镶嵌?
分析可以将此问题转化为数学问题来解决.从平面图形的镶嵌中可以发现,解决问题的关键在于分析能同时用于完整镶嵌平面的2种正多边形的内角特征.具体地说,就是在镶嵌平面时,一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角.
验证1在镶嵌平面时,设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意得

结论1在镶嵌平面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角,因此可同时用正方形和正八边形这2种正多边形组合进行平面镶嵌.
猜想2是否可以同时用正三角形和正六边形这2种正多边形组合进行平面镶嵌?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.
上面探究了同时用2种不同的正多边形组合镶嵌平面的部分情况,仅仅得到了一部分组合方案,相信同学们用同样的方法,一定会找到其他可能的组合方案.
问题拓广请你仿照上面的研究方式,探索出一个同时用3种不同的正多边形组合进行平面镶嵌的方案,并写出验证过程.
(2010年山东省青岛市数学中考试题)
分析本题从日常生活中的“镶嵌”问题出发,可分如下4个阶段展开:问题再现——问题提出——问题解决——问题拓广.
(1)在问题再现阶段,要求学生观察图4,回答用正六边形来镶嵌平面,在一个顶点周围应该围绕着几个正六边形的内角?这非常简单,学生都能类比猜想得到结论为3.
(2)提出问题:如果要同时用2种不同的正多边形镶嵌平面,那么能设计出几种不同的组合方案?
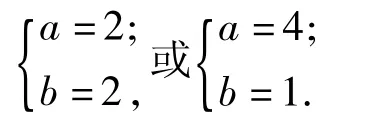
结论2在镶嵌平面时,在一个顶点周围围绕着2个正三角形和2个正六边形的内角或者围绕着4个正三角形和1个正六边形的内角可以拼成一个周角,因此可以同时用正三角形和正六边形这2种正多边形组合进行平面镶嵌.
猜想3是否可以同时用正三角形、正方形和正六边形这3种正多边形组合进行平面镶嵌?
验证3在镶嵌平面时,设围绕某一点有m个正三角形、n个正方形和c个正六边形的内角可以拼成一个周角.根据题意得
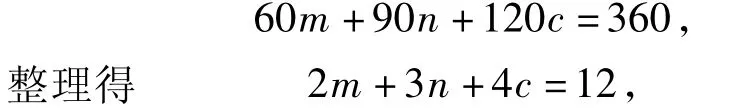
因此可找到惟一一组适合方程的正整数解为
(3)在问题解决阶段给出了2个猜想,为了降低难度,题目对猜想1进行了分析和验证并在得到结论1之后,提出了猜想2.对于这个猜想要求学生仿照对猜想1的验证过程,对猜想2进行验证,并归纳得出结论2.
(4)在问题拓广阶段,要求学生自己提出猜想、进行验证、最后归纳出结论.
本题的特点是引导学生进行“阅读—理解—猜想—验证”,文字叙述较长,如果学生不认真进行分析,那么可能会无从下手.解答的关键在于仔细“审题”,理解题意.
验证2在镶嵌平面时,设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角.根据题意得
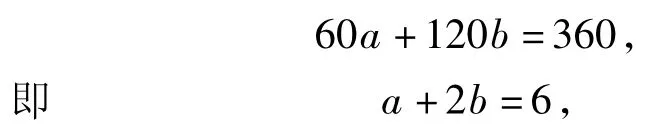
因此可找到2组适合方程的正整数解为
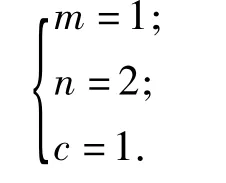
结论3在镶嵌平面时,在一个顶点周围围绕着1个正三角形、2个正方形和1个正六边形的内角可以拼成一个周角,因此可以同时用正三角形、正方形和正六边形这3种正多边形组合进行平面镶嵌(说明:本题答案不惟一,符合要求即可).
点评近年来,各地中考卷中经常出现这样的问题:提供一个学生熟悉的生活材料,要求学生能够从给出的问题情景中经过分析找到解决问题的规律和方法,灵活运用有关知识加以解决.本题以学生熟悉的生活实际问题(镶嵌)为背景,通过“再现生活中的实际问题——提出问题——问题解决——问题拓广”,考查学生把能否“镶嵌”的问题转化为能否“拼成”一个周角的问题的能力,进而考查学生利用方程的知识解答问题的能力.解决这类问题需要有较强的阅读理解能力和数学猜想能力,一般思路是:类比具体的范例猜想得到解题方法和规律,“模拟”此方法和规律解答类似相关问题.从深层看,本题以“镶嵌”为背景,考查学生类比猜想、推理、论证的能力.
案例5 (1)操作发现如图5,在矩形ABCD中,E是 AD的中点,将△ABE沿 BE折叠后得△GBE,且点G在矩形ABCD的内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(2)问题解决保持第(1)小题中的条件不变,若 DC=2DF,求的值.
(3)类比探求 保持第(1)小题中条件不变,若 DC=n·DF,求的值.
(2010年河南省数学中考试题)
分析(1)在实验操作时,只要能确定矩形ABCD的边AD的中点E,按要求进行操作,将会发现GF=DF.仔细观察发现,连结EF,得Rt△EGF≌Rt△EDF.只要能猜想到这一点,问题就容易解决了.(2)要求的值,只要求出即可.因为BF=BG+GF=AB+GF=DC+DF,而 DC=2DF,所以考虑到△BCF是直角三角形,利用勾股定理BC2+FC2=BF2,得BC与DC的关系,进而得解.(3)类比第(2)小题即可求解.
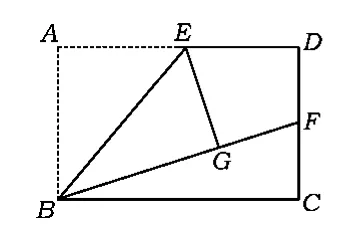
图5
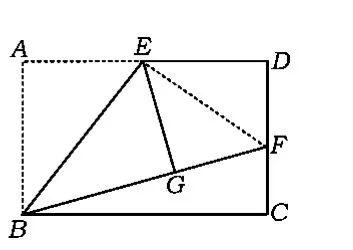
图6
解(1)同意.如图6,连结EF,则
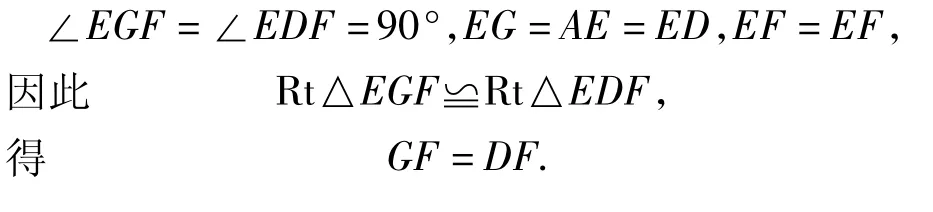

点评在最近几年的中考试卷中,出现了一些让学生通过“数学实验——猜想结论——证明结论——利用结论”求解的题目,本题便是典型的一例.在实验探究的过程中,能抓住变化中的等量关系,借助图形的全等进行转化是关键.这样的题目对于培养学生的动手操作能力、猜想发现能力都是非常有益的.
总之,教师应大力加强对《标准》和数学教科书的研究,精心设计教学,结合具体的教学内容,努力把教学内容设计成能引导学生进行观察、实验、分析、比较、联想、类比、归纳的素材,以培养学生的数学猜想意识、猜想习惯、猜想能力,从而培养学生的创新能力.
[1] 李树臣.深入钻研课程标准,努力创提问题情境[J].中学数学,2009(2):1-3.
[2] 李树臣.浅谈数学实验的在教学中的应用[J].中国数学教育,2009(10):15-17.
[3] 李树臣.数学教学过程化的4个常用策略[J].中国数学教育,2010(6):2-5.
[4] 赵绪昌.数学猜想的理性认识与教学思考[J].中学数学杂志,2010(8):1-2.
