由一道考题引出一类二次曲线的等角性质
2011-02-02陈重阳温州中学浙江温州325100
中学教研(数学) 2011年7期
●陈重阳 (温州中学 浙江温州 325100)
由一道考题引出一类二次曲线的等角性质
●陈重阳 (温州中学 浙江温州 325100)
翻阅2011年浙江省普通高中数学会考试卷,其中第41题第(2)小题引起了笔者的兴趣.笔者对该题进行探究后,引出了一类二次曲线的等角性质,供参考.
1 引题
如图1所示,圆C与y轴相切于点T(0,2),与x轴正半轴相交于点N,M(点N在点M的左侧),且|MN|=3.
(1)求圆C的方程.
(2)过点N任作直线与圆O:x2+y2=4相交于点 P,Q,连结 PM,QM.求证:∠PMN=∠QMN.
分析 (2)由已知易得,N(1,0),M(4,0),要证∠PMN=∠QMN,只需证斜率kPM=-kQM,即证kPM+kQM=0,于是可转化为坐标关系
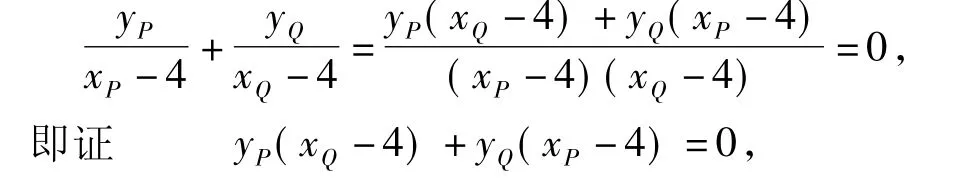
具体求解过程略.
2 激疑
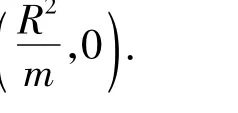
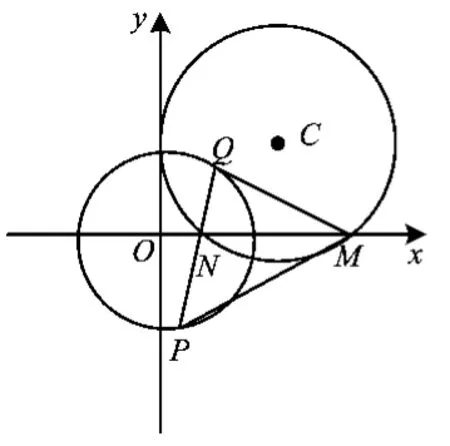
图1
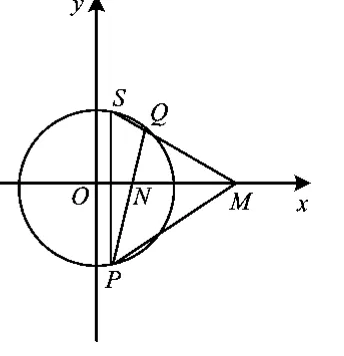
图2
3 追问
在圆锥曲线中是否也有相应的等角性质呢?笔者经过探求,得到以下性质定理.
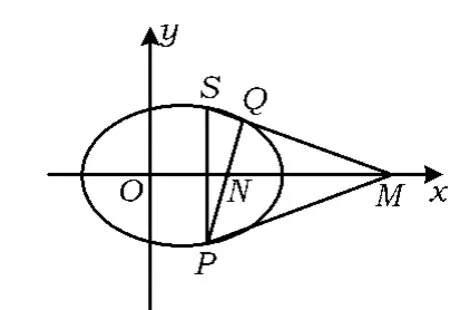
图3

证明设过点N的直线PQ的方程为x=ky+m(k为参变量),则


(3)当 A=F=0,B=1,D= -2p时,二次曲线Γ表示抛物线:y2=2px,此时使等角性质成立的定点是 M(-m,0).
对任意二次曲线,也可通过变换得到相应的性质,这里不再赘述.
[1] 闻杰.圆锥曲线结构思想与解题策略[M].杭州:浙江大学出版社,2010.
