例析二次函数的图象变换
2011-02-01315800浙江省宁波市北仑区顾国和中学
315800 浙江省宁波市北仑区顾国和中学 杨 艳
例析二次函数的图象变换
315800 浙江省宁波市北仑区顾国和中学 杨 艳
图形的平移、轴对称、旋转常见于直线形中,在曲线形——圆中也偶有所见.然而,也有以二次函数图像为背景的图形变换,它的一些性质与直线形的图形变换有许多相通之处.详见下表:
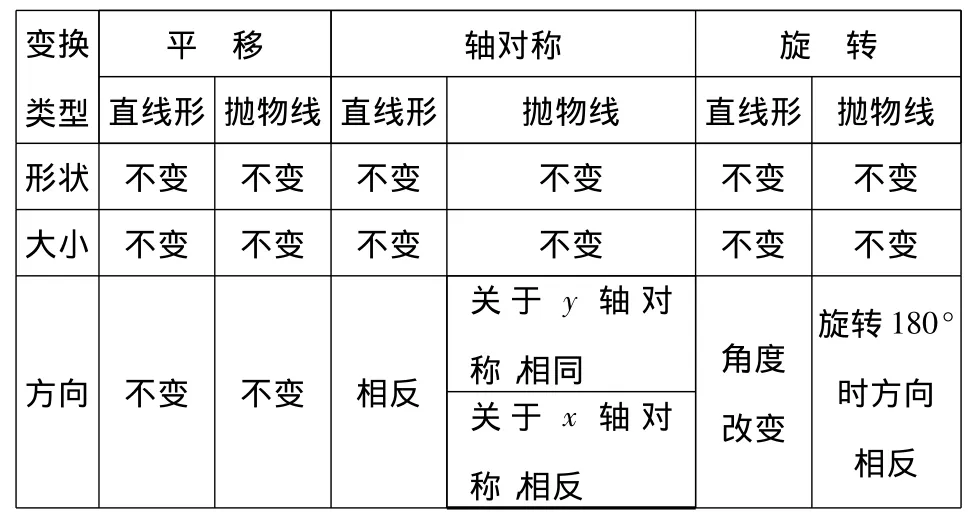
有必要指出,二次函数y=a(x+m)2+k的图象平移、轴对称、旋转时,图象的形状不变,而开口方向要么相同,要么相反,即二次项系数不变,变化的只是它的位置,即关键是顶点(-m,k)位置的改变.对于抛物线的几种变换,可以归结为:一看顶点位置,二看开口方向.
下面例举抛物线的平移、轴对称、旋转问题的求解策略.
1 抛物线的平移
一般地,抛物线的平移有以下规律:
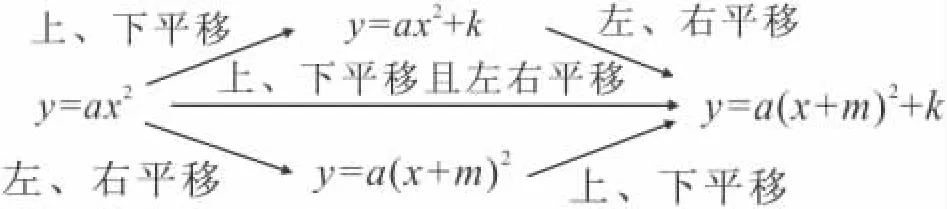
例1 已知抛物线y=x2+2x-3,如何平移此抛物线使其图象与抛物线y=x2-4x+7的图象完全重合.

可知,将抛物线y=x2+2x-3向右平移3个单位,再向上平移7个单位,与抛物线y=x2-4x+7的图象完全重合
.
例2 已知y=2x2的图象是抛物线,若抛物线不动,把x轴,y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是

解析 反其道而行之,即将y=2x2的图象分别向下和向左平移2个单位即可.选B.
2 抛物线的轴对称
我们知道,抛物线y=a(x+m)2+k的顶点坐标为(-m,k),抛物线在对称过程中仅仅是顶点坐标改变,方向相同或相反.由于点(-m,k)关于x轴的对称点为(-m,-k),关于 y轴的对称点为(m,k).所以可得,抛物线y=a(x+m)2+k关于x轴对称(开口方向相反)的图象是y=-a(x+m)2-k,关于y轴的对称(开口方向相同)图象是y=a(x-m)2+k.
例3 作抛物线A关于x轴对称的抛物线B,再将抛物线B向左平移2个单位,向上平移1个单位,得到的抛物线C的函数解析式是y=2(x+1)2-1,则抛物线A所对应的函数表达式是
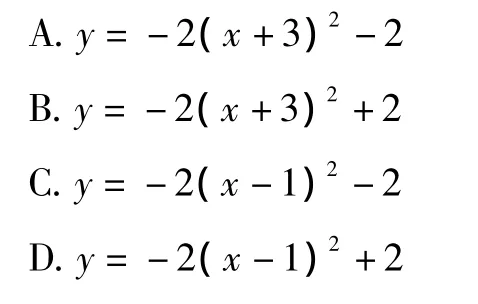
解析 将抛物线C:y=2(x+1)2-1向下平移1个单位,再向右平移2个单位,得抛物线B:y=2(x-1)2-2;再将B关于x轴对称,得抛物线A:y=-2(x-1)2+2.故选 D.
更一般地,抛物线y=a(x+m)2+k关于直线y=e(与x轴平行)对称的抛物线为y=-a(x+m)2+(2ek);抛物线y=a(x+m)2+k关于直线x=f(与y轴平行)对称的抛物线为y=a[(x-(2f+m)]2+k.
3 抛物线的旋转
这里仅讨论抛物线旋转180°的情形.绕某点旋转180°,即关于某点中心对称.已知点(-m,k)关于原点的对称点为(m,-k),所以抛物线y=a(x+m)2+k绕原点旋转180°后所得的抛物线为y=-a(x-m)2-k.
例4 将抛物线y=x2-2x+3绕原点旋转180°,则所得的抛物线的函数解析式为__.
解析 将抛物线y=x2-2x+3化为y=(x-1)2+2,其顶点坐标为(1,2).顶点(1,2)绕原点旋转 180°后为(-1,-2),所以,旋转后的抛物线为y= -(x+1)2-2.
实际上,抛物线的旋转中心不仅限于坐标原点,而具有更一般的规律.(-m,k)关于点(e,f)的中心对称点是(2e+m,2f- k).所以 y=a(x+m)2+k关于点(e,f)的中心对称的抛物线为y=-a[x-(2e+m)]2+(2fk).具体如y=(x-1)2+2关于点(2,3)中心对称所得的抛物线为y=-(x-3)2+4.
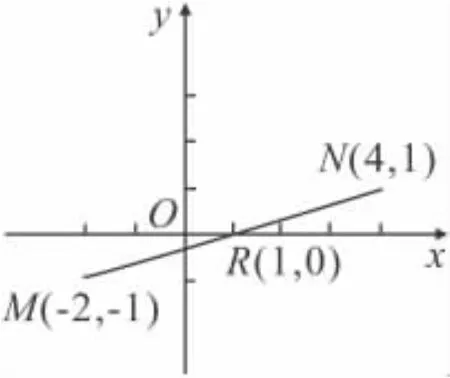
图1
例5 已知二次函数y=ax2+4ax+4a-1的图象是C1.
(1)求 C1关于点 R(1,0)中心对称的图象C2的函数解析式;
(2)设曲线 C1,C2与 y轴的交点分别为 A,B,当,求a的值.
解析 由y=a(x+2)2-1,可知抛物线C1的顶点为M(-2,-1).
由M(-2,-1)关于点 R(1,0)中心对称的点为N(4,1),以 N(4,1)为顶点,与抛物线 C1关于点 R(1,0)中心对称的图象C2也是抛物线,且C1与C2的开口方向相反,故抛物线C2的函数解析式为y=-a(x-4)2+1,即y= -ax2+8ax-16a+1.

综上可见,抛物线的图象变换遵循一般直线形的变换规律,而又有其自身的特点.只有深入理解直线形图形变换的规律和性质,才能在分析抛物线的图象变换时做到有效迁移,求解问题时有的放矢,左右逢源,真正地做到具体情况具体分析,举一隅而三反.
20110311)
