对“再谈梯形与不等式”一文的看法

443300 湖北省宜都市外国语学校 范 鸿

对“再谈梯形与不等式”一文的看法

443300 湖北省宜都市外国语学校 范 鸿

文［1］中，作者对构造一个特殊梯形，直观地解释一组著名不等式，这种创造性的研究精神值得数学爱好者学习.笔者仔细研读，觉得文［1］构造梯形以及求特殊线段的过程较繁琐，并且分一个梯形为两个相似梯形的线段MN是怎样得到的没有讲清楚，只是表达了该线段的客观存在性.笔者发现一个更好的方法去构造这个梯形，也容易求出相应的特殊线段，现提出来供大家交流.

1 构造梯形，求四条特殊线段

构造如图1所示的梯形ABCD，Rt△ABF≌Rt△FCD，AB=CF=a，BF=CD=b，(b＞a).

这是我们再熟悉不过的直角梯形了，美国第二十任总统伽菲尔德(Garfield)曾经用这个梯形证明了著名的勾股定理，也正是通过图1计算四条特殊线段，可以直观地解释这组著名不等式.

以O为圆心，OF为半径作⊙O，与BC，CD分别交于点 E，K.连接 AE，ED，AK.

然后过点E作GE⊥BC，GE分别与AK，AD交于点Q，G，过点O作OH⊥BC于H.

文［1］中，如图2的梯形GEHO中存在平行上下底的线段MN，使梯形EMNG与梯形MHON相似.

2 文［1］中的MN如何作出?

如图3，以 EG和 OH的长之和为直径作⊙T，过 EG和 OH的分点作直径的垂线与⊙T相交，则垂足与交点之间的线段就是EG和OH的比例中项MN.

如图4，为便于说清楚作图的过程，将梯形GEHO从原图中抽取出来.过E任作一条射线，在该射线上依次截取GE=EP，PW=MN(这里MN是图3中的)，

连接WH，过P作PM∥WH交EH于M，过M作GE的平行线交GO于N，

这样完成了在梯形GEHO中作出线段MN，它能使梯形EMNG与梯形MHON相似.

显然，作图的原理是平行线分线段成比例定理.

虽然如此，但笔者觉得上述这样在梯形GEHO中作出MN还是挺麻烦的，需要好几步才能完成.

3 对梯形中两条线段的构成再改进

基于前面的认识，对在图1梯形中构造调和平均值线段、几何平均值线段再改进.

如图5所示，连接图1中梯形ABCD的对角线AC，BD交于点Q，过点 Q作GE⊥BC于E，交AD于点G.再以 H为圆心，以OH的长为半径作圆，交EG的延长线于点R.因为“平行截相似”，所以有:

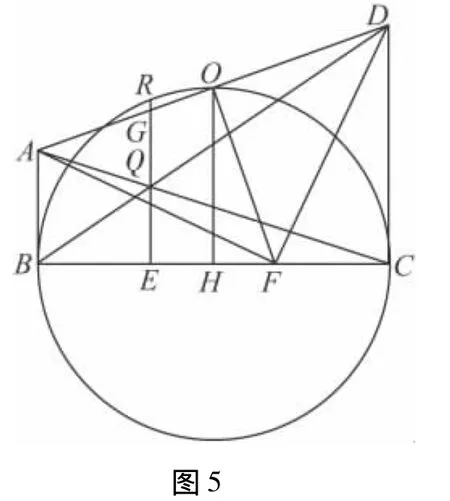
也就是说过梯形对角线交点且平行两底，与两腰相交得到的线段GE是上下底a，b的调和平均值.

由前面1所述，调和平均值线段GE的端点E能分直径BC的两段BE=AB=a，EC=CD=b，

可以看出，在图5中这样构造调和平均值线段GE、几何平均值线段RE要比文［1］中构造GE，MN自然，简单，可操作性强.

1 王凯旋.再谈梯形与不等式［J］.中学数学，2011，3(下)

20110404)

数学茶楼