平面几何中“+=”型问题的新证法

324300 浙江省开化县第二中学 曹嘉兴

324300 浙江省开化县第二中学 曹嘉兴

基本引理 如图1，已知 AB∥EF∥CD，则

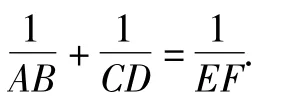
图1

证明 因为AB∥EF∥CD，

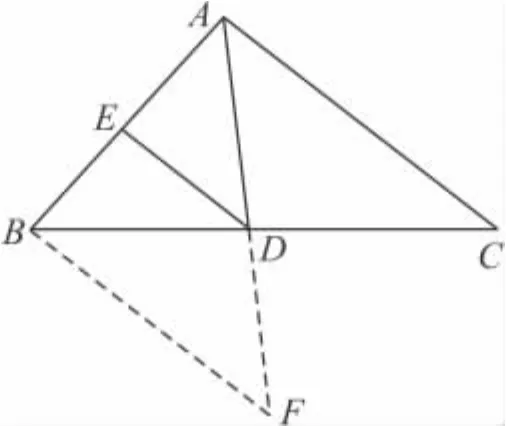
图2

例1 如 图 2，在△ABC中，已知 AD平分∠BAC，DE∥AC交AB于点E.

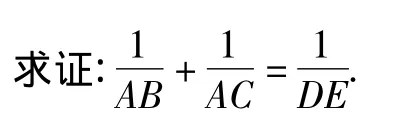
证明 过点B作BF∥DE与AD的延长线相交于点F，因为DE∥AC，所以BF∥AC，于是∠F=∠CAD，又因为

例2 如图3，已知∠POR=120°，OQ 平分∠POR，直线 l分别交 OP，OQ，OR 于 A，B，C.

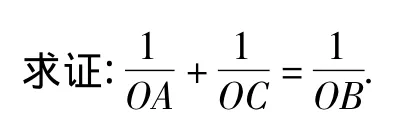
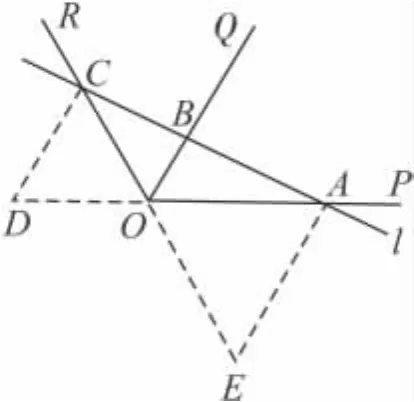
图3

证明 延长AO至点D使OD=OC，延长 CO至点 E使OE=OA，连接 CD，AE.易知△OCD，△OAE均为正三角形，故得CD∥OB∥AE.

例3 如图4，在 Rt△ABC中，⊙O的圆心在斜边AB上，直角边 AC，BC分别切半圆于G，F，⊙O 交斜边 AB 于 D，E.

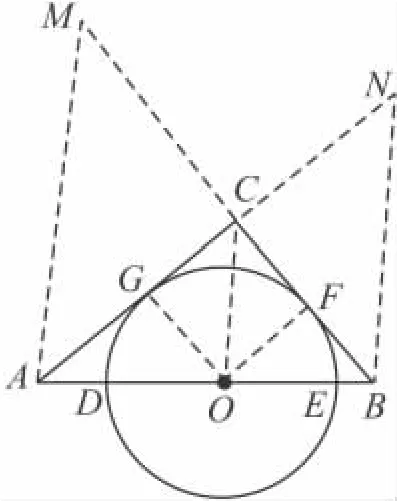
图4

证明 延长BC至点M使CM=AC，延长AC至点N使CN=BC，并连接 AM，BN，OC，OF，OG.易知△ACM，△BCN均为等腰直角三角形，且四边形OFCG为正方形，

故得AM∥OC∥BN.

例4 如图5，△ABC是等腰三角形，过底边BC的中点D任意作一直线l分别交一腰和另一腰的延长线于M，N两点，设AC的中点为E.

图5

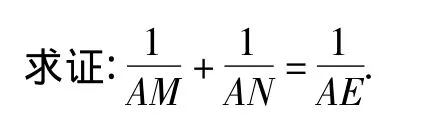
证明 连接DE，过点N作NF∥DE与ME的延长线相交于点F，由三角形的中位线定理可知AB∥DE∥NF.

在“山”字形AMDNFE中，

图6

例5 如图6，在△ABC中，四边形DEFG是△ABC的内接正方形，AM是BC边上的高，高AM分别交 BC，DG 于 M，N.

证明 过点B作BH∥DE与AE的延长线相交于点H，

易知BH∥DE∥AM.

又因为DE=DG，所以BH=BC，又DE=EF，

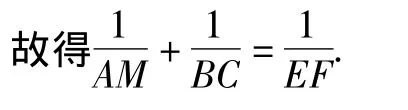
例6 如图7，△ABC是直角三角形，分别以直角边AC，BC为边向形外作正方形 ACDE，BCFG，连接 BE，AG分别交 AC，BC于 R，S.

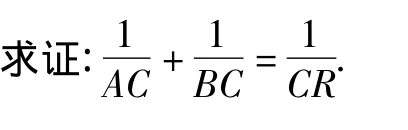
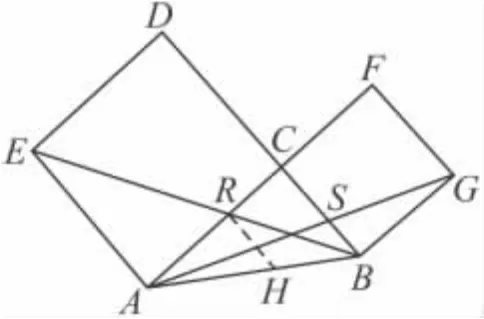
图7

证明 过点R作RH∥BC交AB于点H，易知AE∥RH∥BC.

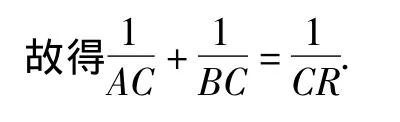
例7 如图8，已知A，B，D三点共线，△ABC，△BDE都是正三角形，连接CD，AE，分别交 BE，BC于G，F.

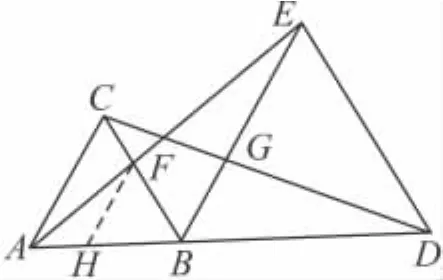
图8

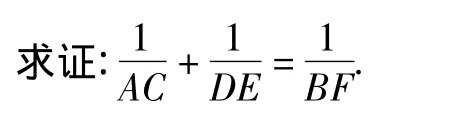
证明 过点F作FH∥AC交AB于点H，

易知AC∥FH∥BE.

在“山”字形CAHBEF中，利用基本引理得

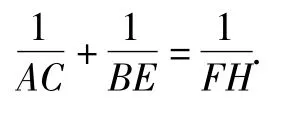
显然△BFH是正三角形，所以FH=BF.

又因为BE=DE，

图9

例8 如图9，在△ABC中，∠A ∶∠B ∶∠C=1 ∶2 ∶4.

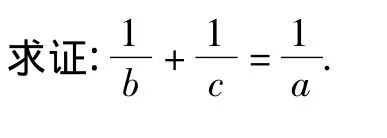
证明 不妨设∠CAB=α，则∠ABC=2α，∠ACB=4α.

在△ABC的内部作∠ACD=α交AB于点D，

则∠CDB=2α =∠ABC，于是 CD=CB=a.

过点B作BE∥CD与AC的延长线相交于点E，

过点A作AF∥CD与BC的延长线相交于点F，

易知∠E=∠ACD=α，∠F=∠DCB=3α=∠ACF，

故得 BE=BA=c，AF=AC=b.显然 AF∥CD∥BE.

在“山”字形FADBEC中，利用基本引理得

20110406)