跷跷板中的几何问题

221000 运河高等师范学校 胡 颖

跷跷板中的几何问题

221000 运河高等师范学校 胡 颖

王娟和张丽正在玩跷跷板，(如图1).这时她们的数学老师走过来，观察一会说:“这个跷跷板中有一个几何问题呢.”

王娟和张丽数学成绩在班里都是名列前茅的，听说有几何题，急忙问:“什么题啊”?老师在他的备课本上一边画一边说出了下面的几何题.

图1

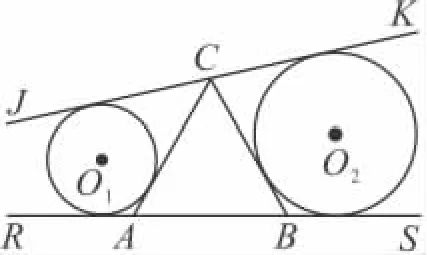
图2

如图2，△ABC为正三角形，过C点任作直线JK(与三角形内部不相交)，过AB作直线 RS，⊙O1与 AR，AC，CJ都相切，⊙O2与 BS，BC，CK都相切，则这两个圆的半径之和是一个定值.王娟看了会说:“我一时看不出为什么是定值，但我知道这个定值就是三角形的高”.张丽问:“为什么啊”?王娟说:“当跷跷板与地面平行时，就看出来了”她画出了图3.老师说:“是啊，其它情形你们回去证证看”.

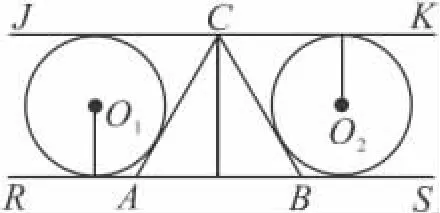
图3

第二天王娟和张丽来找老师，王娟说:“我证出来了，我是这样证的”:如图4

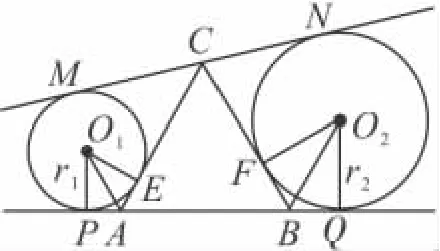
图4

⊙O1与三边的切点记为P，E，M，⊙O2与三边的切点记为Q，F，N，⊙O1的半径记为 r1;⊙O2的半径记为 r2.

设 PA=x，QB=y，AB=1

老师说:“你用的是代数证法，很好”.

张丽说:“我也证出来了，我是这样证的”:如图5

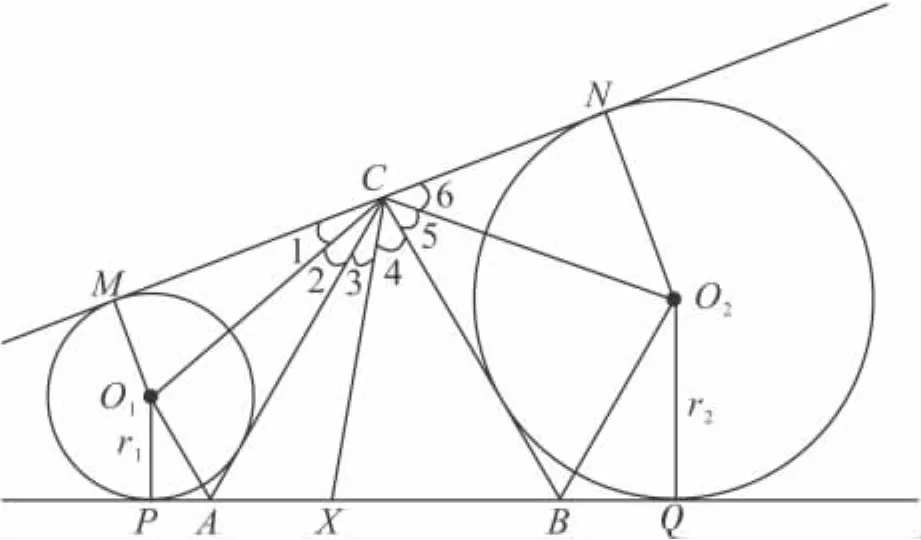
图5

在AB上截取 AX=AO1，又∠CAO1=∠CAX=60°，AC=AC，

老师说:“你用的是几何证法，证法也很巧”.老师接着说:“这里还有一个结论，C点到两个圆心的距离是相等的，你们回去再证证看”.

两个人又高兴地去研究了.

20110323)