地板砖引发的勾股定理万能证明

430079 武汉华中师范大学国家数字化学习工程技术研究中心 彭翕成 张景中

地板砖引发的勾股定理万能证明

430079 武汉华中师范大学国家数字化学习工程技术研究中心 彭翕成 张景中

笔者曾经撰文介绍如何用两个三角形拼摆，得出了勾股定理的多种证法.当然，我们也可以利用计算机，给出勾股定理的多种证法.这种设计来自毕达哥拉斯的启发.

在西方，勾股定理又被称为毕达哥拉斯定理.相传，古希腊数学家毕达哥拉斯是在观察地板图案时发现了勾股定理.由于地板图案都是一样大小的正方形，所以毕达哥拉斯最先发现的是勾股定理对于等腰直角三角形成立(图1).

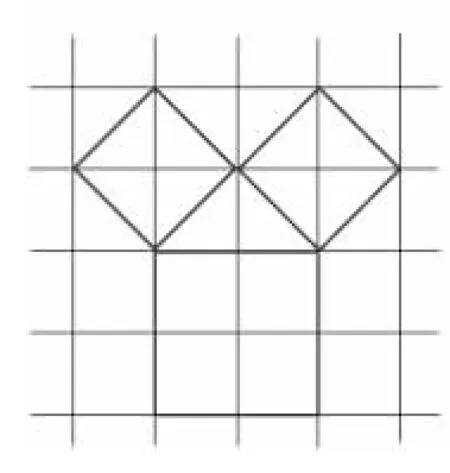
图1

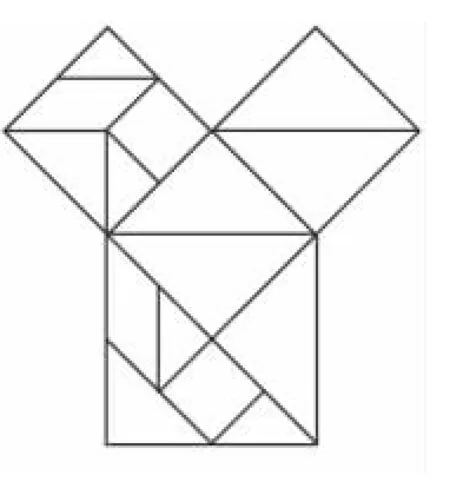
图2

十分巧合的是，我国古代也有类似的图形(图2).不过这个图形不是从地板图案而来，而是将一个正方形纸板分成7份，然后重新进行组合.这算是益智游戏七巧板的一个应用吧.

设计一种地板图案如图3所示，您能从中发现勾股定理么?您若一眼就能看出该图蕴含了勾股定理的三种证法，那就恭喜您有不错的几何直觉!

其实，图中的奥妙远不局限于此.假如设计一种由一大一小正方形铺成的地板，然后我们拿一个正方形纸板(其边长的平方等于原来两个正方形的边长平方和)随手往上一扔，一扔就得到一种证法.扔到特殊位置，面积分割起来就比较简单一点;而扔到一般位置，面积分割起来就需要多一些功夫.

图3

为了更清楚地说明，我们用动态几何软件——超级画板制作了一个课件《勾股定理的万能证明.zjz》.此课件使用很简单，只要拖动屏幕上两个点，就能批量产生勾股定理面积分割证明.大家有兴趣的话，可以到网上去下载，只需在百度上搜索“勾股定理的万能证明”即可.该课件用超级画板打开.

打开课件后，出现界面如图4所示，这本身就是一种证明.为了让演示有序进行，我们先保持红点不变，拖动黄色点，使之从左上方顶点开始，逆时针绕一圈(图5～图16).

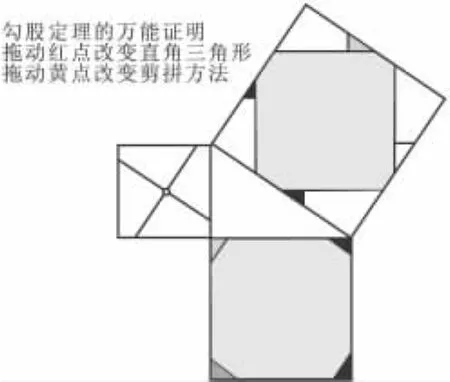
图4

图5(5块)

图6(7块)

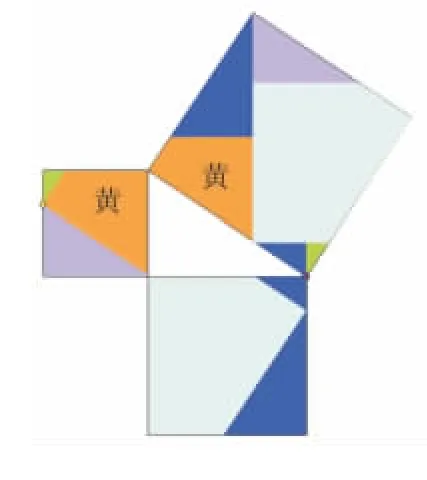
图7(6块)

图8(5块)

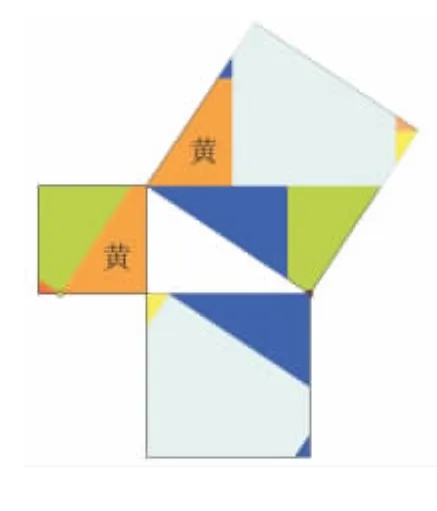
图9(7块)

图10(6块)

图11(5块)

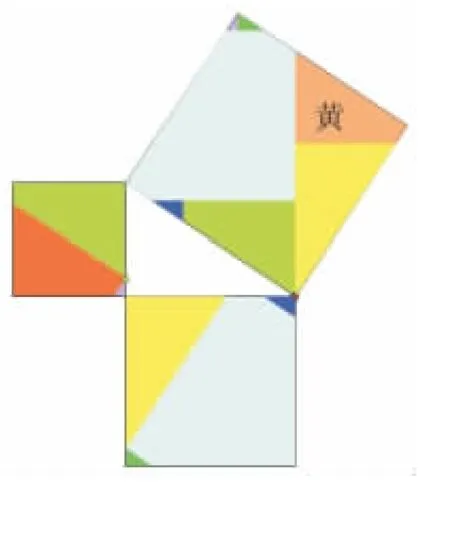
图12(7块)

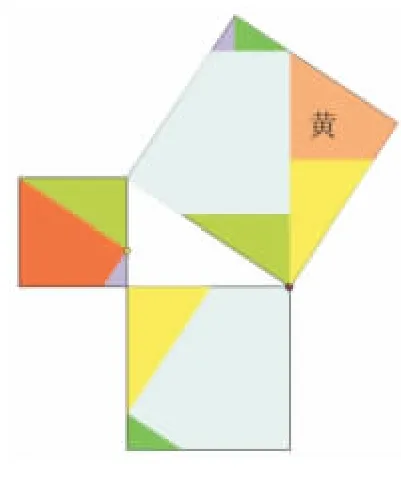
图13(6块)

图14(5块)

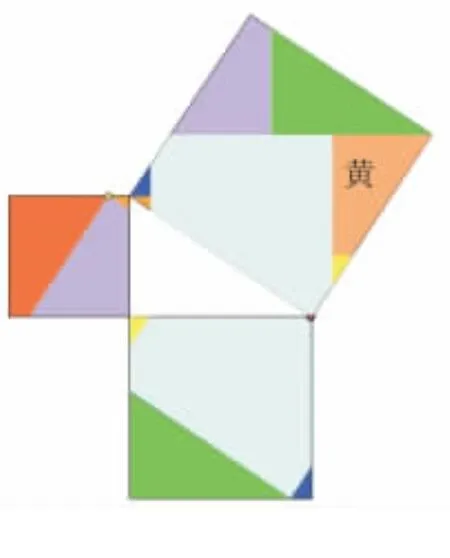
图15(7块)

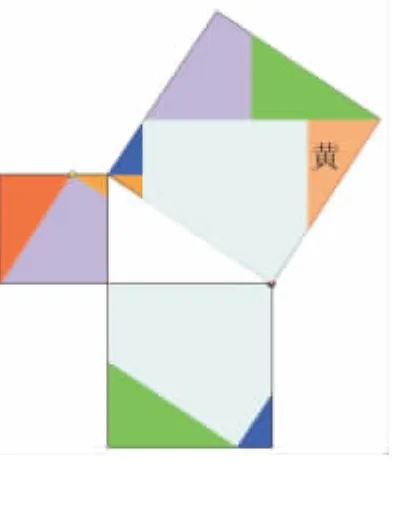
图16(6块)

黄色点在周界上绕完一周后.我们拖动它从左上顶点出发，在内部缓慢移动(图17～图18).

拖动黄色点调整三角形形状，此时黄色点在直角边上较大正方形内.我们仍然从左上方顶点开始拖动黄色点(图19～图21).

图17(7块)

图18(8块)

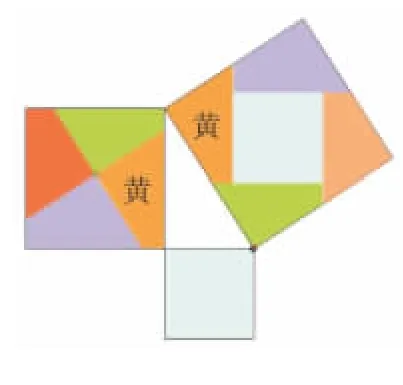
图19(5块)

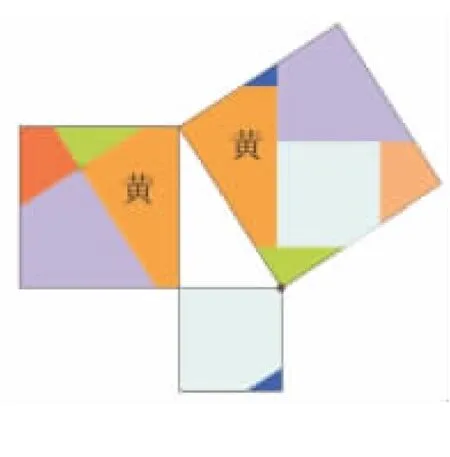
图20(6块)

图21(6块)

图22(6块)

以上只是截取的部分图片，只要有时间，可以得到更多的证明.称之为万能证明，一点都不为过.

以上的变化，都是斜边上的正方形平移作分割.如果考虑旋转则复杂很多，譬如图22的情形可不大容易看出来，还得进一步分割.

勾股定理的证明已经足够多了.多几种、少几种，影响并不大.但利用计算机软件批量生成证明，则是一件很有趣的事情，这也是过去难以想象的.采用先进的技术手段，用探索发现的心态去研究数学，能够看到更多的精彩.

另外，我们也不能忘记是古老的传说故事给予我们的启发，踩在脚下的地板砖看似地位卑微，但却充满智慧.它能给我们灵感，解答我们心中的疑惑.譬如拿破仑定理，从任意三角形三边出发向外作三个等边三角形，而这三个等边三角形的中心构成一个新的等边三角形.这是难倒很多数学爱好者的经典问题.让地板砖来告诉我们怎么做吧.

图23

如图23，假定黑色三角形是最初的任意三角形，以其中一边向外作好等边三角形，再以该等边三角形的中心为旋转中心，将原三角形分别旋转120°和240°，然后以三个非等边三角形向外作等边三角形.这样的操作是可以持续做下去的，直到铺满整个平面.而若我们连接其中的几个中心，就能构造出一个正六边形.这也就得到了拿破仑定理的一个无字证明.

这又给我们启发，单独看某个事物，可能难以看出什么门道.而若将其放之特定环境，从整体来看，很可能就能发现内藏的规律.

20110601)