基于体元分析的三维建筑物模型结构化分割方法
2011-01-31杨必胜李清泉
孙 轩,杨必胜,李清泉,
1.武汉大学遥感信息工程学院,湖北武汉430079;2.武汉大学测绘遥感信息工程国家重点实验室湖北武汉430079
1 引 言
近几年来,建筑物的多尺度(levels of detail, LOD)三维建模逐渐成为了地理信息科学领域探讨的一个新热点[1]。文献[2]提出有效的结构分析有利于在三维多尺度建模中保持建筑物的主要形态特征,但目前却很少有专门针对三维建筑物模型的基本结构和组成进行深入分析和探讨的研究。模型分割作为拓扑关系建立和结构分析最常用的方法[3-4],一直是计算机图形学等相关领域研究的热点[5]。研究有效的建筑物模型结构化分割算法对于建筑物结构分析和提高LOD建模质量具有十分重要的意义。
现有常见的三维模型分割方法主要包括基于曲率特征的方法[6-8]、基于表面元素的方法[9-10]以及面向对象的方法[11-12]三类。然而采用以上方法对建筑物这类结构复杂、细节特征较多的非流形表面对象进行分割,却难以得到理想的结构化分割结果,如图1所示。
针对现有三维模型分割方法在建筑物基本结构特征识别方面存在的不足,本文主要针对建筑物不规则三角网表面模型,从模型内部对其结构组成进行分析,提出了一种基于体元分析的建筑物结构化分割方法。

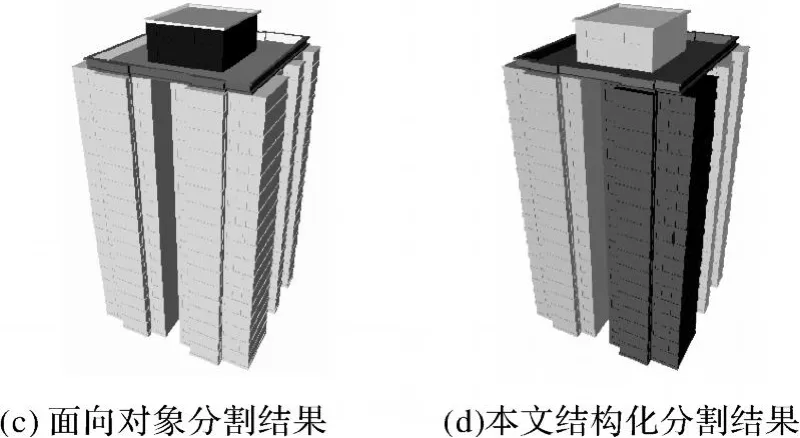
图1 不同算法对建筑物模型分割结果比较Fig.1 Segmentations for 3D building model using different algorithms
2 体元分析与结构化分割
体元分析,是一种将三维对象的表面模型转化为体元模型,并以模型内部各体元的特征参数为基础进行空间分析的方法。该方法不仅可以从三维模型内部对其空间范围进行有效描述,同时能够降低模型表面细节对其整体形状的影响。
考虑到体元分析方法在三维模型分析方面所具有的独特优势,应用提出的结构化分割方法首先对建筑物模型进行体元化,计算所有内部体元与边界体元间的最短距离作为体元特征参数,在三维空间内构建距离场;然后使用局部极值判别方法在距离场内搜索对建筑物结构形状分布具有代表意义的中心体元;按照特定规则依次对中心体元和内、外部体元进行聚类,找到建筑物在空间组成上相互独立的结构单元;最后通过表面投影方式,将体元分析结果扩展到原始模型,得到最终的结构化表面分割结果。算法流程如图2所示。

图2 建筑物模型结构化分割流程Fig.2 Flow chart of structural segmentation of building models
3 分割算法
3.1 距离场计算
由于三维模型的内部距离分布能够有效地反映模型在空间中的形体变化[13-14],选择采用内部距离作为体元分析的基本特征参数,在三维空间中构建基于距离的标量场,简称距离场。
为了满足体元分析需要,采用分层方式分别独立计算各层的水平距离场。其具体步骤如下:
(1)对建筑物模型进行体元化[15],得到模型内部空间的离散化表示,如图3(a)所示。
(2)按照邻域判别方法,对建筑物体元进行基础分类,区分内、外部体元。
(3)依次计算各内部体元到同层所有外部体元间的最短距离,作为该体元的特征参数,并最终形成分层距离场,如图3(b)所示。

图3 建筑物内部分层距离场构建Fig.3 Distance field construction by level in building model
3.2 中心体元提取
为了识别建筑物的基本结构,必须首先提取出对建筑物形状分布具有代表意义的中心体元。
对距离场进行深入分析后发现:距离模型表面较近的体元场值较小,而模型中部体元场值较大。因此在中心体元提取过程中采用了邻域极值判别方法:将当前体元距离参数与其周围二阶邻域内同层体元进行比较,得到局部范围内距离参数最大的体元,作为当前水平体元层的中心体元。如图4所示,灰色方框代表该水平体元层的中心体元。

图4 建筑物水平体元层内中心体元提取结果Fig.4 Midvoxel extraction from horizontal level of building voxels
3.3 体元聚类
体元聚类是建筑物结构化分割的关键。按照算法执行顺序,该过程分为中心体元聚类、内部体元聚类和外部体元聚类三个步骤。
3.3.1 中心体元聚类
中心体元聚类过程包括同层中心体元聚类和不同层中心体元聚合两个步骤。
同层中心体元聚类过程中,一方面对其邻接关系进行考察,另一方面对相邻中心体元的距离场值大小进行比较:由于在各水平体元层中以中心体元为圆心,以距离场值大小为半径的圆形范围反映了建筑物在水平方向上局部区域的大小,从形体变化连续性角度考虑,相互邻接且距离场值变化不大的中心体元被归于建筑物的同一结构单元。如图5(a)所示,不同灰度的方框分别代表了属于不同结构单元的中心体元。
不同层中心体元聚合过程中,本文将相互邻接且距离场值变化具有一定连续性(大小相等、连续递减、连读递增)的上下层中心体元归为同一结构单元。如图5(b)所示,不同颜色方框代表在垂直方向上相互邻接而属于不同结构单元的中心体元,它们依据距离场值变化被聚合为两类。
综合水平聚类与垂直聚类,得到建筑物中心体元的最终聚类结果,如图5(c)所示。
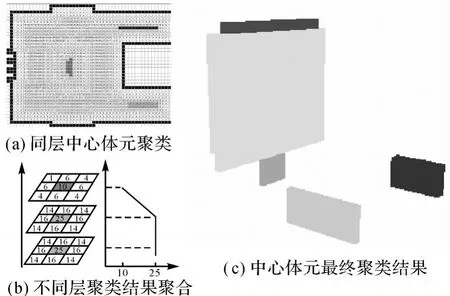
图5 中心体元聚类过程Fig.5 Clustering of midvoxels
3.3.2 内部体元聚类
内部体元聚类的实质是依据中心体元聚类结果,将各水平体元层中的内部体元划归到中心体元所属的不同结构单元中。
以中心体元为参照,距离越近的内部体元越有可能与该中心体元属于同一结构单元。但考虑到建筑物各组成部分本身的形状变化,各内部体元的聚类结果还与其周边中心体元的距离场值大小有关:距离场值越大的中心体元代表了覆盖范围越大的结构单元,属于该结构单元的内部体元可以距离中心体元更远。综合以上两方面因素影响,本文针对内部体元聚类定义了一个影响力参数,用于反映特定中心体元对某内部体元聚类的影响力大小,其计算公式为

式中,v表示内部体元;midt表示类别为 t的某中心体元;Inf(v,midt)表示中心体元 midt对v的影响力;F(midt)表示中心体元 midt的距离场大小;Dist(v,midt)则表示中心体元 midt到 v的水平距离。
按照该公式依次计算各内部体元受到周围所有中心体元影响力的大小,并将其归类到对其影响力最大的中心体元所属类别中,即可得到建筑物内部体元的粗聚类结果,如图6(a)所示。
从内部体元的粗聚类结果来看,虽然大部分内部体元被归入了正确的结构单元,但不同结构单元之间的分类边界并不准确。为了得到准确的内部体元分类结果,通过邻域搜索方法寻找不同结构单元间一定范围内最短的分割直线,并将其作为修正分类边界,对原始聚类结果进行调整,如图6(b)所示,白色线为修正分类边界。

图6 内部体元聚类Fig.6 Clustering of inner voxels
3.3.3 外部体元聚类
外部体元聚类过程主要依据邻域扩张原理,通过对其邻域中内部体元的类别进行判断来实现。
按照从大到小的顺序对外部体元周围水平方向邻接4邻域,水平方向对角4邻域和垂直方向邻接2邻域分别赋予不同的权重(如4、2、1)。通过比较外部体元邻域中各类别的加权和,将其归类到加权和最大的类别中,得到最终建筑物外部体元聚类结果,如图7所示。
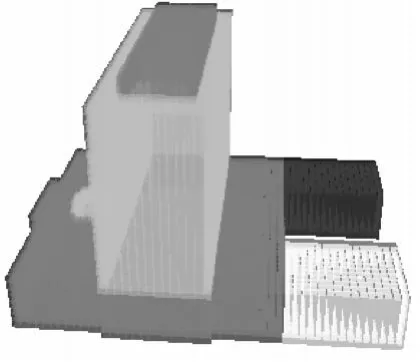
图7 外部体元聚类Fig.7 Clustering of outer voxels
3.4 表面分割
表面分割是建筑物模型结构化分割的最终环节,其关键在于将体元聚类结果投影到原始建筑物表面模型。
对于建筑物的不规则三角网表面模型而言,其表面分割过程首先需要依据邻域判别方法提取出各结构单元间的表面分界线;然后将被分界线穿越的三角形面片分解为较小的面片[16],以解决同一三角形面片属于多个的结构单元的问题;最后通过环分割方法[9]将原始建筑物表面模型划分为相互独立的结构单元,如图8所示。

图8 基于分类边界的三角形面片分解Fig.8 Subdivision of triangular plane place piece based on clustering edge
4 试验与分析
本文选取了一些具有明显时代和地域特征的建筑物进行试验,其模型分割结果如图9所示。从试验结果来看,该算法能够对不同风格建筑物水平和垂直分布的主要结构单元进行有效分割,具有很强的稳健性;另一方面,可看出基于体元分析的结构化分割方法无法对建筑物模型局部的细小结构和表面特征进行有效识别和区分,如欧式建筑屋顶的尖塔、罗马建筑底部的立柱、东方建筑飞檐的纹理等。

图9 各类建筑物结构分割结果Fig.9 Structuralsegmentations ofdifferent styles of buildings
试验基于主频2.0G Intel双核处理器,2G内存的微型计算机平台,对以上各建筑物模型复杂度和分割所用的时间进行统计,得到表1。从表1可以看出,中心提取与体元聚类所需时间与模型复杂度无直接联系,而总分割时间却与模型复杂度正相关。因此随着模型复杂度的提高,模型分割的大多数时间将被用于体元化和表面分割。但由于复杂模型分割所需的整体耗时仍然不大,可见算法运行效率较高。

表1 建筑物模型复杂度与分割时间表Tab.1 Complexity of building models and time costs for segmentation
最后,由于该算法不依赖于模型表面构网方式,在试验中还尝试将其应用于建筑物的点云数据分割(点云数据的表面分割参见文献[17]),也取得了很好的效果,如图10(a)所示。但由于本文体元分析方法的核心在于通过体元聚类对建筑物模型内部空间分布进行有效分析,因此无论何种建筑物模型,都必须具有封闭的外表面;否则将无法确定其内部空间的准确范围,进而产生无效的分割结果,如图10(b)所示。
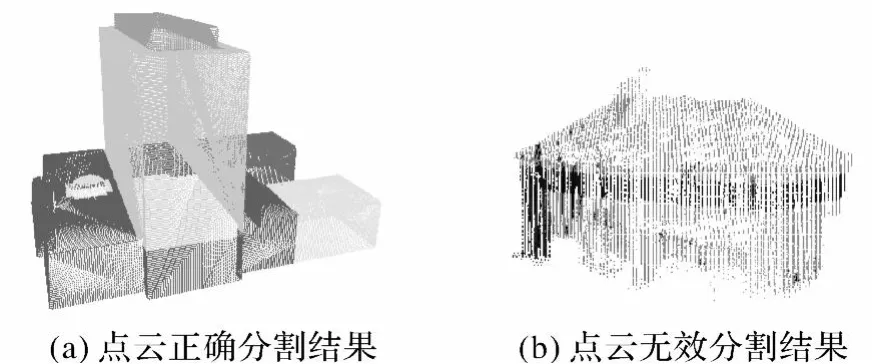
图10 建筑物点云数据分割Fig.10 Segmentation of point clouds of buildings
5 结 语
本文提出的基于体元分析的建筑物模型结构化分割方法能够对建筑物中具有独立意义的主要结构单元进行有效分割,提取出建筑物最基本的形态结构。通过试验验证,该方法与模型表面的构网方式无关,适用于不同风格、不同数据类型三维建筑物模型的分割,具有极强的稳健性,运算效率较高。该方法的不足之处在于无法对建筑物模型局部的细小结构和表面特征进行识别和分割,并要求建筑物模型具有封闭的外表面。
进一步将研究建筑物三维模型的多尺度结构化分割,并基于建筑物结构化分割结果,探讨在包括建筑物LOD建模在内的各类建筑物三维数据处理过程中保持建筑物基本结构特征的有效方法。
[1] ZHU Qing,HU Mingyuan.Semantics-based LOD Models of 3D House Property[J].Acta Geodaetica et Cartographica Sinica,2008,37(4):514-520.(朱庆,胡明远.基于语义的多细节层次3维房产模型[J].测绘学报,2008,37(4): 514-520.)
[2] MENG Liqiu,FORBERG A.3D Building Generalization [C]∥Challenges in the Portrayal of Geographic Information:Issues of Generalisation and Multi Scale Representation.Amsterdam:Elsevier Science,2007:211-232.
[3] HOFFMAN D D,RICHARDS W A.Parts of Recognition [J].Cognition,1984,18(3):65-96.
[4] AL EKSEY G,THOMAS F.Randomized Cuts for 3D Mesh Analysis[C]∥Proceedings of ACM SIGGRAPH Asia’08.New York:ACM,2008:145-156.
[5] SHAMIR A.A Survey on Mesh Segmentation Techniques [J].Computer Graphics Forum,2008,27(6):1539-1556.
[6] LAVOUE G,DUPONT F,BASKURT A.A New CAD Mesh Segmentation Method Based on Curvature Tensor Analysis[J].Computer Aided Design,2005,37(10):975-987.
[7] PAGE D,KOSCHAN A,ABIDI M.Perception-based 3D Triangle Mesh Segmentation Using Fast Marching Watersheds[C]∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Los Alamos:IEEE Computer Society Press,2003:27-32.
[8] KATZ S,TAL A.Hierarchical Mesh Decomposition Using Fuzzy Clustering and Cuts[C]∥Proceedings of ACM SIGGRAPH.New York:ACM,2003:954-961.
[9] LU Y,GADH R,TAUTGES T J.Feature Based Hex Meshing Methodology:Feature Recognition and Volume Decomposition[J].Computer-Aided Design.2001,33(3): 221-231.
[10] THIEMANN F,SESTER M.Segmentation of Buildings for 3D-Generalisation[C]∥ICA Workshop on Generalisation and Multiple Representation. Leicester: [s. n.],2004.
[11] ATTENE M,FALCIDIENO B,SPAGNUOLO M.Hierarchical Mesh Segmentation Based on Fitting Primitives [J].The Visual Computer,2006,22(3):181-193.
[12] SIMARI P,KALO GERA KIS E,SIN GH K.Folding Meshes:Hierarchical Mesh Segmentation Based on Planar Symmetry[C]∥Proceedings of Eurographics Symposium on Geometry Processing.New York:ACM,2006:111-119.
[13] WADE L,PAREN T R E.Automated Generation of Control Skeletons for Use in Animation[J].The Visual Computer,2002,18(2):97-110.
[14] WANGJiale,HE Yuanjun,TIAN Haishan.Voxel-based Shape Analysis and Search of Mechanical CAD-Models [J]. Forschung im Ingenieurwesen,2007,71(4): 189-195.
[15] FANG Shiaofen,CHEN HongSheng.Hardware Accelerated Voxelization[J].Computers&Graphics.2000,24(3): 433-442.
[16] FOUMIER A,MONTUNO D Y.Triangulating Simple Polygons and Equivalent Problems[J].ACM Transaction on Graphics,1984,3(2):153-174.
[17] ADAN A,HUBER D.Reconstruction of Wall Surfaces under Occlusion and Clutter in 3D Indoor Environments [R].Pittsburgh:Robotics Institute,Carnegie Mellon University,Tech.Rep.CMU-RI-TR-10-12,2010.
