基于切割环分解的三维建筑物细节层次模型构造
2011-12-25杨必胜姜少波
杨必胜,姜少波
1.武汉大学测绘遥感信息工程国家重点实验室,湖北武汉430079;2.武汉大学时空数据智能获取技术与应用教育部工程研究中心,湖北武汉430079
基于切割环分解的三维建筑物细节层次模型构造
杨必胜1,2,姜少波1,2
1.武汉大学测绘遥感信息工程国家重点实验室,湖北武汉430079;2.武汉大学时空数据智能获取技术与应用教育部工程研究中心,湖北武汉430079
提出一种基于切割环分解的建筑物LOD(细节层次)模型的自动生成方法,该方法首先通过二面角操作算子识别建筑模型中的切割环,然后通过切割环将建筑物模型迭代分割成建筑主体和一系列细部特征,并将分割的结果存储在一棵构造实体几何树(CSG tree)中,最后对特征部件按重要性进行等级划分,同时进行简化处理。试验结果表明该方法具有较高的计算效率,能有效减少模型表面的细节和较好保持模型的结构特征。
3D建筑物模型;模型分解;切割环;CSG树;特征识别
1 引 言
三维城市模型(3D city models,3DCM)作为城市的三维逼真描述,在城市建设和规划等相关领域得到广泛应用。由于不同的应用对三维城市模型具有不同细节层次需求,因此需要对三维城市模型进行细节层次(levels of detail,LOD)表达,从而满足海量三维城市模型数据的交互式实时可视化、网络渐进传输等方面的需求[1-4]。建筑物LOD模型自动生成的关键是通过模型简化或综合等操作算子生成一系列从精细到粗糙的建筑物模型。计算机图形学领域已经开发许多比较成熟的三维模型简化算法[5],这些算法一个共同特点是通过几何元素删除法或基于小波变换的方法实现三维模型从细到粗的LOD表达。这些方法对三维自由平滑曲面模型十分有效,尤其在地形LOD模型的自动生成方面具有很好的效果[6-8]。建筑物模型在整体几何结构上主要是由平面构成,面和面之间具有明确的几何约束关系,如共面、平行、垂直相交和对称等[9],而且不存在高冗余度的几何细节(图1(a));其次,建筑物模型中存在大量的具有内在几何关系约束的语义部件,如:门、窗、阳台、烟囱和屋顶等,目前针对三维自由曲面的简化算法如文献[10]中的Qslim,均难以保持建筑物模型自身固有的特征和约束,如图1(b)。
近年来,三维建筑物的简化引起许多学者的关注。文献[11—12]提出一种平面分割方法,建筑物首先被分割成一些特征部件,然后对其进行分析综合,该方法需要应用很多分割平面,算法比较复杂;文献[9,13—14]采用一种半空间剖分的方法,该方法对于在不同层具有不同几何结构的建筑物难以奏效;文献[15]基于尺度空间理论利用开运算和闭运算移除小的部件和填补小的空洞,该算法仅适合于正交平行结构的建筑物;文献[16]提出一种感知驱动的简化方法,但需要将三维模型转化成二维影像提取感知信息,计算代价比较大;文献[17]提出一种人造对象间断式的简化方法,对比较简单的人造模型能够取得较好的效果,但对于稍微复杂的特征部件难以识别;文献[18]对各种3D建筑物的简化和综合方法进行了比较分析。

图1 Qslim简化建筑物模型的效果Fig.1 Simplification effect of a building model with Qslim
综上所述,现有简化算法难以有效处理建筑物模型的LOD生成,因此提出一种基于切割环分解的建筑物模型简化方法。首先通过二面角操作算子识别建筑模型中的切割环,然后通过切割环将建筑物模型迭代分割成建筑主体和一系列部件,同时将分割的结果存储在一棵构造实体几何树中,最后对相应的部件进行简化,从而生成三维建筑物的LOD模型。
2 基于切割环的建筑物LOD模型生成
2.1 三维建筑物模型的描述
由于三维场景中,建筑物整体结构大多规则简单,而表面结构特征比较复杂,因此在研究中,只针对由三角网平面片构成的二维流形拓扑模型,暂时不考虑具有自由曲面的实体模型,对于由很多不连通的部件组成的三维建筑模型,在简化的过程中不会改变其拓扑关系。建筑物模型的最小表达单元是三角形。因此,对于建筑物模型M可以表达为

式中,V是三维空间内的点,具有确定几何坐标。
显然,建筑物模型的最小表达单元中三角形的任意2个顶点〈Vi,Vj〉构成一条边 ek=〈Vi, Vj〉。为描述方便,定义四个概念:①凸边,从模型的外部进行观察,该边相邻的两个三角形的二面角大于180°,如图2(a);②凹边,从模型的外部进行观察,该边相邻的两个三角形的二面角小于180°,如图2(b);③平面边,该边相邻的两个三角形共面;④切割环,如果某个封闭环能将建筑物模型分割为两个面壳,而且每个面壳的体积不为0,则该封闭环被定义为切割环,切割环上的边称为切边,面壳填洞后对应的实体称为分割体。
图3(a)中的环l1分割模型后得到两个面壳,其中有一个面壳 FS1为平面片,体积为0,因此环l1不是切割环。根据切边的凹凸性,选择三类切割环进行分割:①凹切割环,切割环中的所有切边都是凹边;②凸切割环,切割环中的所有切边都是凸边;③混合凹切割环,切割环中的切边由凹边和平面边组成,且该环的所有切边在一个平面内。图3(b)中l2为凹切割环,图3(c)中 l3为凸切割环,图3(d)中 l4为混合凹切割环,它由黑色表示的凹边和灰色表示的平面边组成。

图2 凸边和凹边Fig.2 Convex edge and concave edge

图3 切割环举例Fig.3 Illustration of cutting loops
文献[19]认为三维模型中的特征是一些能够从原始模型中有效分离出来的连接区域。对于建筑物模型而言,其表面结构特征主要表现为突出和凹陷的部件,如窗户、门、阳台、烟囱等,这些部件可以看成原始模型的一个子集,其可以任意复杂,但能从原始模型中有效分离,如图4。由于切割环是分离建筑主体和特征部件的分界线,因此,识别建筑物模型中存在的切割环是实现建筑物LOD模型自动生成的关键步骤。
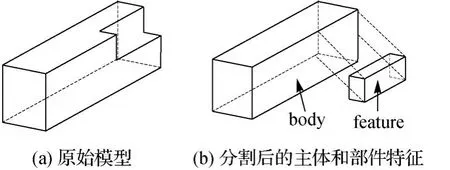
图4 建筑物模型的结构特征Fig.4 Structural feature of a building model
2.2 切割环的识别
根据切割环的特性,提出基于切割环分解的三维建筑物LOD模型的生成方法,该方法的主要步骤如图5。

图5 算法流程图Fig.5 The workflow of algorithm
为实现建筑物模型中切割环的自动识别,提出一种基于边的深度优先搜索(DFS)方法,为提高搜索效率,采用一种带方向的半边数据结构[20],切割环的识别过程是一种递归的半边遍历过程,主要包括凸凹切割环和混合凹切割环的识别。
凸凹切割环识别:①标记凸凹边集合中的所有边为未遍历;②选取边集合中的一条未遍历边为种子边,设为e1,标记e1为遍历标志;③递归遍历e1的未被遍历的邻接边 en,en与e1具有相同的凸凹性,标记 en为遍历标志;④重复步骤③,记录找到的封闭环;⑤如果找到的环满足切割环的定义,则该环为凸凹切割环;⑥转跳到步骤②,直到所有的凸凹边均被遍历。
混合凹切割环由凹边和平面边组成,其识别过程主要分为两步:找到一条不封闭的凹边集合;检测平面边集合,将不封闭的凹边集合封闭起来,构成一个切割环。其中第一步与凸凹切割环的识别类似,在此不再赘述。在第二步中,如果平面边集合属于模型上的边,则根据混合凹切割环的定义很容易判断,如图3(d)中的灰色边;如果平面边集合不属于模型上的边,则需要沿着凹边集合的延伸方向生成平面边集合,如图6。文献[21]针对CAD模型提出一种基于自然扩展生成平面边的方法,该方法比较复杂。针对建筑物的结构特征,改进平面边的生成方法。
设不封闭凹环集合 l={e1,e2,…,en},若 n> 1,则以l所在的平面作为分割平面对模型进行分割,产生的交线即为平面边集合。若n=1,设e的两个邻面分别为 f1和 f2,如图6,首先以 f1为分割平面对模型进行分割,设分割体中特征部件的最小外包体积为V1;同理以 f2为分割平面得到特征部件的最小外包体积为V2。如果V1 图6 平面边的生成Fig.6 Generation of planar edges 通过以上切割环的检测可以识别出三维建筑物模型中的三类切割环,由于不同类型的切割环可能存在相交的情况,这样会导致同一个结构模型的多种分割方式,如图7所示。因此对于相交的切割环,必须舍弃那些导致分割质量不好的切割环,仅保留一个分割质量最好的切割环。文献[11]采用分割面上的新面积与旧面积的比值评价分割质量,对于有些模型,如其特征部件的新面积较大而体积很小,这种标准可能不太适合,因此,采用分割体的最小外包体积比值作为分割质量标准进行切割环的取舍。 式中,VF为特征部件的最小外包体积,VB为主体的最小外包体积。Q的值越小,则分割质量越好,相应的切割环被认为是越好的切割环,保留最小Q值所对应的切割环。图7说明具有相交关系的混合凹切割环l1和凸切割环 l2所导致的两种分割方式,其中加性分割用布尔并操作∪表示,减性分割用差操作∩表示,设l1和l2对应的分割质量分别为Q1和Q2,由于Q1>Q2,因此切割环l1被舍弃,保留切割环l2。通过切割环的取舍可以得到用于模型层次分割的切割环集合L。 图7 一种结构模型的两种分割方式Fig.7 Two different partitions of a model 从建筑物模型中识别出的切割环即是建筑物主体与部件的分割线。给定建筑物模型M和一条切割环l,沿着l进行裁剪可以将建筑物模型分割成两个面壳M1、M2。 根据切割环集合L,建筑物模型M能被分割成主体和一系列部件特征,因此,可以用一颗具有二叉结构的CSG树予以表达。为了使得构建的二叉树尽量平衡,必须建立切割环集合L={l1, l2,lopt,…}中各切割环之间的层次关系,采用分割准则ΔV确定切割环的层次。假设切割环集合L中的某条切割环l将建筑物模型M分割成两个部分M1、M2,相应的最小外包体积为V1和V2,若ΔV=|V1-V2|=min,则该环被确定为分割模型M的最优切割环,设为lopt,将相应的两个分割体M1、M2存储于CSG树的左右节点上,同理,对节点M1、M2进行分割,根据分割准则可以确定M1、M2的最优切割环,设为 l1、l2,由于 M和M1、M2具有层次关系,因此对应的最优切割环 lopt和 l1、l2也具有相应的层次关系,依此类推,直到确定所有切割环的层次关系为止,从而构造出一颗平衡CSG树。显然,如下层次分割是一种递归的过程。 为方便起见,构造CSG树时将特征部件存储为左节点,主体存储为右节点,图8描述了分割结果的实例。 图8 模型分割结果的CSG树Fig.8 Partitioning of a model into a CSG tree 原始建筑物模型经过切割环的分割后变为一颗具有二叉结构的CSG树,通过对CSG树的叶节点进行删除或简化,可以生成建筑物的LOD模型。如何选择需要简化的部件,即特征部件在给定尺度下如何进行重要性排序成为重要的问题,为此定义每个叶节点的代价函数为 式中,V为原始模型M的最小外包体积;Vi为特征部件Mi的最小外包体积。根据代价函数计算CSG树中每个叶节点的代价,代价开销最小的叶节点将优先被简化或删除。建筑物LOD模型的生成步骤为:①节点删除,选择C值最小的的左孩子叶节点Mi,将该节点删除并作删除标记,同时对相应的右孩子节点进行填洞和共面处理,并将结果存储在左孩子节点上;②节点收缩,如果一个节点的左孩子节点被标记为删除,且右孩子节点为叶子节点,则这两个孩子节点可以收缩成一个父节点,并将左孩子节点的内容存储在父节点上。 经过上面处理后,CSG树中所有叶子节点的组合将形成一个有效的LOD,通过设置代价阈值T,可以生成不同层级的LOD模型。图9说明了节点M1的简化过程。 图9 CSG树中节点M1的简化Fig.9 Simplification of nodeM1in CSG tree 其中,需要说明的两个操作为:①填洞处理,如果一个面壳节点的切割环的所有切边共面,直接对该环采用多边形三角化方法即可,如果所有切边不在一个平面内,作者采用切割环在面上的收缩方式来进行填洞[22],首先在面壳中寻找切割环的邻接面,然后将这些邻接面自然向外延伸并相交,即可将空洞填补;②共面处理,填洞处理后,模型中可能存在许多冗余的共面三角形,选择文献[10]的方法,指定一个接近于0的阈值 Tc进行处理,Tc通常取1.0×10-4。 在Windows XP3平台下采用C++和Open-GL相结合实现了本文提出的算法,为检验该算法在LOD模型生成方面的效果,选取了四组不同的现代建筑物模型进行试验,表1列出试验数据与试验条件的基本信息。 表1 试验数据与试验条件Tab.1 Experimental data and conditions 根据该算法,通过选取不同的阈值 T,分别对四组试验数据生成了三层LOD模型,并和多分辨率生成算法Qslim在相同的简化率下进行比较,见图10~图13,其中LOD0表示原始模型。图10中,LOD1模型的三角形数量为52,LOD2模型的三角形数量为12;图11中,LOD1模型的三角形数量为924,LOD2模型的三角形数量为404;图12中,LOD1模型的三角形数量为1 749, LOD2模型的三角形数量为270;图13中,LOD1模型的三角形数量为2 514,LOD2模型的三角形数量为540。本文方法所产生的LOD模型较好的保持建筑物模型的整体结构特征,而Qslim方法所产生的LOD1基本上保持建筑物的整体结构特征,但LOD2出现明显的变形,破坏建筑物的平行、对称性等特征。 图10 本文算法和QSlim生成建筑物LOD的比较(data-1)Fig.10 Comparison of LOD models obtained with our algorithm and Qslim(data-1) 图11 本文算法和QSlim生成建筑物LOD的比较(data-2)Fig.11 Comparison of LOD models obtained with our algorithm and Qslim(data-2) 图12 本文算法和QSlim生成建筑物LOD的比较(data-3)Fig.12 Comparison of LOD models obtained with our algorithm and Qslim(data-3) 图13 本文算法和QSlim生成建筑物LOD的比较(data-4)Fig.13 Comparison of LOD models obtained with our algorithm and Qslim(data-4) 由模型生成LOD模型的运行时间见表2,本文算法运行时间在1.0 s左右,具有较高的效率。 表2 本文算法效率评价Tab.2 Algorithm efficiency evaluation s 本文方法通过切割环识别建筑物模型表面的结构特征,从而实现建筑物模型的分割,进而在保留建筑物整体结构特征的前提下实现建筑物模型的简化。试验的结果和与现有的简化方法的比较表明该方法能够有效地实现切割环的识别并对建筑物模型进行分割,从而保证生成的建筑物LOD模型能够保持其整体的结构特征。该方法只适合于三角网平面片组成的建筑模型,因此,本研究的下一步将重点解决具有自由曲面特征的建筑物模型,并对生成的LOD模型进行定量分析实现LOD模型间的相似性度量。 [1] GLANDER T,DOLLNER J.Abstract Representations for Interactive Visualization of Virtual 3D City Models[J]. Computers,Environment and Urban Systems,2009,33 (5):375-387. [2] ZHU Qing,HU Mingyuan.Semantics-based LOD Models of 3D House Property[J].Acta Geodaetica et Cartographica Sinica,2008,37(4):514-520.(朱庆,胡明远.基于语义的多细节层次3维房产模型[J].测绘学报,2008,37(4): 514-520.) [3] PONCHIO F,HORMANN K.Interactive Rendering of Dynamic Geometry[J].IEEE Transactions on Visualization and Computer Graphics,2008,14(4):914-925. [4] YAN G B S,LI Q Q,GONG J Y.A Robust and Rapid Algorithm for Generating and Transmitting Multiresolution Three Dimensional Models[J].Chinese Science Bulletin, 2006,51(8):987-993. [5] LUEBKE D,REDDY M,COHEN J,et al.Level of Detail for 3D Graphics[M].San Francisco:Morgan Kaufmann, 2003:19-46. [6] YANGB S,LI Q Q,SHI W Z.Constructing Multiresolution Triangulated Irregular Network Model for Visualization[J].Computers and Geosciences,2005,31(1):77-86. [7] YANG B S,SHI W Z,LI Q Q.A Dynamic Method for Generating Multiresolution TIN Models[J].Photogrammetric Engineering and Remote Sensing,2005,71(8): 917-927. [8] PAJAROLA R,GOBBETTI E.Survey of Semi-regular Multiresolution Models for Interactive Terrain Rendering [J].The Visual Computer,2007,23(8):583-605. [9] KADA M.Scale-dependent Simplification of 3D Building ModelsBased on CellDecomposition and Primitive Instancing[C] ∥ Proceedings of the International Conference on Spatial Information Theory.Melbourne: Springer Verlag,2007:222-237. [10] GARLAND M,HECKBERT P.Surface Simplification Using Quadric Error Metrics[C]∥SIGGRAPH Proceedings.Los Angeles:Addison Wesley,1997:209-216. [11] THIEMANN F,SESTER M.Segmentation of Buildings for 3D Generalisation[C]∥Proceedings of ICA Workshop on Generalisation and Multiple Representation.Leicester: [s.n.],2004:1-7. [12] THIEMANN F,SESTER M.3D-symbolization Using Adaptive Templates[C]∥Proceedings of ISPRS Technical Commission Symposium.Vienna:[s.n.],2006:109-113. [13] KADA M.3D Building Generalization Based on HalfspaceModeling[C] ∥Proceedingsofthe ISPRS Workshop on Multiple Representation and Interoperability of Spatial Data.Hannover:[s.n.],2006:58-64. [14] KADA M.Generalization of 3D Building Models for Map-like Presentations[C]∥The International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences:XXXVII.[S.l.]:ISPRS,2008: 399-404. [15] FORBERG A.Generalization of 3D Building Data Based on a Scale-spaces Approach[J].ISPRS Journal of Photogrammetry and Remote Sensing,2007,62(2):104-111. [16] DU Z Q,ZHU Q.ZHAO J Q.Perception-driven Simplification Methodology of 3D Complex Building Models[C]∥The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences:XXXVII.[S.l.]:ISPRS,2008:645-651. [17] JANGJ,WONKA P,RIBARSKY W,et al.Punctuated Simplification ofMan-made Objects[J]. TheVisual Computer,2006,22(2):136-145. [18] SESTER M.3D Visualization and Generalization[C]∥51st Photogrammetric Week.Stuttgart:[s.n.],2007: 285-295. [19] RIBELLES J,HECKBERT P S,GARLAND M,et al. Finding and Removing Features from Polyhedra[C]∥Proceedings ASME Design Engineering Technical Conference.Pittsburgh:[s.n.],2001:1-10. [20] BOTSCH M,PAUL Y M,ROSSL C,et al.Geometric Modeling Based on Triangle Meshes[C]∥Proceedings of ACM SIGGRAPH 2006 Courses.New York:ACM, 2006:26-27. [21] LU Y,GADH R,TAUTGES T J.Feature Based Hex Meshing Methodology:Feature Recognition and Volume Decomposition[J].Computer-aided Design,2001,33(3): 221-232. [22] MA L J,HUANG Z D,WU Q S.Extracting Common Design Patterns from a Set of Solid Models[J].Computer-Aided Design,2009,41(12):952-970. Generating Levels of Detail of 3D Building Models Based on Cutting Loops Decomposition Y ANGBisheng1,2,J IANG Shaobo1,2 A cutting loop decomposition approach for generating LOD of 3D building models was proposed.Firstly, the cutting loops of 3D building model were detected according to a dihedral angle operator.Secondly,the building model was decomposed into the main body and a series of feature parts through the cutting loops,which were stored as nodes in a CSG tree.Finally,the nodes in the CSG tree were selectively simplified according to the significance of each node.The experimental results show that the proposed approach is efficient and able to preserve the structural features of the building models. 3D building models;model decomposition;cutting loop;CSG tree;feature identification Y ANG Bisheng(1974—),male,professor, PhD supervisor,majors in geoinformatics,lidar point clouds understanding and mapping,multi-scale modeling and progressive transmission of spatial data. 1001-1595(2011)05-0575-07 P208 A 教育部新世纪优秀人才支持计划(NCET-07-0643);教育部重点项目(108085);中央高校基本科研业务费专项资金(3103005) (责任编辑:宋启凡) 2010-06-17 2010-10-14 杨必胜(1974—),男,教授,博士生导师,主要从事激光扫描点云解译与三维重建、空间数据的多尺度建模与渐进传输方面的研究。 E-mail:bshyang@whu.edu.cn


2.3 基于切割环的建筑物模型层次分割


2.4 建筑物LOD模型生成

3 试验结果






4 结 论
1.State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University,Wuhan 430079, China;2.Engineering Research Center for Spatio-temporal Data Smart Acquisition and Application,Ministry of Education of China,Wuhan University,Wuhan 430079,China
