基于SIFT的宽基线立体影像密集匹配

杨化超,姚国标,王永波

1.国土环境与灾害监测国家测绘局重点实验室,江苏 徐州 221116;2.中国矿业大学 环境与测绘学院,江苏 徐州221116

基于SIFT的宽基线立体影像密集匹配

杨化超1,2,姚国标2,王永波1,2

1.国土环境与灾害监测国家测绘局重点实验室,江苏 徐州 221116;2.中国矿业大学 环境与测绘学院,江苏 徐州221116

提出基于对极几何和单应映射双重约束及SIFT特征的宽基线立体影像多阶段准密集匹配算法。算法包括三个阶段:①基于特征点的空间分布和信息熵选取一定数量的最优SIFT特征点集并进行最小二乘初始稀疏匹配及立体像对的基本矩阵和单应矩阵估计;②对于其余特征,利用同名核线倾斜角及SIFT特征的尺度信息对匹配窗口的仿射变换参数进行迭代优化及变形改正、提取仿射不变SIFT特征描述符,并基于双重约束信息及欧氏距离测度进行匹配;③考虑宽基线立体影像较低的特征提取重复率,对第②步左右影像中未能成功匹配的特征点,基于双向搜索策略,采用基于盒滤波加速计算的SSD测度在变形改正后的双重约束区域中进行匹配,并对匹配结果进行加权最小二乘拟合定位。实际的宽基线立体影像试验结果证明了算法的有效性,可为后续的三维重建提供较为可靠的密集或准密集匹配点。

尺度不变特征变换;准密集匹配;仿射不变;单应映射

1 前 言

三维重建,即从二维图像恢复三维物体可见表面的几何结构的过程,一直是数字摄影测量与计算机视觉的重要研究内容。其主要涉及影像匹配得到同名像点及在物方空间对表面进行三维重建两大核心技术[1]。目前的三维重建技术已相对较为成熟,因而问题的关键在于如何快速得到稠密或至少是准稠密(quasi-dense)的匹配点。为此,数字摄影测量与计算机视觉领域的广大研究人员对立体影像匹配问题进行了大量的科学研究,出现了许多具有较高参考价值的理论研究成果[1-11]。然而目前大多数性能较优的同名点密集匹配算法多是针对短基线摄影条件的[1-5],即匹配时多直接在影像上取矩形窗口,采用基于区域(area-based)的或基于特征(feature-based)的匹配方法完成相似性判断。而对于存在较大几何变形的宽基线影像而言,此种直接匹配方法的可靠性将大为降低。现有的宽基线立体匹配研究的基本思路是:利用仿射变换近似图像局部区域之间的对应关系并进行仿射变形改正,然后在几何变形改正后的邻域上完成相似性判断并进行迭代匹配传播(match propagation)。此外,在匹配传播前,还需首先获得若干初始稀疏匹配。如:文献[6]选用 Hessian-Affine[7]、文献[8]则综合选用Hessian-Affine及MSER[7]实现初始稀疏种子匹配并基于二阶梯度矩及主方位估计来恢复其对应邻域的仿射关系;而在匹配传播阶段,上述算法均在初始种子匹配估计得到的核线几何约束下来更新新匹配点对应邻域的仿射关系并进行几何变形改正,然后在视差梯度、置信度等约束下,采用基于NCC(normalized cross correlation)测度的区域匹配及全局“最优最先”(best first)的策略进行逐像素(pixel-to-pixel)的匹配传播。所不同的是,文献[6]使用一种代表局部形状的二阶强度矩、而文献[8]则通过邻域3参数仿射参数传递的方式来获得新匹配点对应邻域的仿射关系。文献[9]的方法则通过人工选取特征点对整幅图像进行校正,以简化匹配传播点对应邻域仿射参数的求取,但却使得算法的实用性受到限制。文献[10]和[11]分别研究了基于 Harris和尺度不变特征变换(scale invariant feature transformation, SIFT)算法的宽基线立体影像最小二乘匹配算法。上述算法总体上存在着计算复杂度高且可靠性不足的缺陷。如计算机视觉界的准密集匹配方法多采用仿射不变区域特征的重心作为稀疏匹配点,精度无法保障,而以此估计的核线也是粗略的,对后续匹配传播的约束缺乏精确性。此外,该类方法中基于逐像素的匹配传播策略计算复杂度较高。而基于Harris和SIFT特征点的最小二乘匹配方法涉及较多的平差迭代参数,计算复杂度亦较高且难以获得可靠的密集匹配点。

SIFT算法主要包括尺度空间极值点检测、特征点主方位确定、特征描述符生成及特征匹配四个主要步骤[12]。SIFT特征是图像的局部特征,具有多量性、独特性(distinctiveness)好和信息量丰富的特点,且其对旋转、尺度缩放、亮度变换保持不变性,对视点变化、仿射变换、图像噪声等也保持一定程度的不变性。SIFT算法的上述特点使得其在宽基线立体影像匹配中得到了广泛应用的研究和应用。然而:①SIFT特征描述符不具完全的仿射不变性;②宽基线立体影像特征提取的重复率(repeatability rate)较低。上述两个因素极大地影响了SIFT特征匹配的数量和准确率,难以获得可靠的密集匹配,不利于后续的三维重建。综合考虑上述因素,并充分利用SIFT特征检测结果的多量性特点,提出基于对极几何和单应映射双重约束及SIFT特征的宽基线立体影像多阶段密集匹配算法,并选取实际的宽基线立体影像对算法进行试验。

2 算 法

算法整体流程如图1所示,主要包括如下三个阶段:①基于空间分布和信息熵优选部分较优的SIFT特征点并进行最小二乘初始稀疏匹配及基本矩阵和单应矩阵估计[13-14];②对于其余特征,利用同名核线倾斜角及SIFT特征的尺度信息对匹配窗口进行仿射迭代优化及改正、提取仿射不变SIFT特征描述符,并基于双重约束信息及欧氏距离测度进行匹配;③考虑到宽基线立体影像较低的特征提取重复率,对未能成功匹配的特征点,采用基于邻域参数自适应传播及基于盒滤波(box filter)[15]快速计算的 SSD(sum of squared difference)测度[10]进行双向约束搜索匹配,并对匹配结果进行加权最小二乘曲面拟合定位。算法各阶段的匹配策略和方法详细介绍如下。

2.1 第一阶段匹配

SIFT特征点包含三类信息:位置(x)、所处尺度(σ)和方向(θ)。如图2,十字丝代表特征点所处位置,圆的半径代表其所处尺度,而矩形虚线框代表SIFT特征描述符的提取窗口,箭头代表方位。不失一般性,现假设 m1(xm1,σm1,θm1)和m2(xm2,σm2,θm2)为立体像对 I1、I2中检测到的一对同名SIFT特征点。并设σm1≥σm2,s=(σm1/ σm2),θ=(θm1-θm2)。以同名特征点 m1、m2为坐标原点的两个相关窗口记为W1、W2,大小为(2w+ 1)×(2w+1)。记 m2的邻域窗口坐标 x=[x y]T∈[-w w],x2= [x2y2]T为 x按式(2)进行仿射变换后的坐标。则W1、W2窗口表达为

上式中的A可用式(2)表达。

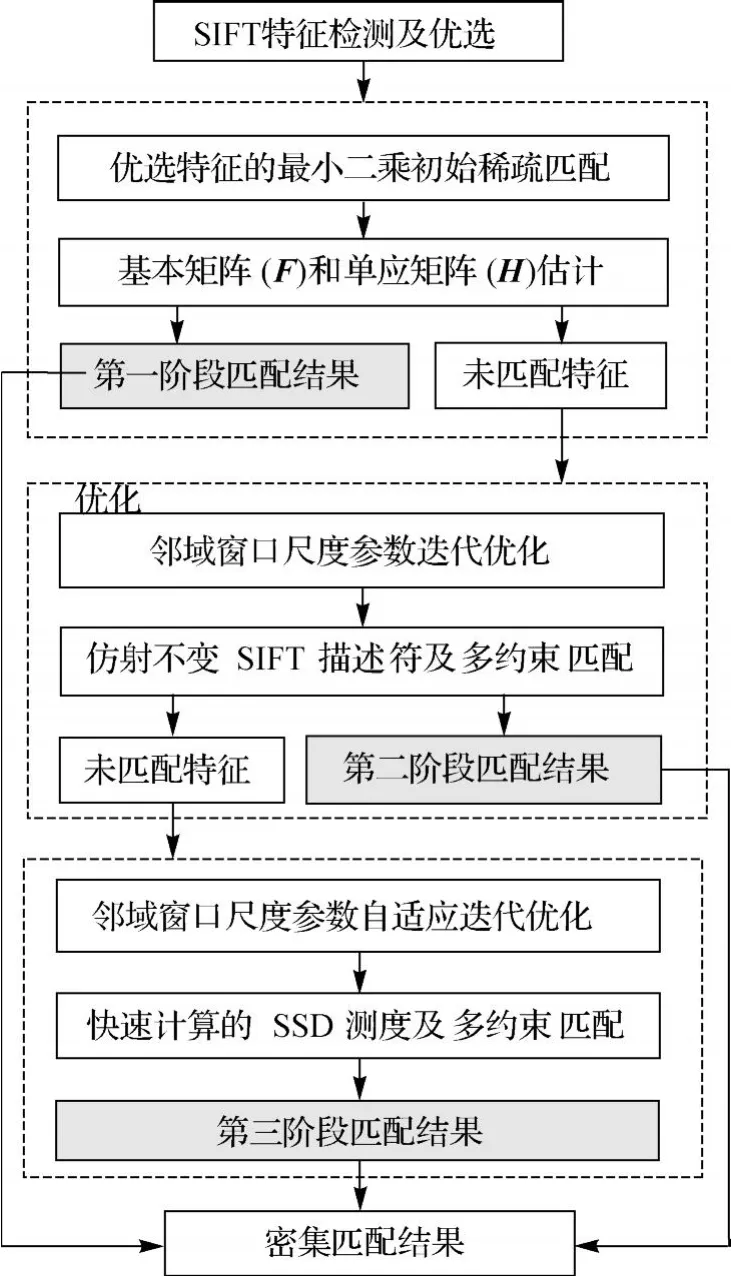
图1 算法流程Fig.1 Flow chart of the proposed algorithm

图2 SIFT特征检测与描述示意图Fig.2 Illustrated figure of SIFT detection and description

式中,sx、sy为x、y两个方向上的缩放因子;δ为特征点相关窗口相对旋转角度。由于 m1和 m2为同名像点,有如下关系式成立

式中,h0、h1为影像窗口之间的线性灰度畸变参数;n1(x2,y2)、n2(x,y)为影像的随机噪声。上式线性化后可得最小二乘匹配的误差方程式,误差方程式及其各项系数以及求解过程详见文献[16]。

最小二乘影像匹配需要良好的待求参数初始值,基于SIFT特征的尺度和方位信息,并考虑到方位确定的误差(由SIFT算法的特征点方向确定的计算过程可知,特征点方向确定本身存在较大的偏差,一般在15°以内),待求参数初始值按下式确定

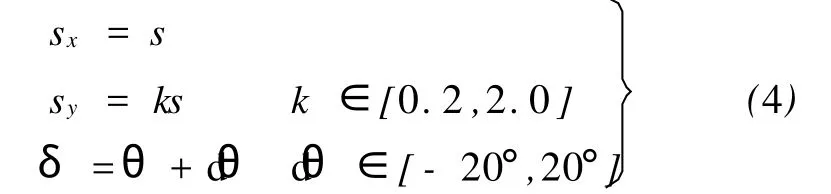
考虑到计算速度及基本矩阵 F和单应矩阵H估计的可靠性,算法通过多层次空间分布约束和尺度空间信息熵度量来优选部分SIFT特征进行最小二乘匹配[11]。最小二乘匹配结束后,利用高精度的稀疏匹配结果采用随机采样一致性算法来计算 F和 H[13]并记录该阶段匹配特征点间的比例因子s和最优的k值kopm,以用于后续两个匹配阶段的尺度参数传递。

2.2 第二阶段匹配

为提高计算速度,第二阶段采用忽略平移向量的4参数仿射变换模型。

如图3,m1和m2的同名核线方程分别记为

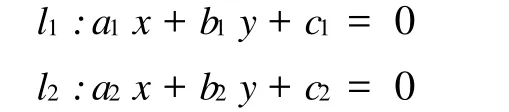
易得同名核线的倾斜角分别为

图3 匹配窗口仿射变形改正Fig.3 Affine rectified for matching window

图3中以m2为中心的矩形窗口W2首先旋转α-β角度得到窗口区域U2,则此时以m1为中心的邻域窗口U1与U2间仅存尺度变换关系。进一步考虑尺度变形因素,则图3和式(1)中的A表达为

第一阶段匹配已获得了较为精确的核线几何关系,因此,在第二阶段匹配时将核线的倾斜角视作定值。由此,式(4)仅需尺度变形因子sx、sy需要确定。在变形改正后的窗口中提取SIFT特征描述符并基于欧氏距离计算相似性测度,选择相似性测度最小者对应的k值即可按式(4)和式(5)确定最优仿射参数并同时确定匹配点。记录该阶段匹配特征点间的比例因子 s和最优的 k值kopm,以用于第三阶段匹配时的尺度参数传递。

2.3 第三阶段匹配

第二阶段未能正确匹配的SIFT特征,多数是由于宽基线立体影像较低的特征提取重复率引起的。有鉴于此,算法对第二阶段未能正确匹配的特征点进行双向约束匹配,并采用如下策略和方法:

(1)邻域窗口尺度参数自适应迭代优化。双向匹配是以立体像对中其中一张影像中检测的特征点为基础,而在另一张影像中基于多信息约束进行穷举搜索匹配,因而式(4)中的s无法根据SIFT特征的尺度信息直接确定。考虑到上述两个阶段的匹配已经获得了一定数量的匹配点,因而,尺度参数可根据已匹配点间的尺度信息确定。采用如下自适应策略:首先找到与待匹配点距离最近的已匹配点,设最近距离为D,给定阈值DT,如D大于DT,则需首先按式(6)定义的SSD匹配测度优化式(4)中的尺度比例因子s;继而再优化sy;如D小于DT,则直接按式(4)优化sy,且在优化sy时,仅需在已匹配特征点的 kopm的较小邻域内进行。上述自适应策略保证了邻域尺度参数传递的速度和准确性。

(2)基于盒滤波技术快速计算的SSD匹配。第三阶段匹配需在约束的邻域范围内进行穷举搜索,匹配运算较为耗时。为此,算法采用如下策略:现假设右影像 I2中的特征点 m2在左影像 I1中的核线为l1,双重约束搜索区域为图4中右图阴影部分(记为Ω1),首先对Ω1的中心m按上述第(1)步的方法进行仿射参数优化,根据优化结果对Ω1进行几何变形改正,在改正后的邻域Ω2中采用基于盒滤波快速计算的SSD匹配测度进行相似性搜索。采用盒滤波技术在计算窗口匹配代价时充分利用了前一个像素的累积结果,消除了冗余计算,其计算一个后续窗口的差异和,只需计算4个点。

图4 双重约束区域仿射变形改正Fig.4 Affine rectified for dual constraint region

如仅基于核线几何约束,则可沿核线两侧邻域进行分段校正,再采用快速的SSD匹配算法。

(3)匹配点加权拟合定位。在匹配点的3×3邻域窗口内,依匹配测度进行加权多项式拟合,以其极值点的位置作为最佳匹配点。考虑如下多项式

式中,f(x,y)=1/CSSD(x,y)。为突出窗口中心像素的重要性,对窗口各像素采用高斯距离加权,即

采用最小二乘法拟合二次多项式后,极大值点的位置(xmax,ymax)可按下式求出

3 试验与分析

3.1 试验数据及评价指标

选取实际的具有不同纹理类型的两宽基线立体影像序列,分别是 Graffiti Sequences和 Wall Sequences(http:∥www.robots.ox.ac.uk/～vgg/data/data-aff.html)的前4幅影像(分别记作img1、img2、img3及img4)。Graffiti和Wall序列立体影像间存在不同程度的仿射变形。各序列影像之间的单应矩阵 H0已知。利用已知的单应矩阵按式(10)将待匹配影像投影到参考影像,以投影误差作为同名点匹配定位精度的评价指标,并对其设一阈值ε0,如投影误差小于ε0,则认为该对点是匹配的。以下的试验中取ε0=3.0像素。

3.2 试验结果与分析

在 Microsoft XP操作系统下基于 Visual C++6.0及OpenCV(开放计算机视觉函数库)集成开发环境编写了算法试验程序。相关试验结果如下:①图5和图6分别给出了两立体影像序列中各像对各阶段基于双重几何约束时及仅基于核线几何约束时的正确匹配对数(第一阶段未施加约束);②表1列出了两影像序列中视点变化为40°的img1-img4立体像对各阶段的正确匹配/总匹配数量(n1/n2)和匹配正确率(p%);③表2给出了两立体影像序列中各像对LSM-SIFT算法与本文算法的匹配定位误差(e= [ε ε]/n ,ε按式(10)计算,n为总匹配点数量)对比;④图7和图8分别给出了两影像序列中img1-img4立体像对的最终匹配结果图及文献[11]LSM-SIFT算法的匹配结果,图7(a)和图8(a)的局部放大图中(相对图像原始分辨率放大2倍)红色标记点为本文算法第一阶段的匹配点,白色为第二阶段的匹配点,而绿色和黄色点分别为第三阶段中从左至右和从右至左的匹配点。经检验,图7(a)局部放大图中除蓝色圆标出的点外,其余的白色点和红色点是LSM-SIFT算法的匹配点;而图8(a)局部放大图中的白色点和红色点均是LSM-SIFT算法的匹配点。

图5 两立体影像序列中各像对各阶段基于双重几何约束时的正确匹配点数量Fig.5 Correct matching number of each stage for every pairs from two stereo image sequences with dual geometric constraints

图6 两立体影像序列中各像对各阶段仅基于核线几何约束时的正确匹配点数量Fig.6 Correct matching number of each stage for every pairs from two stereo image sequences with epipolar constraint only

表1 两立体影像序列中img1-img4像对各阶段的匹配结果Tab.1 Matching results of each stage for img1-img4 pairs from two stereo image sequences

表2 两序列立体影像各像对不同算法的匹配定位误差对比Tab.2 Comparison of matching errors using different algorithms for each pairs from two stereo image sequences 像素

图7 Graffiti Sequences(img1-img4)的匹配结果Fig.7 Matching results for Graffiti Sequences(img1-img4)

图8 Wall Sequences(img1-img4)的匹配结果Fig.8 Matching results for Wall Sequences(img1-img4)

综合上述试验结果,分析如下:

(1)充分顾及宽基线立体影像特征提取的重复率,通过第三阶段的双向匹配策略可显著提高匹配点的数量。如对存在较大仿射变形的Graffiti和Wall Sequences中的img1-img4立体像对,通过第三阶段的匹配,使匹配点的数量分别增加了1 452和2 816个(表 1及图 5)。又如,图 5(b)Wall Sequences中的立体像对img1-img2(视点变化为20°),左右影像初始检测的特征点数分别为5 361个和6 419个,但最终正确匹配点的数量为8 446个。由此可见,本文算法使得宽基线立体影像的匹配性能不再受特征提取重复率的限制,使SIFT的冗余特征变得不再“冗余”,并可利用其获得较好的密集或准密集匹配结果。

(2)文献[11]业已证明,LSM-SIFT算法在正确匹配点的数量和匹配定位精度方面优于现有的基于 SIFT的特征匹配方法。但图7(b)和图8(b)表明,该方法难以获得密集匹配,尤其是对具有大量结构和纹理信息的 Graffiti立体影像对,主要原因在于LSM-SIFT算法对宽基线立体影像特征点较大的提取和定位误差较为敏感。如图7(a)局部放大图中蓝色圆标出的一对点,其定位误差为2.43像素,则LSM-SIFT算法未能取得成功匹配。本文算法除第一阶段外,第二阶段采用了对特征点定位误差具有一定抗差性的SIFT特征匹配方法,第三阶段匹配则充分考虑了宽基线立体影像较低的特征提取重复率的影响而采用双向双重约束搜索策略,从而显著提高了匹配点的数量。此外,虽然本文方法的匹配定位精度同LSM-SIFT算法相比有较大差距(表2),但对于匹配难度较大的宽基线立体影像及大多数3维重建任务而言,匹配点的数量要比匹配精度重要得多。另一方面,基于NCC的LSM-SIFT算法迭代运算涉及的平差参数较多,而且,由于宽基线立体影像变形较大,平差参数的初始值难以精确给定,导致迭代收敛时间较慢。而本文方法仅仅优选部分特征点进行最小二乘匹配(第一阶段),而在第二、第三阶段分别采用运算速度较快的SIFT特征描述符和快速的SSD算法,试验结果表明本文方法的匹配时间要低于LSM-SIFT算法。如图7(a)和图7(b)的匹配耗时分别为118.7 s和147.6 s。

(3)对比图5和图6可知,如仅基于核线几何约束,匹配点的数量会有较大幅度的下降。如Graffiti和 Wall Sequences中视点变化为40°的img1-img4立体像对基于双重约束和仅基于核线约束的总匹配点数量分别为(1 762,1 087)和(3 515,2 235)。但从匹配点的绝对数量来看,仍可获得密集至少是准密集的匹配点(限于篇幅,匹配结果图像不再给出)。

4 结 论

本文充分利用SIFT特征检测结果的密集性特点,并同时考虑到宽基线立体影像的仿射几何变形、匹配约束条件及最终匹配点的数量要求,有针对性地将密集匹配算法划分为三个阶段,并对三个不同的匹配阶段采用不同的匹配策略和方法,以提高匹配的准确性和计算速度。试验结果表明本文算法可显著提高匹配点的数量和匹配准确率,获得较为可靠的密集匹配点,有利于后续的摄影测量三维重建。需要指出的是,全局单应约束仅适合平面或近平面场景。因此下一步的研究重点是借助仿射不变区域特征(如Harris-Affine及MSER等)对非平面场景进行单应面估计和划分,在多个单应面内采用本文算法进行匹配,而对于非单应面内的点,则采用核线几何约束及拓扑几何关系进行匹配,通过上述策略扩展本文算法的适用范围。

[1] YUAN Xiuxiao,MING Yang.A Novel Method of Multiimage Matching Using Image and Space Synthesis Information[J].Acta Geodaetica et Cartographica Sinica,2009,38 (3):216-222.(袁修孝,明洋.一种综合利用像方和物方信息的多影像匹配方法[J].测绘学报,2009,38(3):216-222.)

[2] ZHU Qing,WU Bo,ZHAO Jie.Propagation Strategies for Stereo Image Matching Based on the Dynamic Triangle Constraint[J]. ISPRS Journal ofPhotogrammetry & Remote Sensing,2007,62(4):295-308.

[3] HUA Shungang,ZENG Lingyi.Dense Matching Algorithm Based on Corner Detection[J].Computer Engineering and Design,2007,28(5):1092-1095.(华顺刚,曾令宜.一种基于角点检测的图像密集匹配算法[J].计算机工程与设计,2007,28(5):1092-1095.)

[4] TANG Liang,WU Chengke,CHEN Zezhi.Image Dense MatchingBasedon Region Growth with Adaptive Window[J]. Pattern Recognition Letters,2002,23(10):1169-1178.

[5] L HUILLIER M,QUAN L.A Quasi-dense Approach to Surface Reconstruction from Uncalibrated Images[J]. IEEE Transactions on Pattern Analysisand Machine Intelligence,2005,27(3):418-433.

[6] KANNALA J,BRANDT S.Quasi-dense Wide Baseline Matching Using Match Propagation[C]∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Minneapolis:IEEE,2007.

[7] MIKOLAJCZYK K,TU YTELAARS T,SCHMID C.A Comparison of Affine Region Detectors[J].International Journal of Computer Vision,2005,60(1):163-186.

[8] XU Zhenhui,ZHANG Feng,SUN Fengmei,et al.Quasidense Matching by Neighborhood Transfer for Fish-eye Images[J].Acta Automatica Sinica,2009,35(9):1159-1167. (许振辉,张峰,孙凤梅,等.基于邻域传递的鱼眼图像的准稠密匹配[J].自动化学报,2009,35(9):1159-1167.)

[9] MEGYESI Z,KOS G,CHETVERIKOV D.Surface Normal Aided Dense Reconstruction from Images[C]∥Proceedings of Computer Vision Winter Workshop.Telc: [s.n.],2006.

[10] DENG Baosong,SONG Hanchen,YANG Bing.Feature Point Matching Based on Affine Iterative Model[J]. Journal of Image and Graphic,2007,12(4):678-683.(邓宝松,宋汉辰,杨冰.基于仿射迭代模型的特征点匹配算法[J].中国图象图形学报,2007,12(4):678-683.)

[11] YAN G Huachao,ZHAN G Shubi,ZHAN G Qiuzhao. LeastSquaresMatching Methods forWide Base-line Stereo Images Based on SIFT Features[J].Acta Geodaetica et Cartographica Sinica,2010,39(2):187-194.(杨化超,张书毕,张秋昭.基于SIFT的宽基线立体影像最小二乘匹配方法[J].测绘学报,2010,39(2):187-194.)

[12] LOWE D.Distinctive Image Features from Scale-invariant Keypoints[J].International Journal of Computer Vision, 2004,60(2):91-110.

[13] LIANG Dong,TONG Qiang,QU Lei,et al.Algorithm for Images Matching Based on Epipolar and Homography Constraints[J].Journal of System Simulation,2006,18(1): 44-46.(梁栋,童强,屈磊,等.一种基于极几何和单应约束的图像匹配算法[J].系统仿真学报,2006,18(1): 44-46.)

[14] HARTLEY R I,ZISSERMAN A.Multiple View Geometry in Computer Vision[M].Cambridge:Cambridge University Press,2003.

[15] WANG Xin,MA Yan,YANG Jian,et al.Implementation and Improvement ofArea-based Stereo Matching Algorithm[J].Optics and Precision Engineering,2008, 16(10):2002-2008.(王昕,马岩,杨剑,等.区域立体匹配算法的实现与改进[J].光学精密工程,2008,16(10): 2002-2008.)

[16] ZHANGJianqing,PAN Li,WANG Shugen.The Photogrammetry[M].Wuhan:Wuhan University Press,2003. (张剑清,潘励,王树根.摄影测量学[M].武汉:武汉大学出版社,2003.)

Dense Matching for Wide Base-line Stereo Images Based on SIFT

Y ANG Huachao1,2,Y AO Guobiao2,WANG Yongbo1,2
1.Key Laboratory for Land Environment&Disaster Monitoring of SBSM,Xuzhou 221116,China;2.School of Environmental& Spatial Informatics,China University of Mining&Technology,Xuzhou 221116,China

A novel multi-stage quasi-dense matching algorithm for wide base-line stereo images is introduced based on SIFT and dual constraints of epipolar geometry and homographic mapping.The proposed algorithm includes following three stages:①The optimal SIFTfeatures with good spatial distribution and large information content are first selected,and matched by using the least squares matching method,then the fundamental and homographic matrix can be estimated by using these initial sparse correspondences with higher precision;②For the other SIFT features,the affine transformation parameters between matching windows are iteratively optimized by using the slope angle of correspondent epipolar lines and scale information of SIFT features,and affine invariant feature descriptors are extracted from the corrected matching windows,then correspondences can be determined by Euclid distance and dual constraint information;③Considering the lower repeatability rate of feature detection for wide base-line stereo images,for the unmatched points extracted from left and right images of stereo pairs,matching can be carried out by adopting two-way search strategy from left to right image or from right to left image based on the rapid SSD similarity cost function and affine rectified dual constraints region,and the least squares curve surface fitting weighted by Gaussian-distance algorithm is adopted to improve the precision of matching results. Test results using practical wide base-line image pairs indicate the proposed algorithm is effective and can provide reliable dense or quasi-dense matching points for subsequent 3D reconstruction.

scale invariant feature transformation;quasi-dense matching;affine invariant;homographic mapping

Y ANG Huachao(1977—),male,Post PhD, associate professor,majors in digital photogrammetry and remote sensing images processing.

1001-1595(2011)05-0537-07

P237

A

国家自然科学基金(41001312;41001297;61072094)

(责任编辑:雷秀丽)

2010-10-11

2011-01-17

杨化超(1977—),男,博士后,副教授,主要研究方向为数字摄影测量、遥感图像处理。

E-mail:yanghc3344@yahoo.com.cn