基于改进多目标微粒群算法的模具多项目反应调度

张沙清 陈新度 陈庆新 陈 新

广东工业大学，广州，510006

基于改进多目标微粒群算法的模具多项目反应调度

张沙清 陈新度 陈庆新 陈 新

广东工业大学，广州，510006

针对模具多项目执行过程中由于可再生资源发生故障、任务拖期以及随机插入新项目而导致的调度计划变更问题，提出了一种反应调度算法。利用生灭过程理论对可再生资源的不确定性进行分析，并采用基于优先规则的拓扑排序方法构建初始调度计划，建立了以调度计划变更产生的附加费用最小以及项目加权工期之和最小为目标的多目标反应调度模型，并提出一种改进的多目标微粒群算法进行模型求解。最后，通过仿真计算分析了反应调度算法的可行性与有效性。

任务拖期；资源不确定；反应调度；多目标微粒群算法

0 引言

在模具项目执行过程中经常会出现各种突发事件，如资源发生故障、任务拖期、随机插入新项目、工程与生产变更等，结果导致开始制订的项目计划被破坏。只有采取科学的多项目动态调度与协同监控手段，才能有效地应对突发事件，确保项目顺利进行。目前，专门研究风险性和不确定环境下项目调度理论与方法的文献较少。对现有文献进行初步归类，可以大致分为两大类：第一类将项目网络图的结构假设为确定的，而将项目中的其他参数，如任务工期等作为不确定性变量，对项目调度方案的制订展开研究，文献［1］全面地综述了这类研究工作，认为主要存在四种不同的调度方法，即反应性调度、随机性调度、模糊调度和前摄鲁棒性调度；第二类将项目网络图的结构假设为随机的，研究项目调度计划与控制方法，文献［2－3］介绍了这类研究工作。

就模具项目调度而言，文献［4］对确定条件下的多个模具项目的工期费用规划作了初步研究，文献［5－6］在单个模具项目的工期与费用的不确定性规划方面作了大量的研究，文献［7］研究了具有工件约束的模具零件制造的动态调度问题，文献［8－9］考虑了任务工时、费用、质量、是否返修等不确定因素，基于Markov理论，研究了基于启发式策略仿真和Q学习算法的多模具制造过程的随机调度问题，但针对不确定环境下多个模具项目的分析、设计、制造过程的动态调度研究，国内外文献并不多见。

本文从多目标优化的角度出发，研究在可再生资源（以下简称资源）发生故障、任务拖期、随机插入新项目等多种不确定因素影响下的模具多项目反应调度算法。

1 问题描述

一个典型完整的模具项目的网络拓扑结构如图1所示，其中每个节点（圆圈表示）表示一个任务，共有16个任务，各任务名称及其对资源的需求如表1所示。由于模具项目的分析、设计与制造的工艺流程大致相同，因此它们的网络拓扑结构也大体相同，因此可以把多个模具的网络结构图采用并行连接的方法合并为一个网络图G＝（N，A），首尾加两个虚拟节点，并对各节点重新编号，其中，N为网络中的节点（包括虚拟的开始节点和结束节点），A为任务之间的紧前约束关系集合，即若任务i为任务j的前驱，则弧（i，j）∈A。图2为三个模具项目的网络结构图，其中0、49号节点分别表示虚拟的开始任务和结束任务，工期为0，也不需要任何资源。

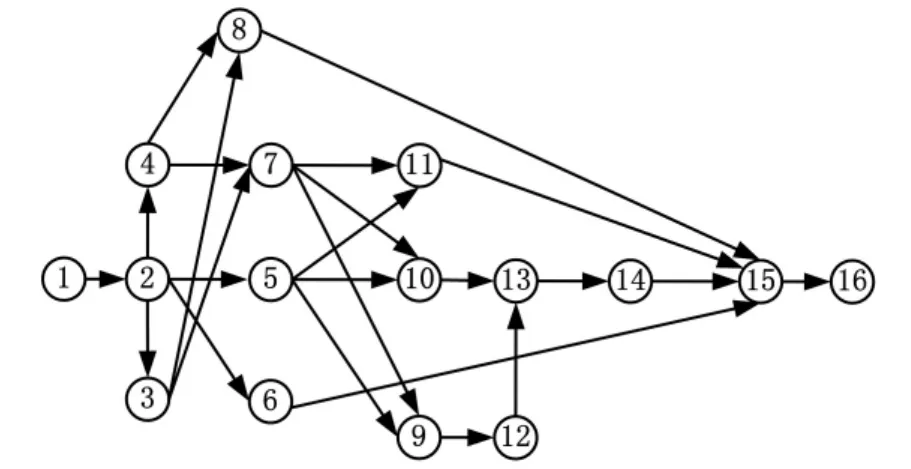
图1 模具项目网络拓扑结构图

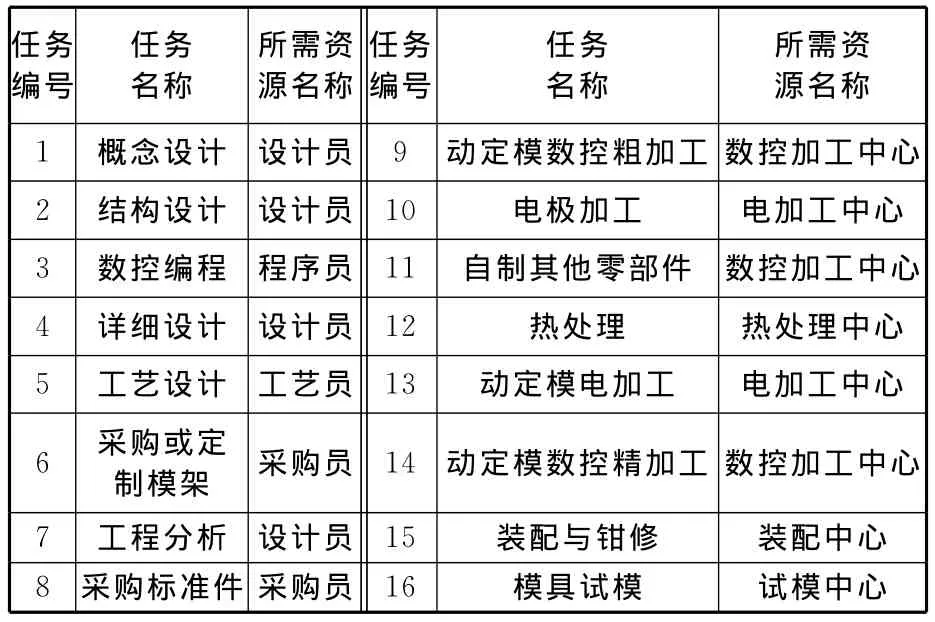
表1 任务资源需求表

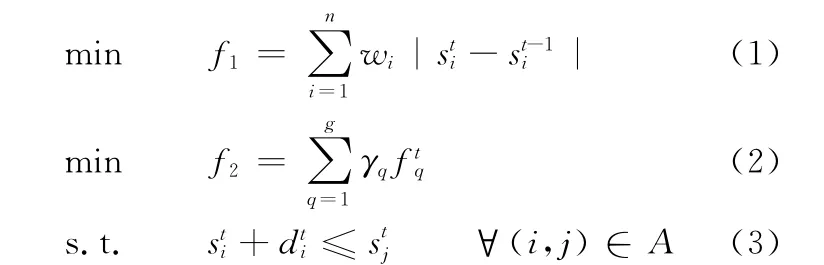
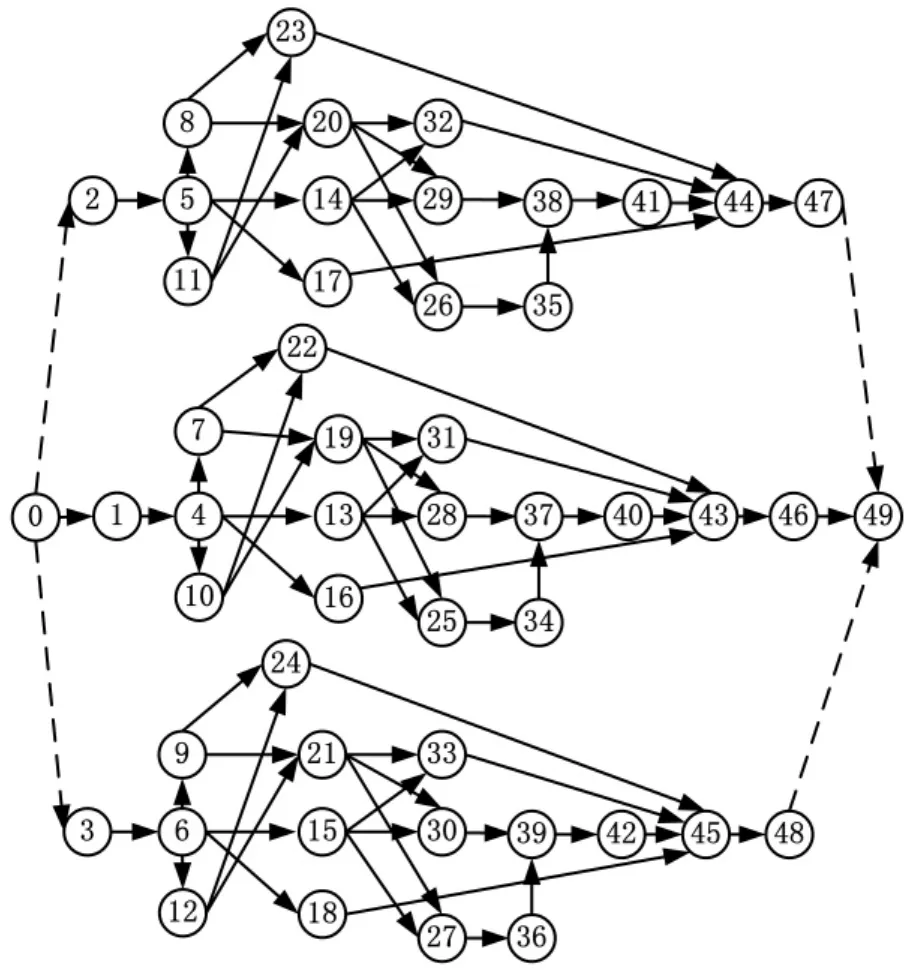
图2 三个模具项目的网络拓扑结构图

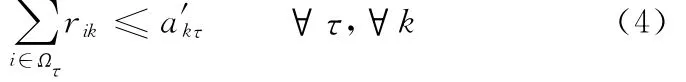
模具生产过程中，首先需要制订一个初始调度计划，然后执行该初始计划。在项目执行过程中，当可用资源数量不足、任务拖期或随机插入新项目导致正在执行的调度计划St－1无法继续执行时，则进行反应调度，产生一个新的调度计划St。本文提出的反应调度的优化目标为：①St与St－1的偏差最小，通常用因反应调度产生的计划变更而带来的附加费用来衡量这种偏差［10-11］，附加费用越小则偏差越小；②St的项目加权工期之和最小，从而减少由于项目拖期而造成的高额罚款。上述优化目标可用如下模型进行描述：式中，n 为G 中非虚 拟任务的 个 数、分 别为St、St－1中任务i的计划开始时间为St中任务i的工期；wi为任务i的权重，表示反应调度后任务i开始时间每变更一个时间单位所产生的附加费用的相对大小，假设其大小符合一个离散的三角分布，即wi＝z的概率P由下式确定［12］：P（wi＝z）＝（21－2z）%，z∈ ｛1，2，…，10｝；g 为项目个数（包括可能随机插入的新项目）为St中项目q的计划完成时间；γq为项目q的重要性权重；rik为任务i每个时段所需的资源k的数量；Ωτ为时间段τ正在执行的任务的集合；a′kτ为τ时段资源k的可用数量。

式（1）、式（2）表示多目标优化模型的两个优化目标，式（3）表示任务之间的紧前约束条件（即任意一个任务必须在其所有前驱任务完成之后才可以开始），式（4）表示资源约束条件（即任意一个时段正在执行的任务所需要的各类资源数量不能超过该时段各类资源的可用数量）。

对于上述多目标优化模型，有以下定义：

2 初始调度计划的构建

2.1 基于生灭过程的资源不确定性分析

通常，机器发生故障的时间间隔与机器的修复时间均服从一定参数的指数分布。如果工作人员（如前述的设计员、程序员、工艺员、采购员）因各种原因而发生缺勤的时间间隔，以及人员缺勤的时间也服从指数分布，则可用生灭过程来分析资源的不确定性。为方便起见，将机器故障与人员缺勤统一描述为资源故障，而将机器修复与人员复工统一描述为资源修复。

设项目执行共需要K类资源，t＝0时资源k（k∈K）的总量为ak，资源k的平均故障时间间隔为TF，k，平均修复时间为TR，k。任意时段t的系统状态jk表示故障资源k的个数为jk（为了描述方便，暂时省去下标k）。若生灭过程在时段t处于状态j，则该过程的状态转变服从如下两个定理。

定理1［15］在时段t和t＋Δt之间出现“生”的概率为λjΔt＋ο（Δt），“生”使系统状态增加1，成为j＋1，变量λj称为状态j下的出生率；在时段t和t＋Δt之间出现“灭”的概率为μjΔt＋ο（Δt），“灭”使系统状态减少1，成为j－1，变量μj称为状态j下的灭亡率，μ0＝0必须成立，否则可能出现负状态。

定理2［15］“生”和“灭”彼此独立。

显然，本文中的“生”指资源发生故障，“灭”指资源被修复。因此，有λj＝ （a－j）／TF，μj＝j／TR。状态j的稳态概率πj可以通过求解如下的流量平衡方程而得到［15］：

2.2 基于拓扑排序的初始调度计划构建

初始调度计划的构建为典型的资源受限项目调度问题（resource constrained project scheduling problem，RCPSP），目前的解法主要有精确算法和启发式算法两大类。对于规模较大的RCPSP问题主要采用后者进行求解。本文中令资源k单位时段的可用数量为E（ak），采用一种基于优先规则的拓扑排序法来产生一个项目加权工期之和最小的初始调度计划［16］。

3 基于改进多目标微粒群算法的反应调度

3.1 反应调度算法描述

设S0表示时间t＝0时执行的调度计划，则本文提出的反应调度算法流程如下：①初始化，t＝0，St＝S0；②若时间t所有任务全部完成，则调度结束，否则转向步骤③；③若时间t出现资源不足、任务拖期或插入新项目的情况，则转向步骤④，否则St＝St－1，转向步骤⑤；④将当前正在执行的调度计划St－1中计划完成时间不小于t的任务及其时序关系组成新调度的项目网络图，并采用改进的多目标微粒群算法求出新的调度计划St；⑤开始执行St中所有开始时间为t的任务；⑥t←t＋1，返回步骤 ②。

上述算法步骤④中，对于在t时段正在执行的任务，进行反应调度时通常有两种处理模式，即所谓的Preempt－repeat模式和Preempt－resume模式。前者指的是在t之前的工作完全损失，反应调度时该任务需要从头开始执行，而后者指的是在t之前的工作不会损失，反应调度时该任务从中断处继续开始执行。本文采用Preempt－repeat模式，同时假设在没有出现资源不足、任务拖期或插入新项目的情况下，正在执行的任务所使用的资源不能被强占，即任务不能被中断（简称为不可强占资源）。

3.2 改进的多目标微粒群算法

文献［17］提出利用微粒群优化算法解决多目标优化问题，在理论研究和实际应用中都取得了大量的成果。多目标优化的多重任务要求整个群体既要向Pareto最优前端逼近，又要能维持群体的多样性与均匀性，因此在更新微粒位置与速度时，往往面临着一定的矛盾。本文借鉴文献［18］的最优解评估选取方法，将孤立点搜索策略与精英归档策略相结合，提出采用一种改进的多目标微粒群算法（improved multi－objective particle swarm optimization，IMOPSO）来求解反应调度时的新计划。算法流程描述如下：

（1）初始化，设定算法的各参数（种群规模为M，最大迭代次数为Imax，惯性权重为ω，学习因子分别为c1、c2、c3，精英集的容量大小为Selite）。随机产生每个微粒的位置向量X（i）和速度向量V（i）（i＝ 1，2，…，M），X（i）为对应任务的优先权，为［0，1］之间的随机数，微粒速度为［－0.9，0.9］之间的随机数。分别随机产生每个微粒i在目标函数f1、f2下的最优位置向量Pbest1（i）、Pbest2（i），以及全局最优位置向量Gbest1、Gbest2，置当前迭代次数m＝1。

（2）对每个微粒i，利用修改后的串行调度生成方案［16］产生一个调度计划，分别用目标函数f1、f2计 算 调 度 计 划 的 适 应 值 f1（X（i））和f2（X（i））。

（3）分别求得每个微粒i在目标函数f1、f2下的最优位置向量，即

（6）计算每个微粒的稀疏度，并得到稀疏度最大的微粒，其位置向量记为X（l）。

（7）更新每个微粒的速度向量和位置向量：

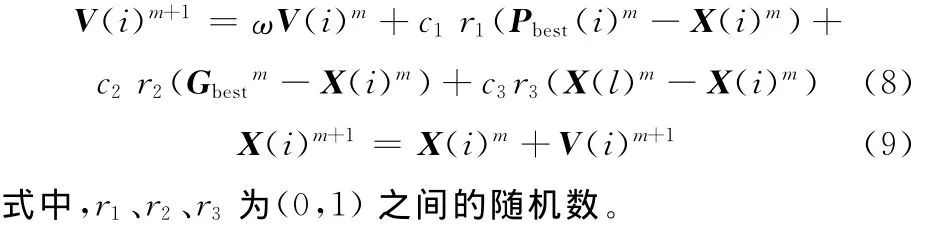
（8）将当前种群中的非劣解加入精英集，并更新精英集（更新算法见3.3节）。

（9）m ←m＋1，若m≤Imax，则返回步骤（2）；否则，转向步骤（10）。

（10）在精英集中选择一个最优折中解（见3.4节），算法结束。

算法步骤（6）中的稀疏度表示种群中个体周围的稀疏程度，它等价于在个体周围包含个体本身但是不包含其他个体的最大的长方形。“稀疏度”越大的个体与其周围邻近的个体的平均距离越大，因而该个体周围显得越稀疏，“稀疏度”最大的个体称为孤立点。在解空间进行搜索时，使微粒朝着群体分布最为稀疏的区域飞行，有利于提高解的分布均匀性。分别将微粒按照目标函数f1、f2排序，则微粒i的“稀疏度”可按下式计算［19］：

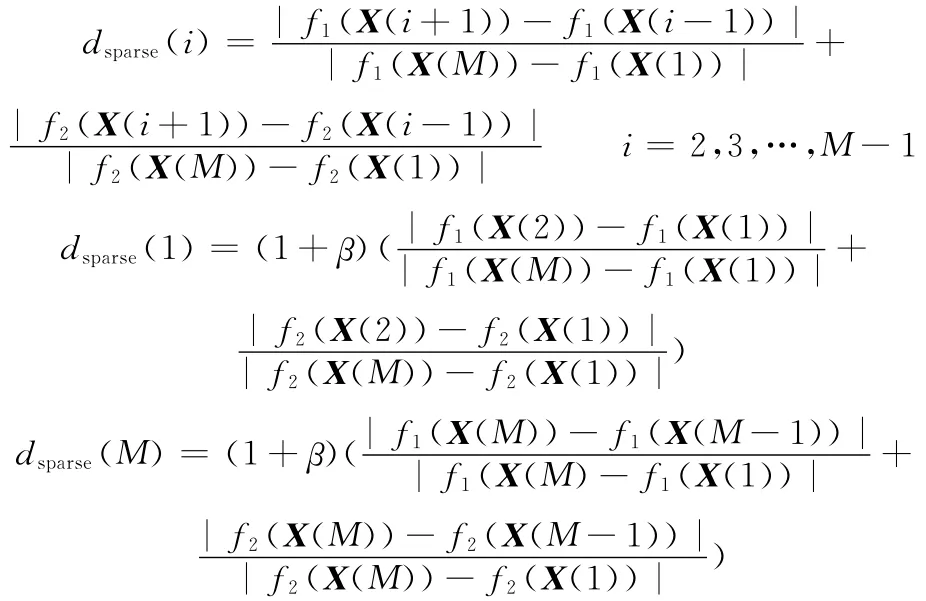
式中，β为（0，1）之间的随机数。

3.3 精英集更新算法

（3）求RN数组中值为1与RE数组中值为1的元素所对应的非劣解的并集。

简单的聚类方法（如K均值聚类）一般需要事先给定聚类的数目，具有较强的主观性，而且对于高维数据（通常认为超过16维即为高维）的聚类效果较差；另外，算法实现过程中往往需要对数据集进行反复聚类，计算效率较低。本文采用一种高性能的层次聚类算法（clusters optimization on preprocessing stage，COPS）对微粒位置向量进行聚类分析。COPS的原理与主要过程是［20］：①将每个数据点看作为一个单独的簇；②自底向上层次式地构造出数据集所有合理的划分组合，进而生成一条关于不同划分的聚类质量曲线；③抽取出对应曲线极小值点的划分来计算数据集的最佳聚类数目；④根据最佳聚类数目确定每个类中的样本个数及其中心。若n′、d分别表示数据集的数据个数与维度，则COPS的时间复杂度仅为O（dn′log2n′），计算效率较高。

3.4 选择最优折中解

由于多目标优化算法得到的解是一组Pareto解集，故项目管理者需要从Pareto解集中选择一个解作为反应调度的结果。本文应用模糊隶属度函数来分别表示每个Pareto解中各个目标函数对应的满意度［21］。设分别表示Pareto解集中目标函数i的最大值与最小值表示Pareto解集中第k个解的目标函数i的值，则Pareto解集中第k个解的目标函数i对应的满意度定义如下：

4 仿真实验

4.1 算例介绍与算法参数设置

某模具厂同时开始三个模具项目，其网络拓扑结构如图2所示，其中编号为46、47、48的任务所在的项目分别为项目1、2、3，其项目重要性权重γ1、γ2、γ3分别为0.35、0.37、0.28。项目所需的各类资源的初始总量、平均故障时间间隔TF、平均修复时间TR如表3所示，项目各任务的权重如表4所示，任务估算工期与资源需求如表5所示。

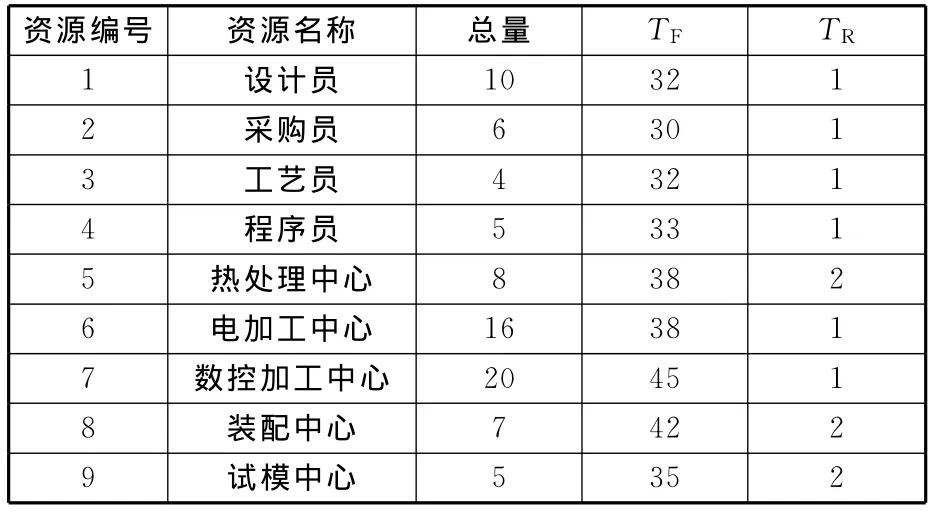
表3 资源名称及其相关数据

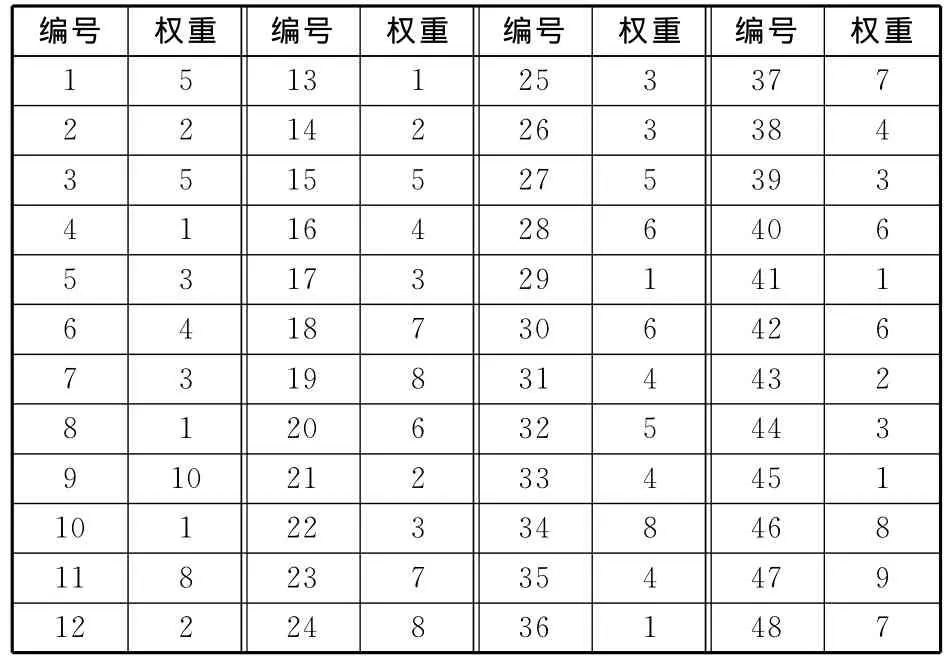
表4 任务编号与其权重

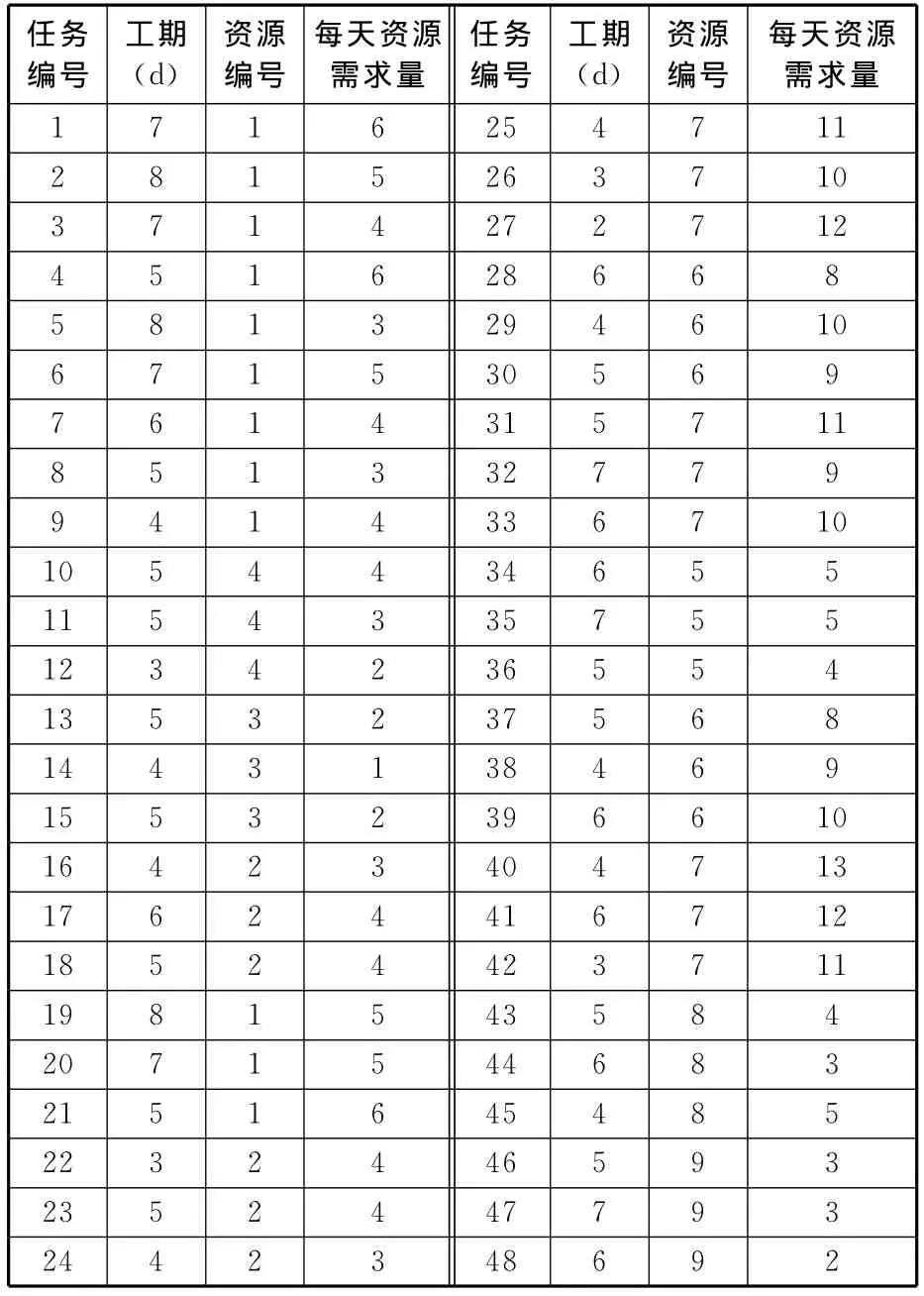
表5 任务估算工期与资源需求

设有一个新项目在第10～15天、第16～25天、第26～35、第36～45天插入的概率分别为10%、20%、40%、30%，其重要性权重为1。新插入项目的各任务的估算工期、资源需求以及任务权重如表6所示。

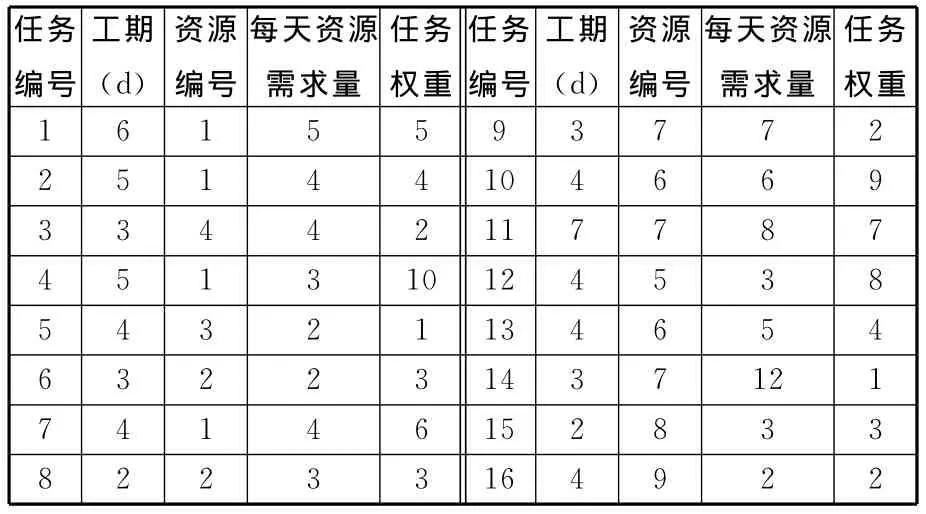
表6 新插入项目各任务估算工期、资源需求与权重

设各任务（包括新插入项目的任务）发生拖期的概率为15%，任务拖期的天数为其估算工期的20%～40%。

微粒群种群规模M＝50，最大迭代次数Imax＝60，精英集容量大小Selite＝120，学习因子c1＝c2＝2，c3＝0.5，惯性权重ω＝exp（－15×（Ic／Imax）10）（Ic为当前迭代次数）。

采用MATLAB7编写应用程序，在配置为Intel（R）Xeon（R）CPU E5335＠2.00GHz 3GB内存的服务器上进行仿真实验。

4.2 仿真结果分析

通常情况下，主要是从解的质量方面评价多目标进化算法的优劣。Zitzler等［22］提出了一系列非劣解的评价指标，然而这些评价指标都是在真实Pareto最优解已知的情况下建立的，称之为理论型评价指标。但是，实际问题的真实Pareto最优解集往往并不知道，理论型评价指标存在一定的局限性。因此，本文用算法实际求得的非劣解集合（近似Pareto最优解集）替代真实的Pareto最优解集，主要采用如下两种应用型评价指标来进行算法优劣的比较：

（1）修正距离Dm［23］。该指标反映算法所得非劣解逼近近似Pareto最优解的程度，定义为

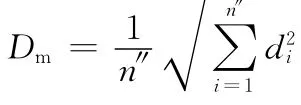
其中，n″为算法求得的非劣解的个数，di为第i个非劣解到近似Pareto最优前端的最小距离。Dm越小，则算法所得非劣解越靠近近似Pareto最优前端，反之亦然。若Dm＝0，则说明非劣解完全落在近似Pareto最优前端。

求得初始调度计划后，对项目执行过程进行了100次随机仿真（从开始执行初始调度计划到各项目全部完成称为一次仿真）。每次仿真过程中，由于资源故障、任务拖期或插入新项目的影响，将出现若干次反应调度。分别采用本文提出的IMOPSO算法和文献［18］、文献［24］中的算法（种群规模、最大迭代次数、学习因子、惯性权重的设置同IMOPSO）进行反应调度，则100次仿真共进行反应调度的次数分别为1659、1684、1662，多次反应调度的Dm平均值平均值如表7所示。

表7 算法性能比较

由表7可知，本文提出的IMOPSO算法性能优于文献［18］和文献［24］中的算法。另外，由于IMOPSO算法和文献［24］中的算法均采用了精英归档策略，所以两种算法所得解全部都是非劣解，而文献［18］算法未采用精英归档策略，结果平均只有74.6%的解为非劣解。

从计算时间上看，IMOPSO算法耗时最长，文献［18］算法次之，文献［24］算法耗时最短，三者的平均反应调度时间依次约为261s、108s、52s。这主要是因为IMOPSO算法的精英归档策略中的聚类算法增加了计算复杂度，而文献［24］中的算法执行流程相对简单，所以耗时最短。

5 结束语

本文分析了资源不确定、任务拖期以及随机插入新项目等不确定因素对模具多项目调度的影响，建立了以调度计划变更产生的附加费用最小以及项目加权工期之和最小为优化目标的多目标反应调度模型，并提出了一种改进的多目标微粒群算法IMOPSO进行模型求解。IMOPSO采用一种最优解评估选取方法，并将孤立点搜索策略与精英归档策略相结合，增加了非劣解的多样性与均匀性。通过仿真计算，并分别与文献［18］和文献［24］中的算法进行对比和分析，表明IMOPSO具有良好的性能，能够有效解决模具多项目的动态调度问题。

本文的研究是在Preempt－repeat模式下，以不能强占资源为前提展开的，取得了初步的研究成果。对Preempt－resume模式和可强占资源条件下的模具多项目动态调度的研究将是我们下一步的主要工作。

［1］Herroelen W，Leus R.Project Scheduling under Uncertainty：Survey and Research Potentials［J］.European Journal of Operation Research，2005，65（2）：289－306.

［2］Neumann K.Scheduling of Projects with Stochastic Evolution Structure［M］／／Jozefowska J，Weglarz J.Project Scheduling－Recent Models，Algorithms and Applications.Boston，Mass.，USA：Kluwer Academic Publishers，1999.

［3］Neumann K，Steinhardt U.GERT Networks and the Time－oriented Evaluation of Projects（Lecture Notes in Economics and Mathematical Systems）［M］.New York：Springer－Verlag，1979.

［4］廖仁.模具虚拟企业项目调度研究［D］.广州：广东工业大学，2003.

［5］苏志龙，陈庆新，陈新，等.CPC环境下的模具虚拟企业项目粗规划［J］.机械工程学报，2003，39（1）：38－45.

［6］李英杰，陈庆新，陈新度，等.多属性虚拟企业部分并行协商项目规划［J］.计算机集成制造系统，2005，11（6）：810－817，850.

［7］王延斌，王刚，赵立忠，等.基于蚁群算法的模具制造动态调度研究［J］.计算机集成制造系统，2006，12（7）：1028－1036.

［8］张沙清，陈新度，陈庆新，等.不确定环境下模具制造项目群随机调度研究［J］.计算机集成制造系统，2009，15（7）：1389－1396.

［9］张沙清，陈新度，陈庆新，等.基于多步Q学习的模具制造项目群随机调度算法［J］.中国机械工程，2009，20（12）：1439－1445.

［10］程序，吴澄.粒子群优化算法求解多模式项目再调度问题［J］.计算机集成制造系统，2009，15（1）：97－101.

［11］Lambrechts O，Demeulemeester E，Herroelen W.Proactive and Reactive Strategies for Resourceconstrained Project Scheduling with Uncertain Resource Availabilities［J］.Journal of Scheduling，2008，2（11）：121－136.

［12］Vonder S，Demeulemeester E，Herroelen W，et al.The Trade－off between Stability and Makespan in Resource－constrained Project Scheduling［J］.International Journal of Production Research，2006，44（2）：215－236.

［13］Veldhuizen D，Lamont G.Multi－objective Evolutionary Algorithms：Analyzing the State－ofthe－art［J］.IEEE Transactions on Evolutionary Computation，2000，18（2）：125－147.

［14］李中凯，谭建荣，冯毅雄，等.基于拥挤距离排序的多目标粒子群优化算法及其应用［J］.计算机集成制造系统，2008，14（7）：1329－1336.

［15］Wayne L.运筹学概率模型应用范例与解法［M］.李乃文，崔群法，林细财，等，译.4版.北京：清华大学出版社，2006.

［16］张沙清，陈新度，陈庆新，等.资源不确定环境下模具多项目预测－反应式调度算法［J］.计算机集成制造系统，2010，16（12）：2688－2696.

［17］Coello C，Salzzar M.MOPSO：A Proposal for Multiple Objective Particle Swarm Optimization［C］／／IEEE Proceedings of 2002 Congress on Evolutionary Computation.Washington D.C.，USA：IEEE，2002：1051－1056.

［18］张利彪，周春光，马铭，等.基于粒子群算法求解多目标优化问题［J］.计算机研究与发展，2004，41（7）：1286－1291.

［19］赵志刚，李陶深，杨林峰.求多目标优化问题的粒子群优化算法［J］.计算机工程与应用，2009，45（29）：37－40.

［20］陈黎飞，姜青山，王声瑞.基于层次划分的最佳聚类数确定方法［J］.软件学报，2008，19（1）：62－72.

［21］Abido M A.Environmental／Economic Power Dispatch Using Multi－objective Evolutionary Algorithms［J］.IEEE Transactions on Power Systems，2003，18（4）：1529－1537.

［22］Zitzler E，Deb K，Thiele L.Comparison of Multiobjective Evolutionary Algorithms：Empirical Results［J］.Evolutionary Computation，2000，8（2）：173－195.

［23］周刘喜，张兴华，李纬.一种改进的多目标粒子群优化算法［J］.计算机工程与应用，2009，45（33）：38－41.

［24］王辉，钱锋.基于拥挤度与变异的动态微粒群多目标优化算法［J］.控制与决策，2008，23（11）：1238－1242，1248.

Reactive Scheduling for Multiple Mould and Die Projects Based on Improved Multi－objective Particle Swarm Optimization

Zhang Shaqing Chen Xindu Chen Qingxin Chen Xin
Guangdong University of Technology，Guangzhou，510006

This paper proposed a reactive scheduling algorithm for multiple mould and die projects to deal with multiple stochastic disruptions during projects execution including uncertain renewable resources infeasibilities due to breakdowns，multiple tasks taking longer time than planning and random arrivals of new projects.Firstly，uncertain renewable resources availabilities were analyzed with the theory of birthdead process，and an initial schedule was constructed by using topological sorting method based on priority rules.Then，a multi－objective reactive scheduling model with the optimization objects of minimizing the weighted sum duration of projects and the disruptions cost，defined as the weighted sum of the deviations between the executing schedule before reactive scheduling and a new schedule after reactive scheduling was built，and an improved multi－objective particle swarm optimization was proposed to solve it.Finally，the feasibility and reliability of the reactive scheduling algorithm were analyzed by simulations.

task duration enlarging；uncertain resource availability；reactive scheduling；multi－objective particle swarm optimization

TH166

1004—132X（2011）10—1173—07

2010—10—11

国家高技术研究发展计划（863计划）资助项目（2006AA04Z132）；国 家 自 然 科 学 基 金 资 助 项 目 （50675039，50875051）；广东工业大学青年基金资助项目（20062014）

（编辑 袁兴玲）

张沙清，男，1973年生。广东工业大学机电工程学院博士研究生。主要研究方向为生产计划与控制、网络化制造与信息系统。发表论文10余篇。陈新度，男，1967年生。广东工业大学机电工程学院教授。陈庆新，男，1963年生。广东工业大学机电工程学院教授、博士研究生导师。陈 新，男，1960年生。广东工业大学机电工程学院教授、博士研究生导师。