蜂窝结构缓冲装置的优化设计

尹汉锋 文桂林 马传帅 韩汪利

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082 2.湖南大学特种装备先进设计技术与仿真教育部重点实验室，长沙，410082

蜂窝结构缓冲装置的优化设计

尹汉锋1，2文桂林1，2马传帅1，2韩汪利1，2

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082 2.湖南大学特种装备先进设计技术与仿真教育部重点实验室，长沙，410082

通过简化蜂窝结构轴向压缩的应力–应变曲线，得到了理想的蜂窝结构轴向压缩应力–应变曲线，在该理想曲线的基础上对蜂窝缓冲装置的吸能大小和缓冲力峰值进行了理论计算。为了设计出单位质量吸能量大且缓冲过载小的蜂窝缓冲装置，对蜂窝结构的胞元胞壁厚、胞壁长进行了多目标优化，根据优化结果计算出缓冲蜂窝的最小轴向长度。应用该方法对四支撑腿着陆器中的蜂窝缓冲装置进行了优化设计，并采用试验验证过的Adams多刚体力学模型对优化结果进行了仿真计算，仿真结果表明该优化设计方法能很好地指导着陆器缓冲装置的设计。该方法不仅可以减少试验次数和降低昂贵的试验成本，而且通过多目标优化设计还可以一次满足不同缓冲级别的过载要求。

蜂窝结构；缓冲装置；快速非支配排序遗传算法；优化设计

0 引言

蜂窝材料以其吸能特性稳定和结构质量轻而越来越多地应用在航空航天、汽车以及国防装备等领域。结构轻量化能使航空航天的发射成本大大降低，同时也是未来各大领域的发展方向。所以，如何设计出单位质量吸能量大且缓冲过载小的蜂窝缓冲装置是一个非常值得研究的问题。

蜂窝材料在缓冲过程中一般采用轴向压缩方式进行吸能，本文的蜂窝缓冲装置亦采用该方式进行吸能。蜂窝材料的轴向压缩主要受蜂窝的基体材料和蜂窝元胞尺寸的影响。许多学者对蜂窝材料的轴向缓冲特性进行了研究。早在20世纪60年代，McFarland［1］就计算出了铝蜂窝材料的轴向准静态平均压缩应力。Wierzbicki［2］在超折叠单元的基础上，采用最低能量原理计算出了铝蜂窝材料的轴向准静态平均压缩应力和折叠波长。Kunimota等［3］首先采用理论公式计算了蜂窝结构轴向压缩峰值应力。Zhang等［4］应用板的弹性稳定理论计算了蜂窝结构轴向压缩峰值应力。为了研究蜂窝材料轴向动态冲击特性，Wu等［5］对六种不同类型的铝蜂窝结构分别进行了轴向压缩试验，试验表明，动态平均冲击应力是静态平均压缩应力的1.33～1.74倍。Zhao等［6］采用霍普金森杆试验测得铝蜂窝轴向动态平均冲击应力比其准静态平均压缩应力提高了约40%。除了对金属蜂窝材料的研究外，非金属蜂窝材料也已被许多学者所研究。Wang等［7］采用试验测得了不同类型的纸蜂窝的轴向准静态平均压缩应力和压缩应力峰值，且用理论公式计算了这些纸蜂窝的轴向平均压缩应力和峰值应力，理论结果与试验结果吻合得很好。Wang等［8］研究了环境湿度对纸蜂窝材料轴向压缩应力的影响，提出了不同湿度下的纸蜂窝的吸能公式。根据以上研究，我们也发现蜂窝材料在轴向压缩情况下，压缩过程均由线弹性阶段、屈服阶段、稳态压缩阶段和密实阶段四个阶段组成。

以往研究均表明，蜂窝轴向缓冲吸能大小主要受蜂窝结构基本尺寸（胞元胞壁厚、胞壁长和蜂窝轴向长度等）的影响。所以，对蜂窝结构基本尺寸进行优化以使得蜂窝缓冲装置既能满足缓冲要求又能使其质量最轻具有十分重要的意义。本文采用多目标遗传算法对蜂窝结构胞元胞壁厚和胞壁长进行优化，再根据优化结果计算出缓冲蜂窝的最小轴向长度，从而实现蜂窝缓冲装置的优化设计。

1 蜂窝的轴向压缩特性

蜂窝结构元胞的组成及其基本尺寸如图1a所示，其中，t、D和α分别表示胞壁厚、胞壁长和胞壁夹角。当蜂窝结构受到图1b所示的外界作用力时，即受到轴向压缩时，其典型的应力–应变曲线如图2a实线所示。根据应力–应变曲线的特性，可以把该曲线分为四个阶段：线弹性阶段、屈服阶段、稳态压缩阶段和密实阶段。根据蜂窝结构的应力–应变曲线的特性，可以把未预压缩蜂窝结构的轴向压缩应力–应变曲线简化为图2b中的实线。

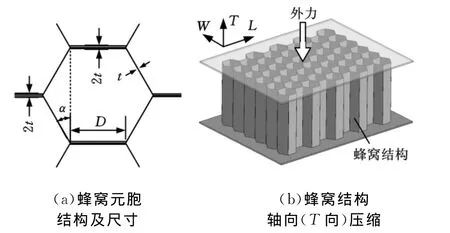
图1 蜂窝元胞结构尺寸及蜂窝结构轴向压缩

在蜂窝结构缓冲过程中，为了消除线弹性阶段初始应力峰值，经常对蜂窝结构进行预压缩处理。预压缩后的蜂窝结构应力–应变曲线如图2a中虚线所示。可以看出，预压缩蜂窝结构的应力–应变曲线与未预压缩蜂窝结构的应力–应变曲线基本相同，仅仅是其屈服阶段消除了，应力–应变曲线直接由线弹性阶段进入到稳态压缩阶段。所以，根据预压缩蜂窝结构的应力–应变曲线特性，我们可以把预压缩蜂窝结构的应力–应变曲线简化为图2c中的实线。

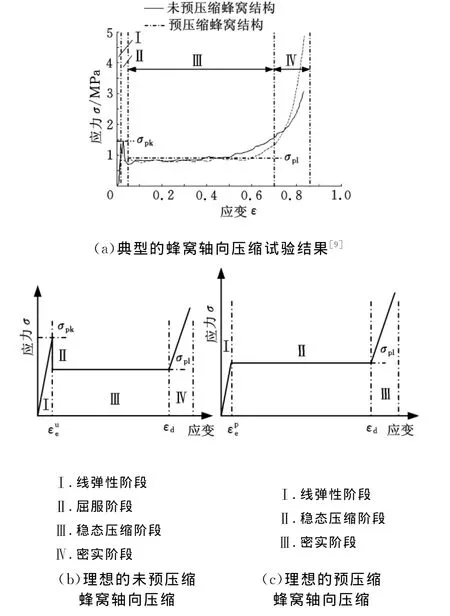
图2 蜂窝结构轴向压缩应力－应变曲线

1.1 准静态轴向压缩各阶段应力

图2a所示为某蜂窝结构的准静态压缩试验的应力–应变曲线，其理想的未预压缩和预压缩轴向应力–应变曲线如图2b和图2c所示。在线弹性阶段，弹性模量Ee为［4］

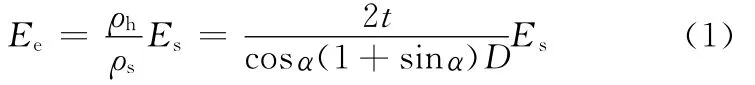
式中，ρh为蜂窝的密度；ρs为蜂窝基体材料的密度；Es为蜂窝基体材料的弹性模量。

当应力–应变曲线从弹性阶段进入屈服阶段时，应力出现峰值σpk，该峰值大小为［4］

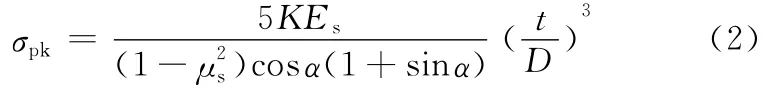
式中，μs为蜂窝基体材料的泊松比；K为结构底部约束系数，在蜂窝底部固定时取K＝5.73［10］，对于不同密度的纸蜂窝结构的轴向压缩工况，K的取值可参考文献［7］。

根据式（1）和式（2），可以得出未预压缩蜂窝结构的弹性应变为

式中，ka和kb为相关系数，可根据试验获得，对于纸蜂窝结构，王志伟［8］等根据试验测得ka＝ 0.818，kb＝－1.689；对于铝蜂窝结构，εd≈0.7［13］。

1.2 动态轴向冲击各阶段应力

由于受质量惯量、基体材料应变率和蜂窝元胞内空气压力等因素［14］的影响，蜂窝结构的动态轴向冲击应力均较静态压缩应力高。根据Harrigan等［9］对金属蜂窝材料的测试结果和Kobayashi等［15］对纸蜂窝材料的测试结果可以发现，蜂窝材料的动态冲击应力峰值和稳态压缩应力均比相应的静态压缩应力大，相应的动态冲击的弹性应变也增大，但动态冲击对密实应变影响不大。在本文中，将采用动态影响系数来计算相应的动态冲击应力。

在动态冲击条件下，蜂窝结构从弹性阶段进入屈服阶段的冲击应力峰值为

1.3 蜂窝轴向动态冲击吸能特性

当蜂窝缓冲装置用于轴向动态冲击吸能时，若蜂窝的截面积为A，则该缓冲装置的冲击力F－压缩量d曲线如图3所示。

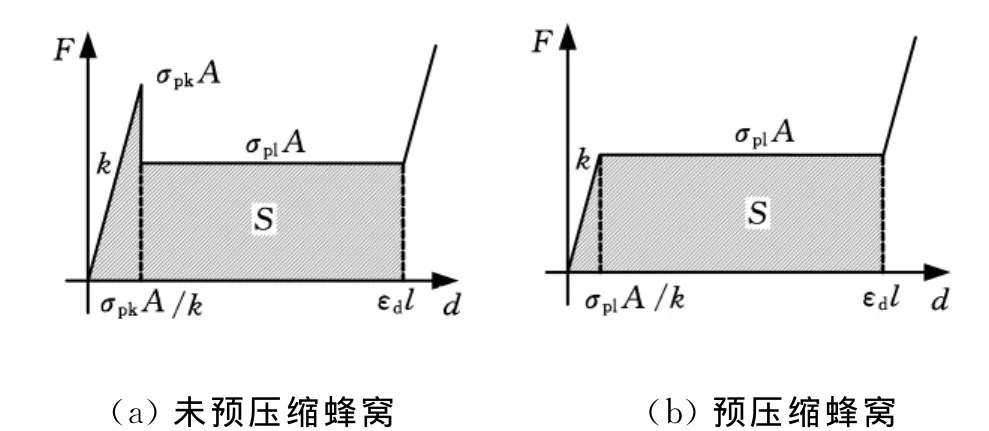
图3 蜂窝缓冲装置冲击力－压缩量曲线

图3a和图3b分别为未预压缩和预压缩蜂窝缓冲装置的冲击力－压缩量曲线，其中阴影部分的面积S即为相应的缓冲装置所能吸收的能量。根据面积计算公式可得未预压缩蜂窝缓冲装置所吸收的能量ENu为

2 蜂窝结构缓冲特性优化

2.1 蜂窝结构缓冲特性优化的定义

设蜂窝结构的密度为ρh，则蜂窝缓冲装置内蜂窝质量m为

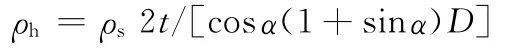
对于蜂窝缓冲结构，我们既希望其缓冲吸能量大，又希望其质量小，所以一般采用单位质量的吸能量（比吸能）来衡量蜂窝结构的吸能特性。对于未预压缩蜂窝，其比吸能SEA的大小为

2.2 优化算法

为了求解式（16）所示的优化设计问题，本文采用多目标遗传算法中的快速非支配排序遗传算法（NSGA－Ⅱ）进行求解。

NSGA－II算法是一种目前应用十分广泛的多目标遗传算法，该算法由Deb等［16］于2000年提出，该算法采用了非支配排序、精英保留策略和无参数小生境操作，克服了传统非支配排序遗传算法（non－dominated sorting genetic algorithm，NSGA）计算复杂度高、算法执行速度慢且需要指定共享半径等问题。NSGA－Ⅱ算法的流程如图4所示，其中，N为种群大小，gmax为遗传最大代数。利用该算法可以求得蜂窝结构比吸能与缓冲应力峰值的Pareto最优解集。

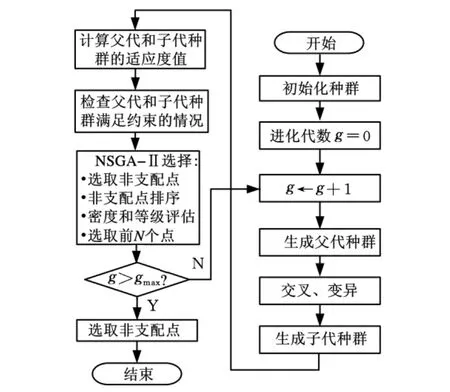
图4 NSGA－Ⅱ算法流程图

3 蜂窝结构缓冲装置的优化设计

在实际工程中，当蜂窝结构用于吸收冲击物的动能时，必须满足吸能和缓冲过载的要求，因此蜂窝的优化设计流程如图5所示。其中，CU和Ca分别为设计中的能量安全系数和过载安全系数，均取大于等于1的常数。

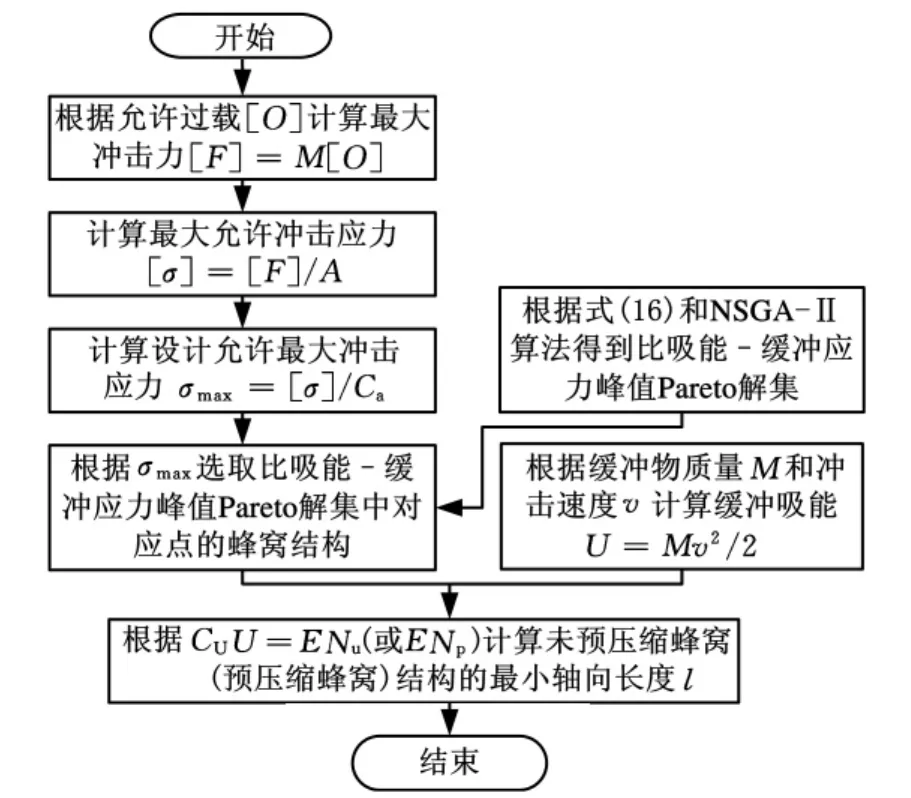
图5 缓冲蜂窝优化设计流程图

4 缓冲蜂窝优化设计的应用算例

4.1 算例条件

如图6所示，某四支撑腿着陆器总体质量M＝1200kg，以v＝4m／s的速度垂直降落到地面上。着陆器采用主缓冲筒内的正六边形铝蜂窝轴向压溃进行缓冲吸能，铝蜂窝在使用前进行了预压缩处理。在设计中要求总蜂窝缓冲力与主体质量的比值小于允许过载。铝蜂窝基体材料为AA6060 T4，其主要力学特性为［11］：密度ρs＝2700kg／m3，弹性模量Es＝68.2GPa，泊松比μ＝0.3，屈服强度σy＝80MPa，极限强度σu＝173MPa，应变硬化指数n＝0.23。蜂窝在动态冲击下稳态阶段的影响系数［17］取为1.4，主缓冲筒内缓冲蜂窝的截面为圆形，圆形蜂窝半径r＝0.06m。蜂窝特性优化变量为蜂窝元胞的胞壁厚t和胞壁长D，各变量范围为：0.03mm≤t≤0.08mm，2mm≤D≤10mm。取能量安全系数CU＝1.1，过载安全系数Ca＝1.1。

4.2 优化结果及分析

根据式（16），该主缓冲筒内缓冲蜂窝的缓冲特性优化可写为如下形式：

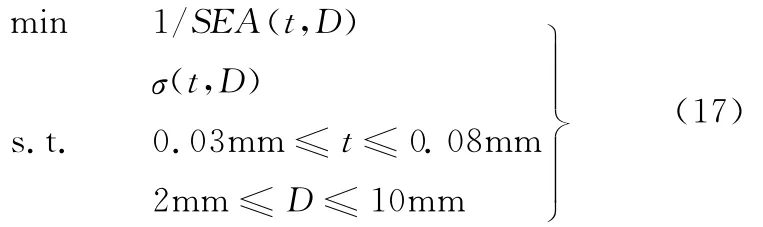
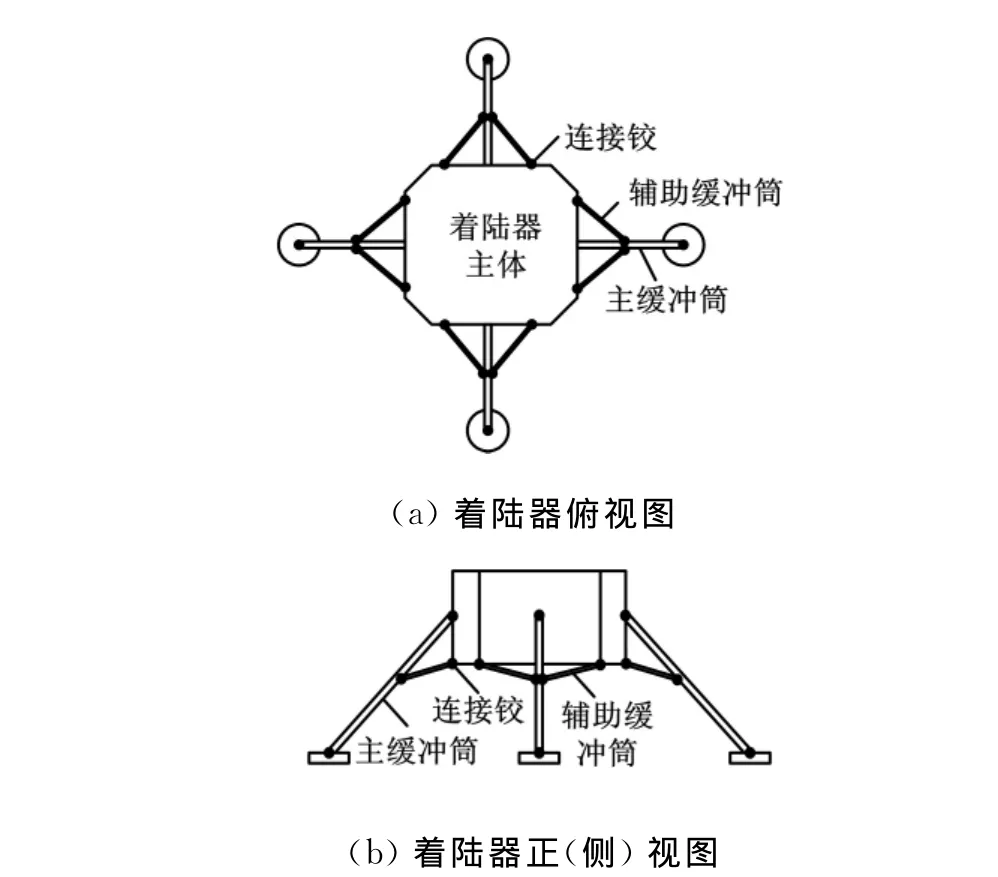
图6 四支撑腿着陆器示意图

采用NSGA－Ⅱ算法对式（17）进行求解，在NSGA－Ⅱ算法中，设置种群大小为200，交叉概率为0.9，变异概率为0.2，交叉和变异分配指数均为20，经过1000次遗传迭代后的Pareto最优解如图7所示。

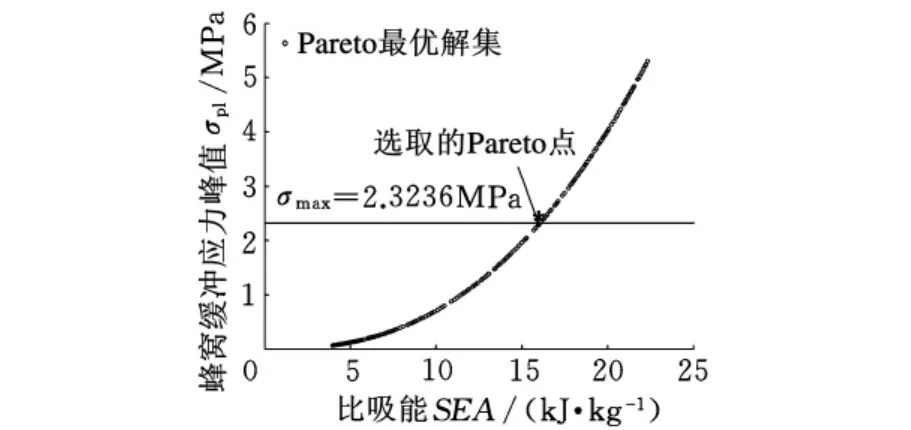
图7 缓冲蜂窝比吸能－缓冲应力峰值Pareto解集

设着陆器的允许过载［O］＝0.098N，根据图5中的计算公式可得允许最大冲击应力σmax＝2.3236MPa。所以，选取图7中的Pareto点对应的蜂窝结构作为主缓冲筒内的缓冲蜂窝，该点对应的蜂窝尺寸为t＝0.0546mm，D＝2.2558mm，再根据能量平衡公式CUU＝ENp及式（12）可得蜂窝最小轴向长度l＝143.7mm。

同理，可以计算允许过载［O］为0.147N和0.196N的蜂窝结构尺寸如表1所示。

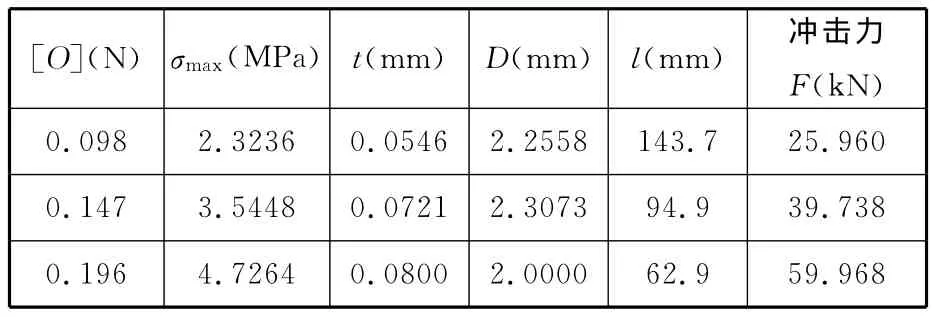
表1 优化设计的主缓冲筒缓冲蜂窝特性

4.3 优化结果的验证

图8 着陆器模型及计算结果

为了验证优化结果的可行性，采用Adams软件二次开发方式建立了该四腿着陆器的多刚体力学参数化模型［18-19］，如图8a所示。为了验证该多刚体力学模型，我们进行了相关工况试验，试验模型如图8b所示。图8c所示为该多刚体力学模型计算的着陆器主体质心加速度与相应工况试验的主体质心加速度曲线，从图8可以看出，两者吻合得很好。应用验证后的力学模型计算表1中0.098N允许过载对应优化结果的着陆器主体质心加速度曲线如图9所示，计算结果显示，经过优化设计后，该着陆器不仅能满足过载要求，而且通过铝蜂窝的轴向压缩也能很好地吸收着陆器的冲击动能。

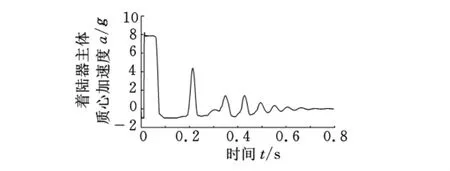
图9 优化设计工况着陆器质心加速度

5 结论

为了设计出单位质量吸能量大且缓冲过载小的蜂窝缓冲装置，本文对蜂窝结构的胞元胞壁厚、胞壁长进行了多目标优化，利用优化结果结合能量守恒原理计算出了缓冲蜂窝的最小轴向长度，从而实现了蜂窝缓冲装置的优化设计。同时，应用该方法对四支撑腿着陆器中的主缓冲筒内铝蜂窝进行了优化设计。最后运用试验验证后的Adams多刚体力学模型对优化的着陆器蜂窝缓冲装置的缓冲过程进行了分析，分析表明该缓冲装置能很好地满足工程设计要求。

应用本文的蜂窝缓冲装置优化设计方法可以对各种蜂窝缓冲装置如航天器蜂窝缓冲装置及装备空投蜂窝缓冲装置等进行优化。该蜂窝缓冲装置优化设计方法不仅可以减少试验次数和昂贵的试验成本，而且通过多目标优化设计可以一次满足不同缓冲级别的过载要求，对产品的实际工程设计具有指导意义。

［1］McFarland R K.Hexagonal Cell Structures under Post－buckling Axial Load［J］.AIAA Journal，1963，1（6）：1380－1385.

［2］Wierzbicki T.Crushing Analysis of Metal Honeycombs［J］.International Journal of Impact Engineering，1983，1（2）：157－174.

［3］Kunimoto T，Yamada H.Study on the Buffer Characteristics of the Honeycomb Sandwich Construction under Dynamic Loading［J］.Journal of Light Metals，1987，37（5）：327－331.

［4］Zhang J，Ashby M F.The Out－of－plane Properties of Honeycombs［J］.International Journal of Impact Engineering，1992，34（6）：475－489.

［5］Wu E B，Jiang W S.Axial Crush of Metallic Honeycombs［J］.International Journal of Impact Engineering，1997，19（5／6）：439－456.

［6］Zhao H，Gary G R.Crushing Behaviour of Aluminium Honeycombs under Impact Loading［J］.International Journal of Impact Engineering，1998，21（10）：827－836.

［7］Wang D M，Wang Z W.Out－of－plane Compressive Properties of Hexagonal Paper Honeycombs［J］.Chinese Journal of Mechanical Engineering，2007，20（2）：115－119.

［8］Wang Z W，E Y P.Mathematical Modelling of Energy Absorption Property for Paper Honeycomb in Various Ambient Humidities［J］.Materials ＆ Design，2010，31（7）：4321－4328.

［9］Harrigan J J，Reid S R，Peng C.Inertia Effects in Impact Energy Absorbing Materials and Structures［J］.International Journal of Impact Engineering，1999，22（9／10）：955－979.

［10］Roark R J，Young W C.Formulas for Stress and Strain［M］.5th Edition.Tokyo：McGraw－Hill Kogakusha，1975.

［11］Santosa S P，Wierzbicki T，Hanssen A G，et al.Experiment and Numerical Studies of Foam－filled Sections［J］.International Journal of Impact Engineering，2000，24（5）：509－534.

［12］Liu R Q，Luo C J，Deng Z Q，et al.Design and Selection of Aluminum Foam for Impact Damper of Legged Lunar Lander［C］／／The 2nd International Symposium on Systems and Control in Aeronautics and Astronautics.Shenzhen，China，2008：1－6.

［13］Hexcel Corporation.HexWeb Honeycomb Attributes and Properties［EB／OL］.（1999－11－9）.http：／／www.hexcel.com／NR／rdonlyres／96FE250C－7BB1－4295－82C4－461A31CC97A0／0／HexWeb HoneycombEnergy AbsorptionBrochure.pdf

［14］Zhao H，Elnasri I，Abdennadher S.An Experimental Study on the Behaviour under Impact Loading of Metallic Cellular Materials［J］.International Journal of Mechanical Sciences，2005，47（4／5）：757－774.

［15］Kobayashi H，Daimaruyam M，Kobyashit T.Dynamic and Static Compression Tests for Paper Honeycomb Cores and Absorbed Energy［J］.Muroran Inst.of Technology，1998，41（3）：338－344.

［16］Deb K，Agrawal S，Pratap A，et al.A Fast and Elitist Multiobjective Genetic Algorithm：NSGA－Ⅱ［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：182－197.

［17］Langseth M，Hopperstad O S.Static and Dynamic Axial Crushing of Square Thin－walled Aluminium Extrusions［J］.International Journal of Impact Engineering，1996，18（7／8）：949－968.

［18］朱汪，杨建中.月球探测器软着陆机构着陆腿模型与仿真分析［J］.宇航学报，2008，29（6）：1723－1728.

［19］陈金宝，聂宏，赵金才，等.月球探测器软着陆缓冲机构着陆性能分析［J］.宇航学报，2008，29（6）：1729－1732.

Optimization Design of Cushion Instrument of Honeycomb Structure

Yin Hanfeng1，2Wen Guilin1，2Ma Chuanshuai1，2Han Wangli1，2
1.State Key Laboratory of Advanced Design and Manufacture for Vehicle Body，Hunan University，Changsha，410082 2.the Key Laboratory of Advanced Design and Simulation Techniques for Special Equipment，Ministry of Education，Hunan University，Changsha，410082

After simplifying the crushing strain－stress curve of honeycomb structure under axial loading，an ideal crushing strain－stress curve was obtained.Based on the ideal crushing strain－stress curve，the energy absorbed by the cushion instrument of honeycomb structure and the peak crushing force were calculated.In order to design a cushion instrument of honeycomb structure that has the biggest energy absorption capacity per unit mass and has the minimum cushion overload，a cell wall thickness and width of the honeycomb structure were optimized by using multi－objective optimization method.According to the optimization results，the minimum axial length of the honeycomb structure can be calculated.Then，the honeycomb cushion instrument installed in the four legged lander was optimized using this method.The optimization results were verified by employing the multi－body dynamics model established in Adams software.The simulation results indicate that this optimization method can direct the design of the landing instrument very well.This method can reduce the times and the cost of the tests，and meets the cushion demands of different overloads.

honeycomb structure；cushion instrument；non－dominated sorting genetic algorithmⅡ（NSGA－Ⅱ）；optimization design

TB535.1

1004—132X（2011）10—1153—06

2010—05—13

教育部科技创新工程重大项目培育资金资助项目（708067）

（编辑 苏卫国）

尹汉锋，男，1982年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。主要研究方向为薄壁结构的耐撞性设计。文桂林，男，1970年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。马传帅，男，1983年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。韩汪利，男，1986年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。