机电集成电磁式谐波摩擦传动柔轮的受力与变形分析

任玉波 许立忠 梁永丽，2

1.燕山大学，秦皇岛，066004 2.里仁学院，秦皇岛，066004

机电集成电磁式谐波摩擦传动柔轮的受力与变形分析

任玉波1许立忠1梁永丽1，2

1.燕山大学，秦皇岛，066004 2.里仁学院，秦皇岛，066004

针对电磁式谐波摩擦传动柔轮在磁场中发生变形，使气隙随时改变这一现象，引入气隙函数的概念，并根据薄壳弹性变形理论，将传动的柔轮简化为圆柱壳体，建立了在电磁场力作用下柔轮的静力分析模型。该方法由于考虑了柔轮的变形导致的磁密的变化，能够更确切地描述电机径向电磁力的特性及柔轮的受力与变形规律，为电磁式谐波电机的设计及强度校核提供了更为可靠的理论依据。

机电集成；谐波传动；柔轮；磁场力；变形

0 引言

谐波传动是指一类利用中间挠性构件的弹性变形来实现运动或动力传递的传动装置的总称，在军用和民用工业上获得了广泛的应用［1－4］。电磁式谐波传动是将旋转磁场与谐波传动相结合而成的一种新型装置，它兼有电机和机械减速器的功能，特点是体积小、重量轻、结构简单而紧凑、传动比大、惯量非常小、响应速度快、精度高、可靠性高。电磁式谐波传动分齿轮传动和摩擦传动两种，电磁式谐波齿轮传动在提出时被称为“无减速器驱动的具有挠性转子的低速电动机”。这种传动装置除了具有以上优点，还有很多不足：如起动力矩较大，而且速比越小越严重；在传递运动中，柔轮会发生周期性弹性变形，因此柔轮上的齿容易产生疲劳破坏；齿轮模数很小，但要求精度很高［5］。而谐波摩擦传动由于是靠摩擦传动的，刚轮和柔轮上没有齿，在传动的过程中，除了响应速度快、传递力矩大，构件还不容易损坏，机器寿命长、噪声小。

但是，电磁式谐波摩擦传动是一个涉及电磁学、力学、机械学和控制技术等多学科的复杂系统，目前还鲜见此方面的研究报道，而电磁式谐波摩擦传动在航空航天、电子工业和机床工业中具有很好的应用前景和发展空间，因此本文重点研究电磁式谐波摩擦传动。

1 电磁式谐波摩擦传动的工作原理

1.1 谐波摩擦传动原理

谐波传动有三个基本构件：柔轮、刚轮和波发生器。三个构件中可任意固定一个，其余两个一个为主动件，另一个为从动件。柔轮在波发生器的作用下发生波动变形，柔轮上所有的点都具有径向位移，谐波传动的工作原理就是利用挠性构件的弹性变形来达到运动转换的目的。根据弹性壳体理论，当柔轮变形时，其径向位移w必将伴随着产生切向位移s，从而实现了与位移密切相关的速度d w／d t（径向速度）与d s／d t（周向速度）之间的运动转换，即当柔轮发生波动变形时，将使柔轮上所有的点都具有周向速度和径向速度，且周向速度在波峰处达到最大。由于有了径向位移，致使柔轮与刚轮沿波峰相接触，从而产生正压力，又由于柔轮上的点具有周向速度，所以在柔轮和刚轮的接触处便产生了摩擦力，使得柔轮和刚轮之间产生切向相互作用力。所以当柔轮固定时，刚轮转动，刚轮与波发生器的转向相同；当刚轮固定时，柔轮转动，但柔轮与波发生器的转向相反。

1.2 电磁式谐波摩擦传动

图1所示为刚轮固定，波发生器主动，柔轮从动时系统的结构示意图。

图1 电磁式谐波摩擦传动结构示意图

传动的柔轮2是半径为r、厚度为t的杯状金属圆柱，柔轮与刚轮和电磁铁芯绕组之间是厚度为δ的空气隙。柔轮在未变形时的原始剖面呈圆形，柔轮在旋转磁场的作用下会发生变形，即将磁场力顺序地施加于不同的相对应的两个扇区内，柔轮会在相应的位置发生变形，与刚轮接触。由于变形的周期性，柔轮会因此而反向转动起来，在柔轮输出轴上可得到经过谐波减速的低速输出运动。用nE表示旋转磁场的旋转方向，nS表示柔轮的旋转方向，则系统在旋转磁场变化一个周期内的运动情况如图2所示。柔轮方向与磁场方向相反，传动比为

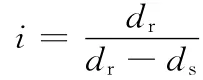
式中，dr为柔轮外径；ds为刚轮内径。

由于空气隙很薄，所以传动比i一般很大。

2 磁场力的计算

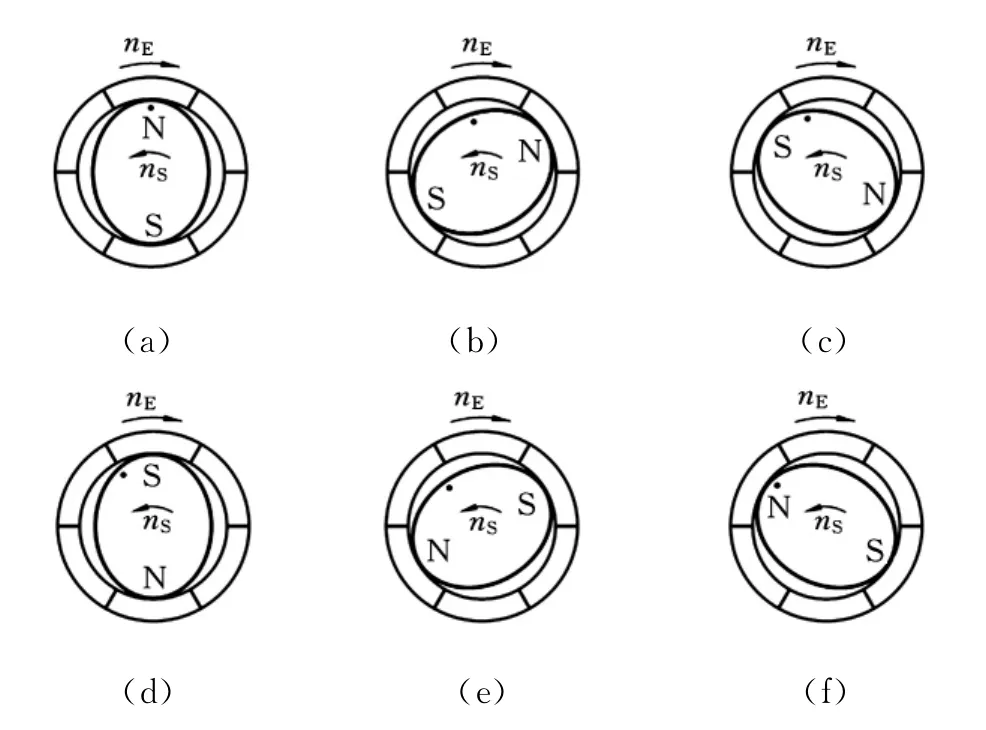
图2 柔轮运动示意图

在谐波传动中，柔轮的受控弹性变形分析非常重要，对于电磁式谐波摩擦传动来说更是如此。由于电磁力是一种场力，分布作用于柔轮上，因此对于柔轮来说，没有刚性元件支撑，其变形形状完全由磁场分布状况决定。

2.1 假设条件

（1）薄壳的小挠度变形理论。谐波传动中，柔轮的最大径向变形与其厚度相当，并且远小于直径，因此符合小变形条件，在中面上，应变为零。

（2）似稳电磁场理论［6］。假定电磁场旋转规律为正弦函数，从而柔轮上受到的电磁力与时间无关，于是柔轮变形形状与磁场作用力的相对位置保持不变。

（3）体力及面力均可简化为作用在中面上的载荷。

2.2 三相分布绕组的合成磁势

电磁式谐波摩擦传动中产生旋转磁场的方式有两种：一种是对多相绕组依次控制导通来产生脉冲的旋转磁场；另一种是对多相绕组通入交流电获得一个连续旋转的正弦电磁场。本文以三相绕组的连续旋转磁场为例，其中每一相都是整距集中单层绕组，三个相绕组在空间位置上彼此互相距离120°。

当三相绕组通入对称的三相交流电时，三相合成磁势为一个幅值不变的行波，其角速度为ω＝2πf。

由于三相绕组在空间互相间隔120°，因此它们所产生的基波磁势在空间也有120°的位移；在负载对称的条件下，三相电流在时间上彼此也相差120°，因此三个脉冲磁势在时间上也有120°的相位移。考虑到这两个特点，三个脉动磁势的基波分量可以写成：

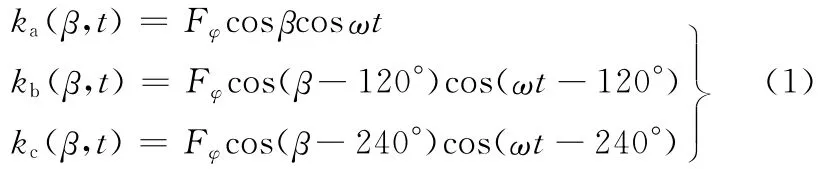
式中，Fφ为合成磁势的基波幅值；β为空间转角。

式（3）表示在某一固定瞬时，三相合成磁势在空间呈余弦分布。

2.3 气隙长度函数

三相绕组基波磁势在气隙产生的磁感应强度为［7］式中，B1为在气隙产生的磁感应强度幅值。

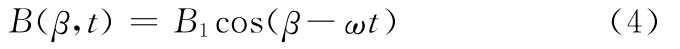
对于谐波电机，由于采用柔性转子，因此气隙长度为一个随电枢表面变化的函数，而不是常数，如图3所示。

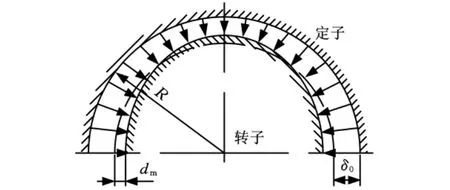
图3 气隙长度

2.4 径向电磁力的计算

当仅考虑基波磁感应强度作用时，柔轮单位面积上所受到的径向电磁力为

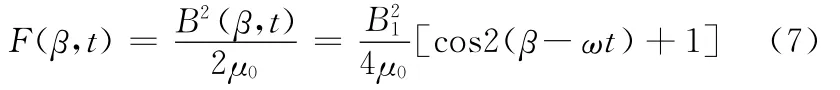
式（7）表示柔轮所受到的力为一旋转的以B1为幅值的分布力波，其旋转速度与三相旋转磁势相同，波形为二次余弦波。当三相绕组极对数为1时，径向电磁力沿圆周气隙分布及展开如图4、图5所示。

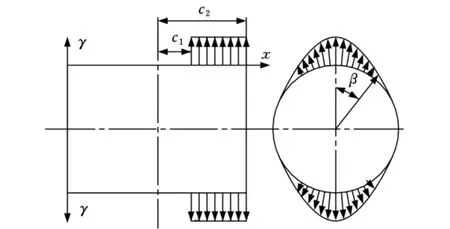
图4 柔轮上所受径向电磁力在某一瞬时的分布

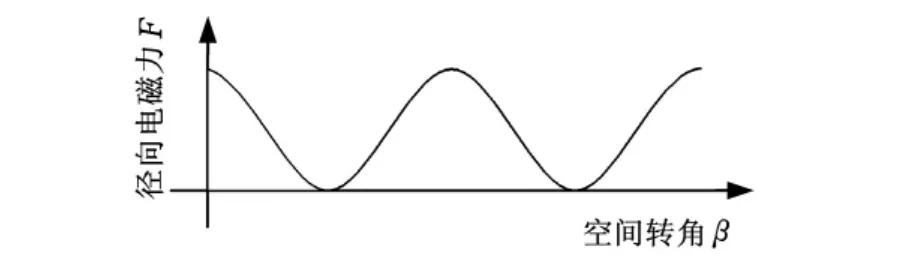
图5 柔轮横截面所受径向电磁力的展开波形

3 柔轮的径向变形分析

3.1 柔轮受径向电磁场分布力产生的径向变形

谐波传动就是依靠柔轮的周期性径向弹性变形来实现的，因此本文仅研究柔轮的径向变形，不考虑轴向及周向变形。

当柔轮壳体受一对径向集中力作用时，如图6所示，壳体上中面的径向位移可表示为［8］

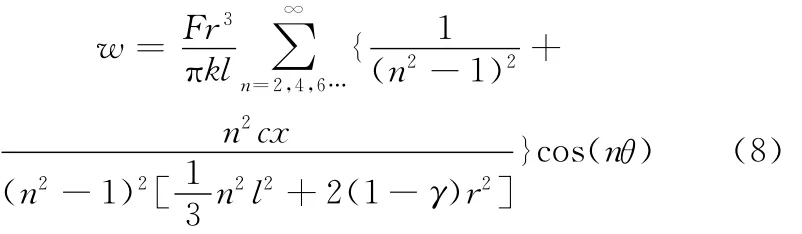
式中，k为壳体的抗弯刚度；γ为泊松比。

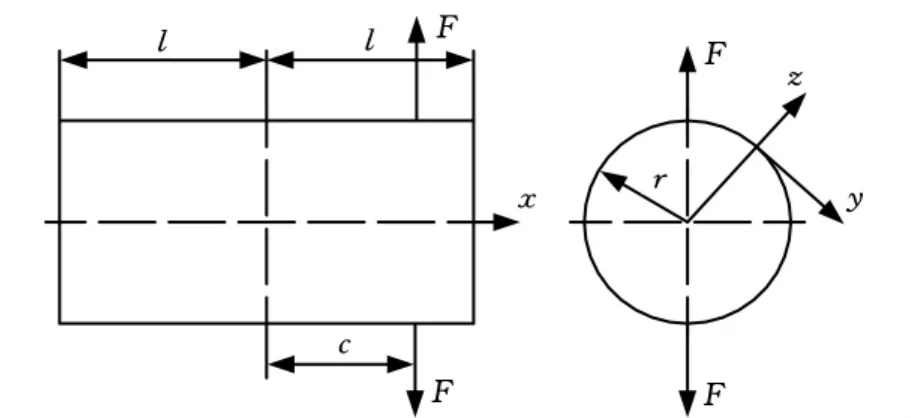
图6 受一对径向集中力时位移的计算模型

对于柔轮壳体上作用有图4所示的分布力的情况，利用叠加原理［9］，根据式（8）可求得柔轮中面上任一点的径向位移：

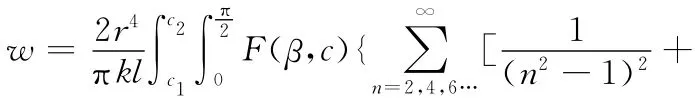
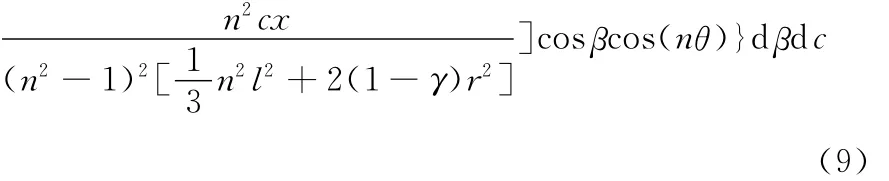
3.2 边界条件

式（8）和式（9）是用来计算两端自由的薄壁圆柱壳体位移的，而实际上柔轮壳体为一端封闭的杯状壳体，则相应的边界条件为w＝0｜x＝x0，即当

4 算例及分析

当仅考虑空载磁场下的柔轮受力状态（相当于去掉刚轮，柔轮不被限位，可以自由变形），在额定条件下（电压220V，电流0.53A），且基波气隙磁密为0.4857T时，根据式（7）计算磁场区域的作用力载荷值，得到磁场中心最大径向位移沿轴向的分布情况，如图7所示。图7中还显示了因电压改变导致电流也发生变化时的结果。

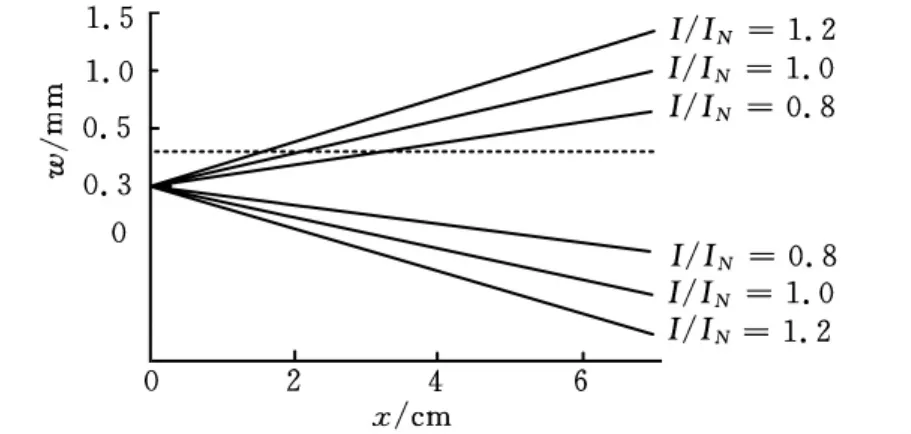
图7 最大径向位移沿轴向的分布情况

图7的这种状态不是实际存在的，但我们可以从中了解磁场力的作用情况。当柔轮的变形为0.3mm时，将受到刚轮的限位，阻止其变形，因而柔轮将受到一个反力的作用，这个力的大小反映了磁场力所能提供输出力的大小。表1列出了柔轮正负变形量与电流相对值的关系，可以看出，在谐波电机的工作状态下，柔轮母线的变形情况基本是条直线。柔轮变形形状不是理想椭圆，在短轴处的变形幅值比长轴处的变形幅值要小。

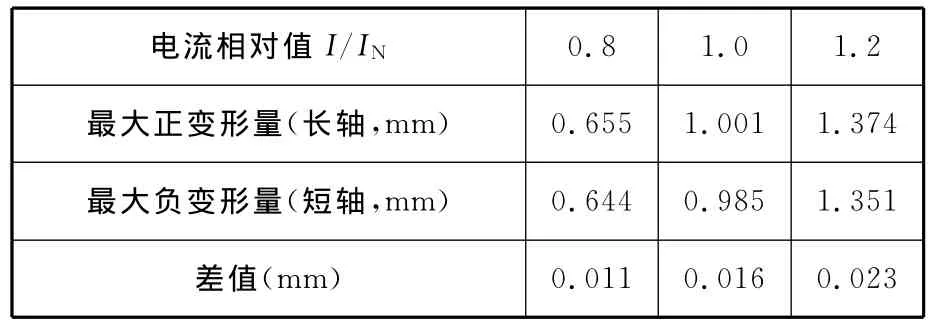
表1 电流与变形

5 结论

阐述了机电集成电磁式谐波摩擦传动的工作原理，分析了柔轮在磁场中因发生变形，使气隙随时改变这一现象。引入了气隙函数的概念，并将谐波传动中产生变形的柔轮简化为圆柱壳体，对旋转磁场作用于柔轮的径向力进行了计算分析。给出了磁场对柔轮作用力的大小和分布规律，通过算例讨论了柔轮在磁场中最大径向位移沿轴向的分布情况，给出了因电压改变导致电流也发生变化时的结果。该方法由于考虑了柔轮的变形导致的磁密的变化，能够更确切地描述电机径向电磁力的特性及柔轮的受力与变形规律，为解决电磁式谐波传动的分析与计算问题提供了依据。

［1］Jacobsen S C，Price E H，Wood J E，et al.The Wobble Motor：an Electrostatic，Planetary－armature，Microactuator［C］／／IEEE Micro Electro Mechanical Systems Workshop.Salt Lake，1989：17－24.

［2］Trimmer W，Jebens R.Harmonic Electrostatic Motors［J］.Sensors and Acutators，1989，20（1／2）：17－24.

［3］Thielicke E，Obermeier E.Microactuators and Their Technologies［J］.Mechatronics，2000，10（4／5）：431－455.

［4］Judy J W.Microelectromechanical System（MEMS）：Fabrication，Design and Applications［J］.Smart Mater Struct.，2001，10（6）：1115－1134.

［5］吴忠，刘元度.谐波传动的工程应用研究［J］.航空精密制造技术，2005，41（4）：23－25.

［6］Straton J A，Electromagnetic Theory［M］.McGraw－Hill，1941.

［7］舒波夫 NΓ，沈官秋，译.电机的噪声和振动［M］.北京：机械工业出版社，1980.

［8］铁摩辛柯S，沃诺斯基S.板壳理论［M］.北京：科学出版社，1977.

［9］张崑.电磁式谐波传动研究［D］.大连：大连理工大学，1989.

Force and Deformation Analyses for Flexspline of an Electromechanical Integrated Electromagnetic Harmonic Friction Drive

Ren Yubo1Xu Lizhong1Liang Yongli1，2
1.Yanshan University，Qinhuangdao，Hebei，066004 2.LiRen College，Qinhuangdao，Hebei，066004

In view of the phenomenon that an electromagnetic harmonic friction driving flexspline will deform in a magnetic field，this deformation will change the airgap at any moment，a concept of airgap function was introduced.And based on thin－shelled elastic deformation theory，simplifying the driven flexspline to a column shell，a model was built and used to analyse the static force of flexspline affected by electromagnetism.Due to this method has considered flux density change caused by flexspline formation，it can precisely describe the characteristics of the radial electromagnetic force，the force and deformation rule of flexspline.It provides a more reliable theoretical basis for harmonic electromagnetic motor structure design and strength check.

electromechanical integration；harmonic drive；flexspline；electromagnetism force；deformation

TH132

1004—132X（2011）10—1169—04

2010—07—22

（编辑 袁兴玲）

任玉波，女，1963年生。燕山大学机械工程学院副教授。主要研究方向为现代机械传动及机电集成系统。发表论文30余篇。许立忠，男，1962年生。燕山大学机械工程学院教授、博士研究生导师。梁永丽，女，1980年生。燕山大学里仁学院讲师。