端部初始燃面可变的星孔火箭装药燃烧特性

牛公杰，钱建平，刘荣忠

（南京理工大学机械工程学院，江苏 南京210094）

引 言

传统的小型自由装填式固体火箭发动机在设计时，为了控制药柱的燃烧面积，通常用包覆层将药柱的部分表面进行包覆［1］。根据所设计的装药结构几何尺寸，按照平行层燃烧理论可准确地计算出燃烧过程中不断变化的燃面面积，进而计算出火箭发动机内弹道诸元。对于采用星孔装药的小型自由装填式固体火箭发动机，常用的包覆措施是将药柱侧面、上、下端面包覆；但也有采取仅将药柱侧面包覆，而上下端面不包覆的方法，通过药柱端面和垫片间的间隙使药柱端面在火箭发动机工作过程中也参与燃烧，进一步提升火箭发动机性能［2］。

星孔火箭装药的端部初始燃烧面积对火箭发动机性能有着重要影响。而间隙的大小又决定了端部初始燃面的变化规律。装药端部参与燃烧虽然有助于提升火箭发动机性能，但也给端部初始燃面的计算带来困难，无法使用经典的燃面计算理论进行描述和计算［3］。本研究通过引入端面燃烧参与度和端面等效燃烧厚度的方法来解决燃面计算问题，并结合试验条件推导出了燃面面积经验计算公式，得出温度对火箭发动机性能的影响规律和可用于指导实际工程应用的结论。

1 燃面计算方法

1.1 基本假设

火箭发动机装药在点火具作用下，药柱星孔全面瞬时点燃，高温燃气和火焰会窜入药柱端面和垫片之间的间隙并逐渐点燃端面，过程较为复杂，难以用量化的方式描述，应用传统的燃面计算理论无法描述燃面变化规律和计算燃面面积，需引入新的方法解决燃面计算问题。

根据药柱燃烧特点，可将燃面计算过程分为星孔燃面面积计算和端部燃面面积计算两部分，并作如下假设：（1）在点火压强作用下星孔全面瞬时点燃；（2）忽略药柱的侵蚀燃烧效应；（3）星孔燃烧遵循平行层燃烧定律，燃面沿起始表面各点的法线向内部推移。

对于星根圆角化的星孔装药，星孔燃烧过程可分为4个阶段［4］，即：（1）星根圆角消失前，星边周边长为s1，单位：m；（2）星边消失前，星边周边长为s2，单位：m；（3）星边消失后，星边周边长为s3，单位：m；（4）余药阶段燃烧阶段，星边周边长为s4，单位：m。

图1为星孔装药结构示意图。其中左侧为星孔药柱端面燃烧示意图，右侧为药柱沿轴向的剖面图。端部燃烧是个极其复杂的过程，为简化计算，作如下4点假设：（1）药柱燃烧到t时刻时，一个端面的总面积为Stt，单位：m2，且：Stt=πD2／4-Ap，D为药柱外径，单位：m，Ap为药柱星孔通气面积，单位：m2；（2）药柱燃烧到t时刻时，一个端面参与燃烧的面积为Stb，单位：m2，并且假设燃面Stb平行于药柱初始端面；（3）引入端面燃烧参与度α，表示一个端面当前参与燃烧的面积Stb与当前端面总面积Stt之比，即：且0≤α≤1；（4）根据药柱质量守恒原则，引入端面等效燃烧厚度et，单位：m。

1.2 端面燃烧参与度α

药柱端面和垫片之间的间隙是影响α变化过程的主要因素。发动机的零件加工误差和装配误差直接影响药柱端面与垫片间初始间隙的大小，而温度变化则会改变初始间隙的大小。一般发动机壳体的热膨胀系数远小于药柱的热膨胀系数，而垫片的厚度与发动机药室高度和药柱高度相比很小，故当发动机壳体、药柱和垫片三者经历相同的温度变化后，药柱高度变化量要远大于发动机药室高度变化量和垫片高度变化量，所以间隙的变化主要取决于药柱的高度变化量。以发动机在常温状态下装配产生的间隙为基准，当发动机在高温状态下，间隙变小，在低温状态下，间隙变大。

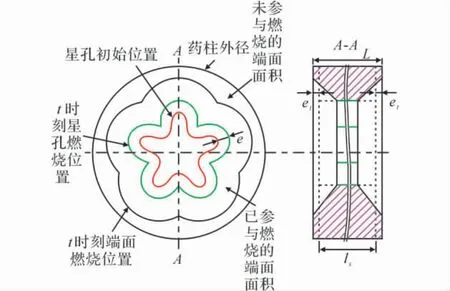
图1 星孔装药结构示意图Fig.1 Schematic diagram of star shaped rocket grain

从定性的方面分析，药柱端面与垫片之间的间隙越大、燃烧室压强p越大、药柱初始温度越高、药柱的长径比L／D越大，则端面点燃速度越快，端面全面参与燃烧所用的时间越短，反之亦然。因药柱端面随着药柱燃烧时间的增加而逐渐点燃，选取时间t为自变量，考虑到α的变化过程与药柱燃烧室压力p、药柱长度L、初始温度T、药柱直径D等因素密切相关，α可表示为：

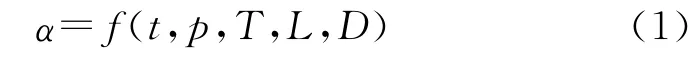
根据试验，发现对于长径比在1.3左右、特征长度与肉厚比在0.5左右、星角数为5的星孔装药，其端面正常逐渐参与燃烧时，α呈幂函数形式变化。研究结合试验条件和测试结果，推导出了不同情况下α的经验计算公式。

（1）常温和低温情况下，药柱端面在点火初始时刻即可正常参与燃烧的经验公式为：

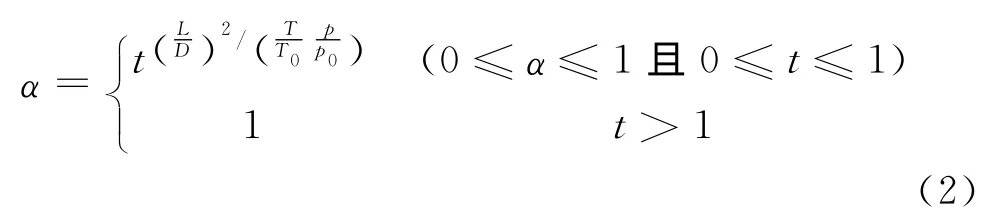
式中：t为燃烧时间，s；T为药柱初始温度，K；T0为参考基准温度，K，T0=273.15K；p0为参考基准压力，Pa，p0=106Pa。

（2）高温情况下，由于药柱端面与垫片的间隙变小或消失，初期燃烧室内压力相对较小，燃气不能顺利与端面接触，药柱端面在初始燃烧阶段燃烧参与程度较小，当燃烧进行到某一临界时刻t0（t0＜1），燃烧室内压强升高到某一个临界值时，燃气急剧窜入间隙，迅速全面点燃尚未参加燃烧的端面，α的经验公式为：

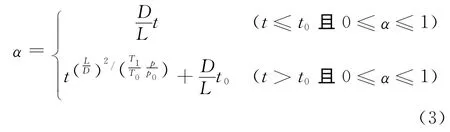
式中：t0为临界时刻，s，其大小根据具体试验条件确定。

1.3 端面等效燃烧厚度et

由于端面燃烧参与度系数α的引入，为保证药柱燃烧质量守恒，需将端面燃烧厚度做等效处理。在端面从起始燃烧到全面燃烧的过程中，即当0≤α＜1时，设在dt时间微元内一个端面燃烧掉的质量微元为dmt，它应该等于当前时刻的端面参与燃烧的燃烧面积Stb、燃烧厚度微元de和推进剂密度ρp三者的乘积，即：

式中：mt为端面燃烧掉的质量，单位：kg。

将质量微元dmt等效由当前端面面积为燃面烧去的质量，则质量微元dmt应等于当前端面面积Stt、端面等效燃烧厚度微元det和推进剂密度ρp三者的乘积，即：

根据（4）、（5）两式相等，可导出端面等效燃烧厚度et的微分方程：

记端面面积全部参与燃烧瞬时时刻为tα1，当t≥tα1时，端面面积全部参与燃烧，Stb=Stt，α=1。

式中：a为燃速系数，m／（s·Pan）；n为燃速指数。

由（7）式即得到端面等效燃烧厚度计算公式

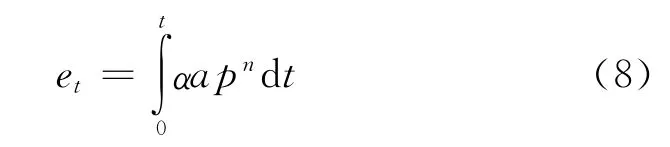
1.4 总燃面计算

总燃面面积应等于星孔燃面面积加上端部燃面面积。星孔燃面面积根据平行层燃烧定律计算，药柱星孔长度应等于药柱初始长度L减去两个端面的等效燃烧厚度2et，则星孔燃面面积计算公式：

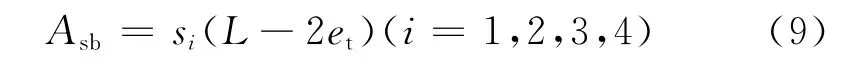
式中：Asb为星孔燃面面积，m2；i=1，2，3，4，对应4个燃烧阶段。

将Stt=πD2／4-Ap代入上式即得端面燃烧面积计算公式

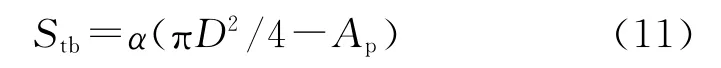
则总燃烧面积：

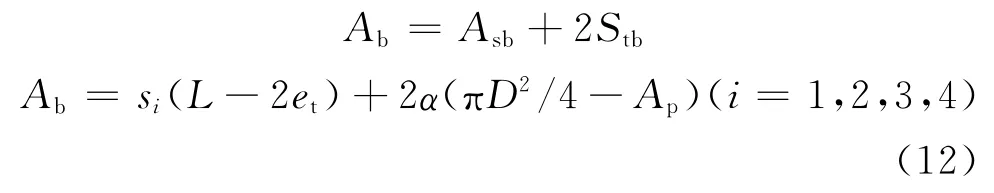
式中：Ab为总燃面面积，m2。

2 结果与分析

在相同的室温条件下完成9 发火箭发动机的装配，放入保温箱保温。试验分常温、低温和高温试验3组，每组试验3发，取3次试验数据的平均值作为每组的试验结果。采用零维火箭内弹道计算方法［5］，利用计算机采用四阶龙哥库塔法编程求解火箭内弹道方程。考虑到固体火箭发动机在工作时可能出现两种端部初始燃面恒定的极端工作状态：（1）药柱端面不参与燃烧，端部初始燃面面积为零；（2）药柱端面在发动机工作开始时刻全面瞬时点燃。所以计算时采用3 种燃面计算方法：（1）星孔全面瞬时点燃，上端面、下端面不参与燃烧；（2）星孔、上端面、下端面全面瞬时点燃参与燃烧；（3）星孔全面瞬时点燃、上端面、下端面逐渐点燃参与燃烧。

火箭装药为某双基型推进剂，药柱密度ρp=1.612g／cm3，火药力f=929 000J／kg，燃气绝热指数k=1.225，不同温度条件下的a、n值见表1。

表1 不同温度条件下的a、n值Table 1 The value of aand nat different temperatures

2.1 常 温

试验温度为+15℃，药柱初始温度为288.15K，α采用公式（2）计算。表2为火箭发动机性能特征量的试验值和计算值，得到的燃烧室头部p-t曲线见图2。

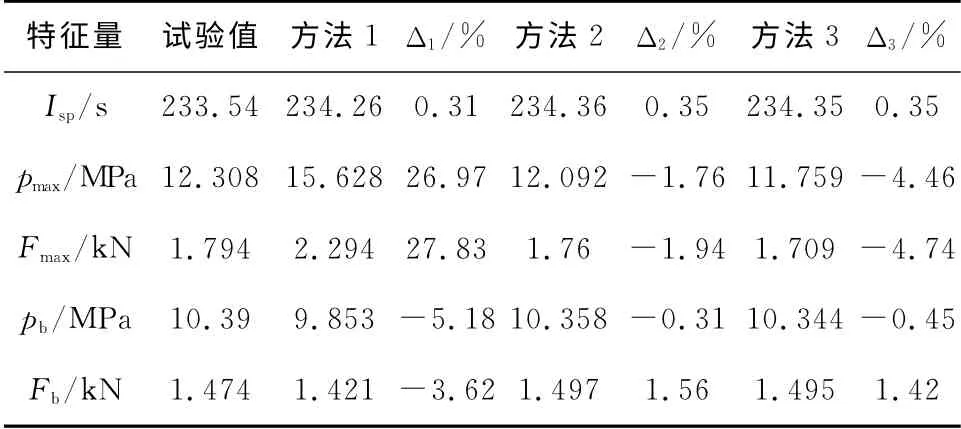
表2 +15℃时发动机特征量的试验值与计算值Table 2 Experimental and calculated results at of characteristic values of motor+15℃

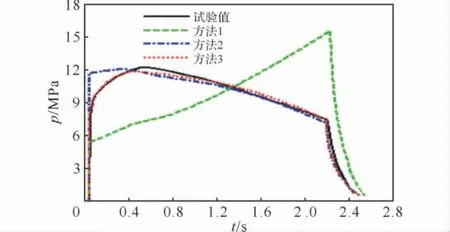
图2 +15℃时燃烧室头部的p-t曲线Fig.2 The p-t curves of chamber head at+15℃

从表2可以看出，方法1在最大压强和最大推力方面的相对误差分别高达26.97%和27.83%，理论值与试验值相差甚远；而方法2和方法3计算出的各项特征量相对误差均小于5%。

试验测试数据处理时剔除了试验测试曲线的初始压强峰。从图2可以看出，方法1计算得出的p-t曲线与试验明显不符，原因是燃烧过程中只有星孔参与燃烧，星孔的初始燃面面积小，导致初始阶段压强较试验值小，随着星孔燃面面积不断增大，压强也逐渐增大，压强呈上升趋势，与实际情况不符；方法2计算得出的p-t曲线在药柱初始燃烧阶段明显高于试验测试曲线，原因是方法2采用的是星孔和两端面瞬间全部点燃，初始燃面面积较大，致使初始阶段燃烧压力较高；方法3计算得到的p-t曲线仅在0.5～1.0s时间内稍低于试验测试曲线，其余部分与试验曲线基本吻合，特别是初始燃烧阶段吻合较好。

2.2 低 温

试验温度为+15℃，药柱初始温度T为233.15K，α采用公式（2）计算。火箭发动机性能特征量试验值和计算值见表3，发动机燃烧室头部p-t曲线，见图3。

从表3可以看出，方法1在最大压强和最大推力方面的相对误差分别高达27.53%和28.66%，误差较大；而方法2和方法3计算出的各项特征量相对误差均小于5%。

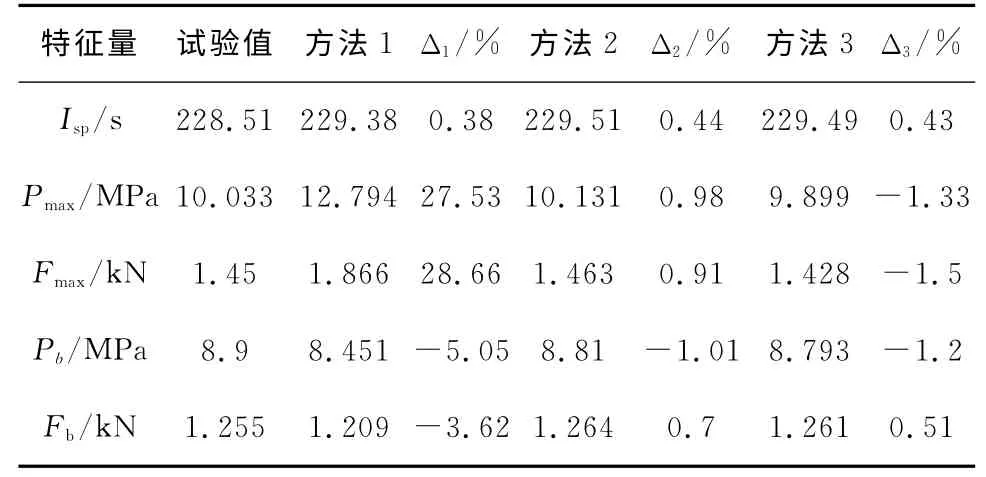
表3 -40℃时发动机特征量的试验值与计算值Table 3 Experimental and calculated results of characteristic values of motor at-40℃

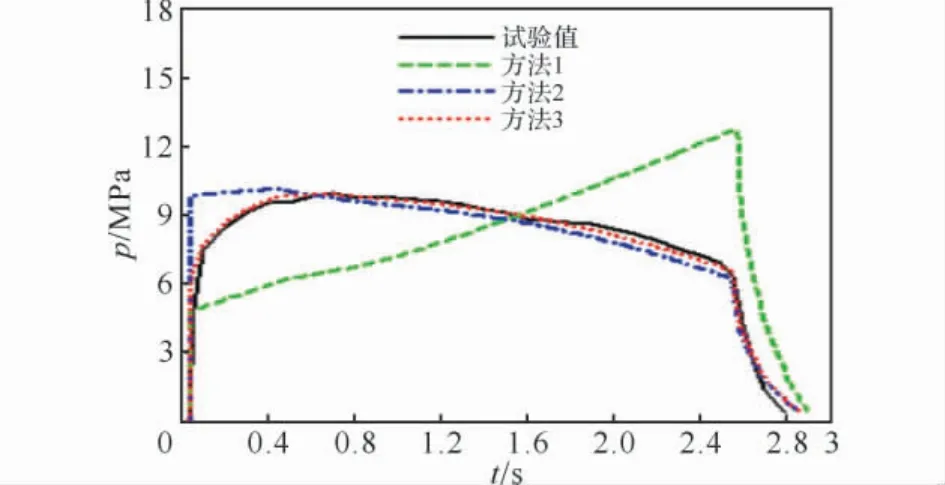
图3 -40℃时燃烧室头部的p-t曲线Fig.3 The p-t curves of chamber head at-40℃

图3中，用方法1计算出的p-t曲线与试验曲线明显不符；用方法2计算出的p-t曲线在药柱初始燃烧阶段明显高于试验测试曲线，而在后期又明显低于试验测试曲线；用方法3计算出的p-t曲线在整个燃烧过程中与试验曲线吻合较好，计算曲线和试验曲线均比较平滑。

2.3 高 温

试验温度为+50℃，药柱初始温度T为328.15K，α采用公式（3）计算，根据试验结果，取t0为0.5s。火箭发动机性能特征量试验测试和理论计算结果见表4，发动机燃烧室头部的p-t曲线见图4。

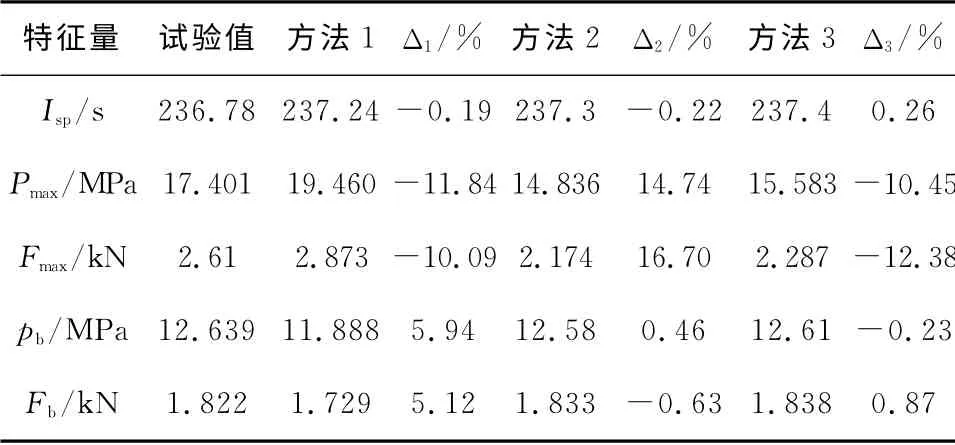
表4 +50℃下试验测试与理论计算结果Table 4 The experimental test and calculated results of characteristic value of motor at+50℃

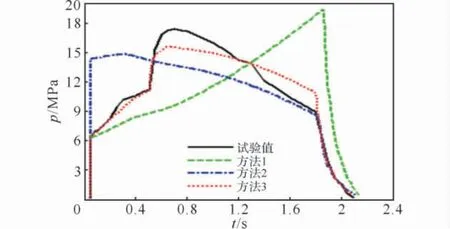
图4 +50℃时燃烧室头部的p-t曲线Fig.4 The p-t curves of chamber head at+50℃

从表4和图4可以看出，用方法1和方法2计算出的p-t曲线与试验曲线相差甚远，无法对火箭发动机性能进行有效预示，用方法3计算出的曲线在初始阶段与试验吻合较好，但在0.5s以后的曲线上升段和后期吻合不够理想。在常温下将火箭药柱装入发动机药室，令药柱的一端无约束，在+50℃条件下保温48h后，药柱沿轴向伸长0.58mm，火箭药柱在高温状态下受热膨胀，致使药柱端面与垫片间的间隙变小或消失，导致在初始燃烧阶段药柱端面正常参与燃烧，p-t曲线在初始阶段上升缓慢；但随着燃烧进行到大约0.5s，燃烧室压力升高到11MPa左右时，高温燃气开始急剧窜入药柱端面和垫片之间的间隙，点燃尚未参加燃烧的端面部分，总燃面面积突然增大，致使燃烧室压强陡然升高。

药柱在高温条件下受热膨胀伸长量若过大，严重时可使药柱端面、垫片和发动机壁面三者处于受压状态，间隙消失，使药柱端面不能正常燃烧，同时又使药柱内部产生应力，过大的应力又可诱发药柱表面或内部产生裂纹，甚至发生破碎，导致火箭发动机工作异常。燃烧室压强阶跃式升高很可能会破坏火箭发动机的结构，应避免此种情况的发生［6］。在火箭发动机装配时，药柱和垫片在轴向方向上要保留适当的间隙或加入间隙调节装置，以保证火箭发动机在高温条件下正常工作。

此外，在常温、低温和高温下，用方法3计算的药柱燃烧质量均为1.444kg，与药柱实际质量1.445kg接近，相对误差仅为-0.07%。

3 结 论

（1）在常温和低温条件下，星孔装药端面是以逐渐参与燃烧的方式进行燃烧，试验中可得到较为平滑的p-t曲线；而装药端面不参与燃烧和装药端面瞬时全面参与燃烧的方式与实际情况不符。

（2）通过引入端面燃烧参与度和端面等效燃烧厚度的方法，并结合试验条件推导出燃面面积经验计算公式，解决了药柱在燃烧过程中的燃面计算问题。在常温和低温条件下，计算值与试验值的相对误差均小于5%，计算得到的p-t曲线与试验曲线基本吻合；高温条件下稍显不足。

（3）采用上、下端面均无包覆星孔装药的火箭发动机工作稳定性受温度影响较大。药柱端面和垫片之间要留有适当的间隙或加入间隙调节装置，间隙大小可根据火箭发动机的具体药型尺寸和试验测试结果调整。

（4）端面燃烧参与度和端面等效燃烧厚度的引入提供了一种解决端部初始燃面可变的星孔火箭装药燃面计算问题的方法，可为同类固体火箭发动机内弹道性能预测提供参考。

［1］侯林法，杨忠雄.复合固体火箭推进剂［M］.北京：中国宇航出版社，1994.

［2］夏志全.端面燃烧发动机研制中应注意的几个问题［J］.固体火箭技术，2000，23（2）：12-15.

XIA Zhi-quan.Several problems for end burning solid motor development［J］.Journal of Solid Rocket Technology，2000，23（2）：12-15.

［3］许鹏，梁景媛，梁国柱，等.固体火箭发动机装药端面燃烧燃速畸变现象分析［J］.火炸药学报，2006，29（5）：32-34.

XU Peng，LIANG Jing-yuan，LIANG Guo-zhu，et al.Preliminary analysis on cone burning of solid propellant in end-burning rocket motors［J］.Chinese Journal of Explosives and Propellants，2006，29（5）：32-34.

［4］周长省，鞠玉涛，朱福亚.火箭弹设计理论［M］.北京：北京理工大学出版社，2005.

［5］董师颜，张兆良.固体火箭发动机原理［M］.北京：北京理工大学出版社，1996.

［6］邢耀国，董可海，沈伟.固体火箭发动机使用工程［M］.北京：国防工业出版社，2010.