复合固体推进剂松弛模量的获取方法
2011-01-28许进升鞠玉涛
许进升,鞠玉涛,郑 健,韩 波
(南京理工大学机械工程学院,江苏 南京210094)
引 言
松弛模量是研究固体推进剂力学性能的重要前提,一般通过材料的应力松弛实验获得,但在实验数据的处理方面,传统的方法忽视了松弛实验的应变加载阶段[1-2],得到的初始松弛模量偏小,精确度较差。Zapas、Matti Malinen、Joonas Sorvari[3-7]等人针对该问题进行了深入的研究,利用数值方法改进了松弛模量的获取方法,提高了其精确度。但此方法在数据处理方面需要计算应力的变化速率,对数据采集系统提出较高的要求,且数据处理比较繁琐。
本研究从线黏弹性理论出发,将松弛模量以Prony级数形式表示,结合松弛实验中测得的应力响应,拟合得到推进剂松弛模量中的材料参数。利用线性黏弹性理论计算哑铃型试件松弛实验和等速率拉伸实验过程中的应力响应,用该方法获取的松弛模量不仅精确度较高,且数据处理方便。
1 理论计算
本研究由线性黏弹性理论出发,其具体形式[8]:

式中:松弛模量E(t)以6 阶的Prony 级数形式表示,如式(2):

应力松弛实验中理想的应变加载过程如图1(a)所示,但拉伸实验机不可能获得理想的ε0阶跃载荷。实际松弛实验是将试件以等应变率拉伸或压缩t1时间后,达到恒应变值,并保持该应变值ε0一段时间,实时记录材料的应力响应,实际应变加载过程如图1(b)所示。

图1 松弛实验的应变过程Fig.1 Strain history in the relaxation test
1.1 传统方法
在获取材料松弛模量的传统方法中,忽略了应变的加载阶段,而将应变达到ε0的时刻t1作为松弛实验的初始时刻,则松弛模量可表示为:
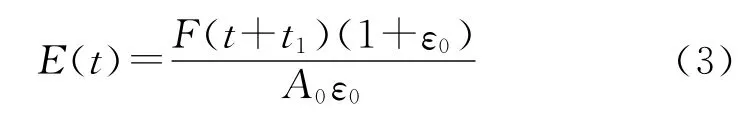
式中:E(t)为t时刻对应的松弛模量,MPa;F(t)为t时刻传感器测得的力,N;A0为材料试件的初始截面积,mm2;ε0为松弛应变水平。
该方法目前应用最为广泛,但由于在应变加载过程中,应力已经发生了一定的松弛,因此通过该方法获得的初始弹性模量比真实值要小。适用于松弛特性较弱的材料,但对于松弛特性较强的材料而言,会产生较大的误差,因此需要经过一定的处理,考虑等应变率加载阶段对应力松弛的影响。
1.2 Joonas方法
实际的应变加载过程可通过式(4)表述为:
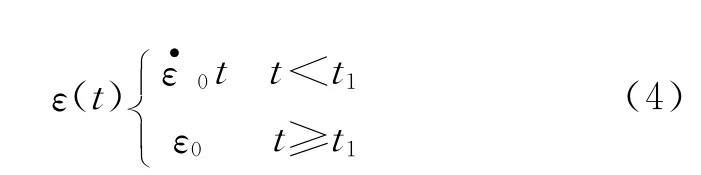
将实际的应变加载过程代入线黏弹性本构方程中得到:

将(6)式对时间进行求导得:

Sorvari和Malinen在2006年提出用梯形法则来近似求解(6)式:

(7)式、(8)式联合便可以得到:

或

式中:h为时间步长,该步长由松弛实验的数据采集频率确定。根据(10)式便可以通过t1时刻的应力值σ(t1)得到材料的初始松弛模量E(0)。式(11)中采用了数值近似计算的方式,为减小该近似造成的误差,需要提高数据采集系统的测试频率,减小时间步长h,对采集系统提出了较高的要求,且由于数据量大,对数据处理也带来了不便。
1.3 基于Prony级数的数据拟合法
本研究提出一种基于Prony级数的数据拟合法。该方法从线黏弹性理论出发,松弛模量以6阶Prony级数的形式表示。将实际的应变加载过程代入线黏弹性本构方程中得到:
当t<t1时,
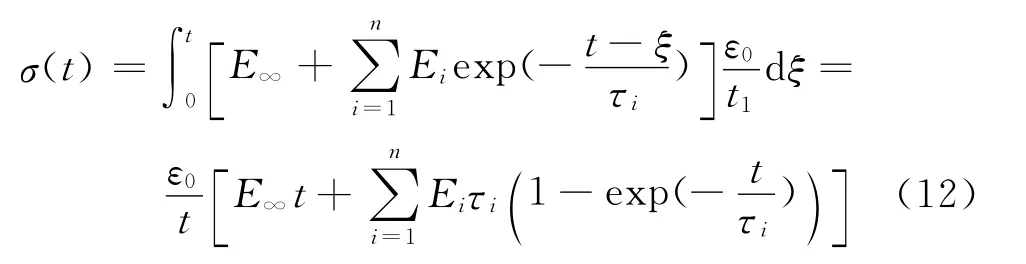
当t>t1时,
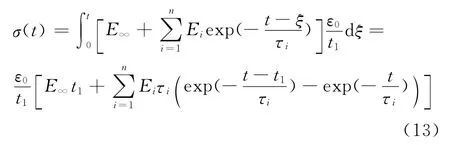
松弛实验中,可以方便地得到t>t1时试件中的应力响应σ(t)、应变ε0和时刻t1,利用以上数据,可以直接拟合得到松弛模量中的参数E∞、Ei和τi,可见该方法在处理数据方面较方便。
2 实验及数据处理
本研究针对HTPB 复合推进剂进行了应力松弛实验和等速率拉伸破坏实验,利用松弛实验测得的应力响应等数据通过上述3种方法进行处理,分别拟合出松弛模量中的材料参数。利用所得的松弛模量分别计算出松弛实验和等速率拉伸实验应力响应的理论解,并与松弛实验和等速率拉伸实验测得的应力响应实验值对比,以验证3种方法处理松弛模量的适用性和精确度。
2.1 松弛及等速率拉伸实验
采用QJ-211B型电子万能实验机,实验中保持恒温20℃,湿度70%。试件采用HTPB 复合固体推进剂板条形哑铃试件,尺寸如图2所示。

图2 试件尺寸示意图Fig.2 Schematic diagram of specimen size
松弛实验中应变加载过程为:加载速度为100mm/min,实际加载应变率为0.009 7s-1,加载时间t1=4.74s,应变水平为ε0=4.59%,松弛时间为1 800s,重复5次,实验数据取平均值。图3(a)为松弛实验获得的σ-t曲线。
为便于得到实验的理论解,可进行等速率拉伸破坏试验,拉伸速率为100mm/min,实际应变率为0.009 5s-1,重复5次,应力应变响应取平均值。图3(b)为等速率拉伸实验获得的σ-t曲线。
2.2 松弛模量的计算
数据处理过程中,传统方法和Joonas方法首先需要得到材料不同时刻的松弛模量,然后再将松弛模量拟合为6阶的Prony级数形式。而本研究提出的方法中,可直接根据式(13)拟合出松弛模量。3种方法得到的松弛模量如表1所示。
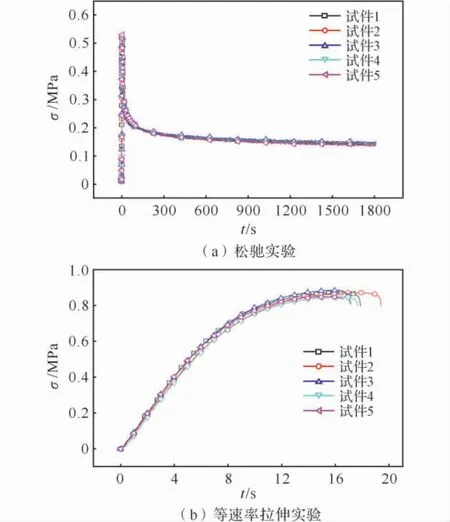
图3 实验获得的σ-t曲线Fig.3 σ-t curves obtained by experiments
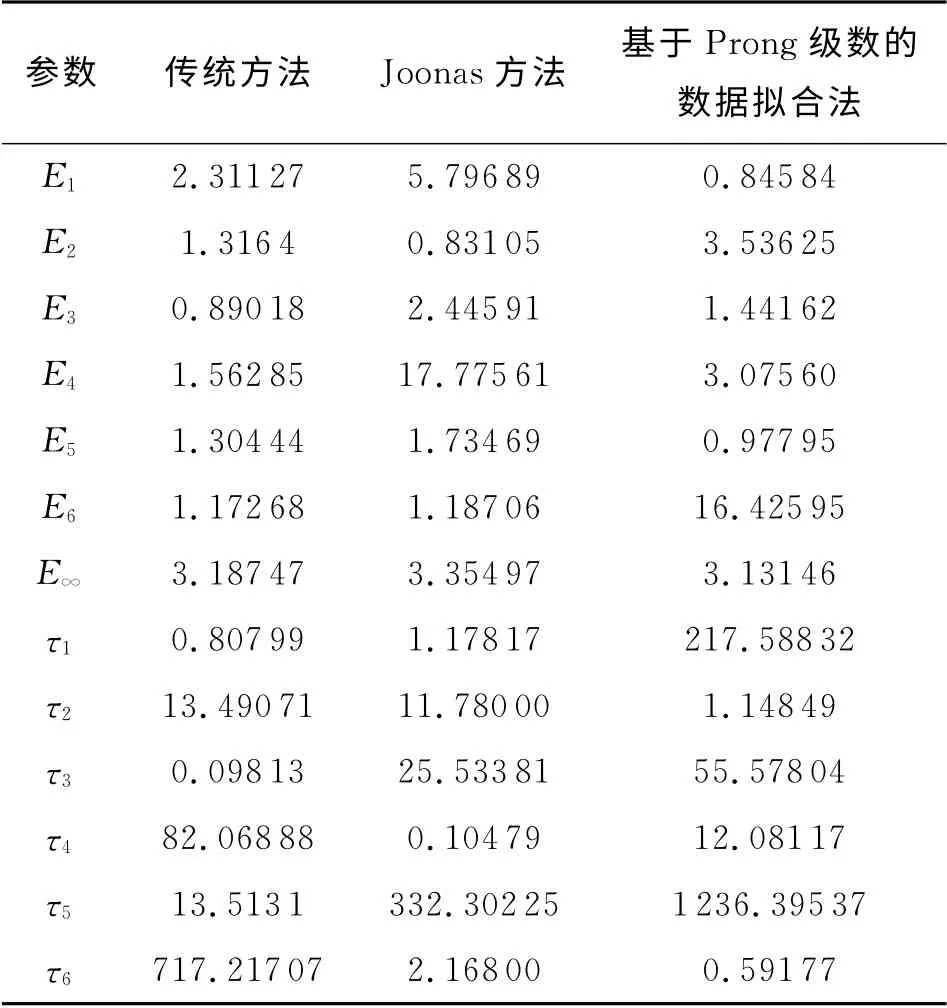
表1 Prony级数参数值Table 1 Values of Prony series coefficients
图4为3种拟合手段得到的松弛模量的对比,传统方法得到的初始松弛模量E0=11.745 28MPa,Joonas 方法拟合得到的初始松弛模量E0=33.126 19MPa,基于Prony级数的数据拟合法得到的初始松弛模量E0=29.434 67MPa。从图4中可以看到,三者的主要差别发生在前2s内,而随着时间的推移,三者之间逐渐趋于一致。且在前2s内,松弛模量的变化也最剧烈,说明该型固体推进剂的松弛现象较强,而在松弛实验中应变加载时间达到4.74s,因此不能忽视此阶段的应力松弛,这也是传统方法中初始松弛模量较其他两种小很多的原因。
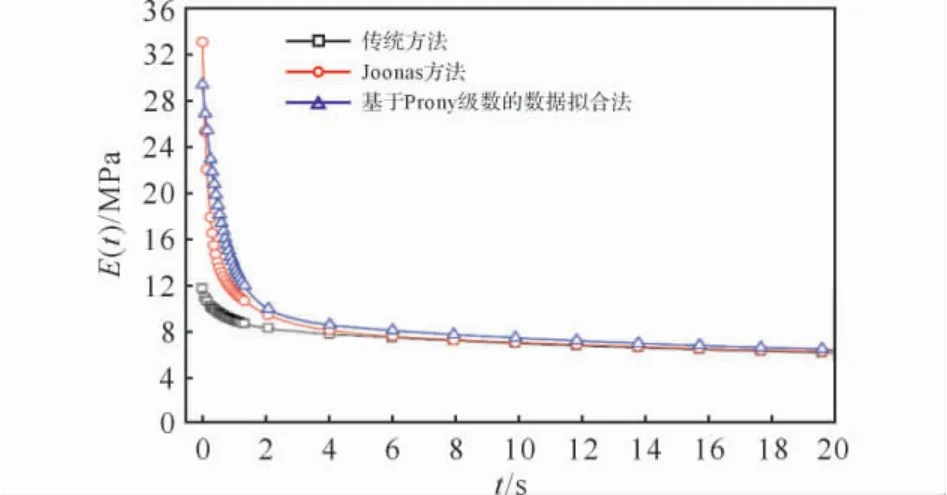
图4 3种方法拟合得到的松弛模量曲线Fig.4 Relaxation modulus curves obtained by the three ways
2.3 松弛模量的验证
利用上述3种方法拟合得到的松弛模量,计算应力松弛实验和等速率拉伸实验的应力响应理论解,通过与松弛实验和等速率拉伸实验的实验结果对比,以验证这3种方法处理松弛模量的适用性和精确度。
将所求的松弛模量分别带入(13)式,计算松弛实验中t1时刻以后的应力响应,并与实验结果进行对比,结果如图5所示。可以看到,实验数据比较符合Joonas方法和基于Prony级数的数据拟合法计算得到的曲线分布,且t1时刻的实验值与基于Prony级数的数据拟合法更渐近,而传统方法得到的曲线相对偏小。

图5 t1时刻后松弛应力实验结果与理论值的对比Fig.5 Comparison of the calculated values and experimental ones for relaxation after t1time
为进一步验证松弛模量的准确性,对材料在同等条件下进行了100mm/min拉伸破坏实验。图6为拉伸实验的应力—应变曲线实验值与理论值的对比。由图6可以看到,通过传统方法获得的理论值与实验值存在较大的差距,精确度较差;在材料的线性阶段,Joonas方法与基于Prony级数的数据拟合法与实验结果重合得较好,但由于材料在大变形下表现出明显的非线性特性,当应变值大于15%以后,理论值与实验结果发生了较大的偏差。因此可认为当该推进剂材料的应变小于15%时,线黏弹性理论仍有较好的适用性,当应变超出该范围时,应采用非线性黏弹性理论来描述材料的力学性能。实验结果表明,在计算黏弹性材料的松弛模量中,Joonas方法和基于Prony 级数的数据拟合法是很好的选择。
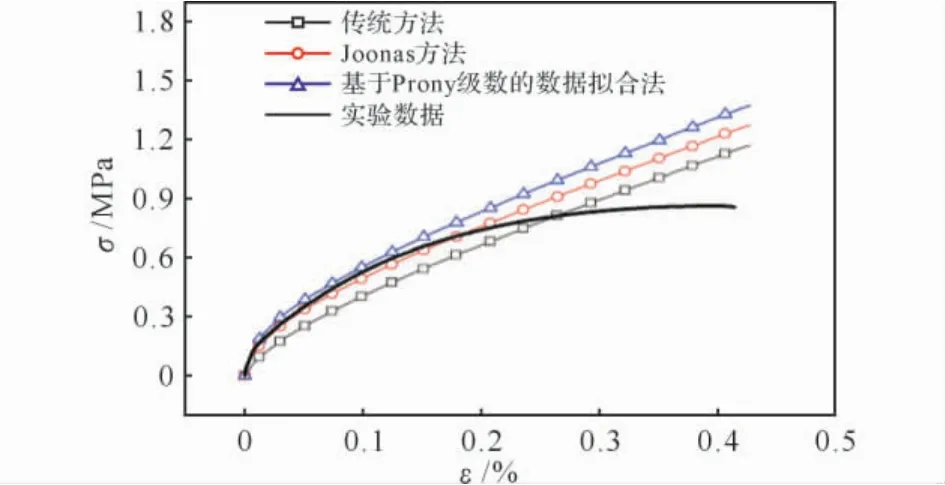
图6 等速率拉伸σ-ε实验结果与模拟结果对比Fig.6 Comparison of the experimental values by extension test at the constant rate and the calculated ones
3 结 论
(1)传统方法由于忽视了应变加载阶段的应力松弛,获得的松弛模量值在6s之前偏小,而6s之后与另外两种基本重合,适用于松弛特性较弱的材料。
(2)采用Joonas方法和基于Prony级数的数据拟合法均可得到较高精度的松弛模量。且对于第二种方法数据处理更方便,是计算黏弹性材料松弛模量较好的选择。
(3)用3种方法获得松弛模量的主要误差出现在前2s内,随时间的推移,三者逐渐趋于重合,且在前2s内松弛模量变化最剧烈,说明该推进剂的松弛现象较明显。
(4)对于HTPB 复合固体推进剂,当应变值小于15%,可采用简单的线黏弹性理论描述其力学性能;当应变值大于15%,需要采用较复杂的非线性黏弹性本构模型。
[1]胡全星,姜豫东,李健.推进剂松弛模量主曲线及WLF方程参数的拟合处理[J].固体火箭技术,2003,26(2):46-48.
HU Quan-xing,JIANG Yu-dong,LI Jian.Fitting of relaxation modulus master curve for solid propellant and WLF equation parameters[J].Journal of Solid Rocket Technology,2003,26(2):46-48.
[2]常新龙,余堰峰,张有宏,等.基于有限元理论的HTPB推进剂I型裂纹J积分数值模拟[J].火炸药学报,2010,33(5):60-64.
CHANG Xin-long,YU Yan-feng,ZHANG You-hong,et al.Simulation research on J integral of HTPB propellant with mode crack based on finite element theory[J].Chinese Journal of Explosives and Propellants,2010,33(5):60-64.
[3]QJ 2487-1993.复合固体推进剂单向拉伸应力松弛模量及主曲线测定方法[S].1993.
QJ 2487-1993.The way for determine the relaxation modulus and master curves of composite solid propellant by uniaxial tensile[S].1993.
[4]Sorvari J,Malinen M.On the direct estimation of creep and relaxation functions[J].Mechanics of Time-dependent Materials,2007(11):143-157.
[5]Sorvari J,Malinen M.Numerical interconversion between linear viscoelastic material function with regularization[J].Solids and Structures,2007 (44):1291-1303.
[6]Zapas L J,Philips J C.Simple shearing flows in polyisobutylene solutions[J].J Res Nat Bur Stds,1971,75A(1):3-41.
[7]Lee S,Knauss W G.A note on the determination of the relaxation and creep data from ramp tests[J].Mechanics of Time-dependent Materials,2000(4):1-7.
[8]Flory A,Mckenna G B.Finite step rate corrections in stress relaxation experiments:A comparison of two methods[J].Mechanics of Time-dependent Materials,2004(8):17-37.
[9]Findly W N,Lai J S,Onaram K.Creep and relaxation of nonlinear viscoelastic materials with an introduction to linear viscoelascticity[M].New York:[s.n.],1989.
