大口径超短身管高低压发射装置内弹道过程的数值模拟与试验研究
2011-01-28杨正才吴玉均
杨正才,廖 昕,江 坤,吴玉均
(1.南京理工大学化工学院,江苏 南京210094;2.南京理工大学动力工程学院,江苏 南京210094;3.北方特种能源集团有限公司庆化分公司,陕西 西安710025)
引 言
大口径超短身管发射装置常用于发射直径较大、炮口初速和膛压较低的弹丸。因此,其发射装药较少,药室容积相对较大,且由于身管口径较大,发射过程中药室容积增大速率较大。这些因素对于火药的点火一致性、燃烧稳定性和炮口初速的稳定性都是非常不利的。对于短管炮装药及内弹道问题,陆中兵采用两相流模型进行了研究[1],计算结果与实验结果吻合较好。为了改善超短身管发射装置的内弹道性能,可应用高低压火炮的发射原理对发射装药结构进行重新设计[2-3]。其优点是可以得到更为稳定的内弹道参数。陶如意等人将高低压发射技术应用于平衡炮的发射和子母弹抛撒中,取得了较好的效果[4-5]。国内外学者对高低压点传火内弹道数值模拟进行过一些有益的探索和研究[6-8]。这些研究工作对高低压发射技术的研究起到了良好的推动作用。本研究在前人工作的基础上,对大口径超短身管发射装置内弹道过程进行了数值计算和试验研究,以期能为该类研究的设计提供参考。
1 实 验
1.1 材料与仪器
3号黑火药与2/1樟火药由四川泸州化工厂生产。
601H 型压电式压力传感器,瑞士Kistler公司;DW2500型瞬态信号记录仪,奥地利Dewetron公司。
1.2 试验方案
为了验证内弹道计算代码的准确性和所设计方案的可行性,在某150mm 口径超短身管发射装置上进行试验研究。在低压药室管壁开测压孔,安装压力传感器,获得不同装药方案下压力—时间曲线。在炮口前方安装测速网靶,对炮口初速进行了测试,采用高速录像系统记录弹丸的发射过程。
根据发射装置的工作情况,分正常装药、强装药和减装药3种工况对超短身管发射装置的发射过程进行数值模拟和试验研究,3种工况下主装药均为3号黑火药与2/1樟火药的混合装药,在不同工况下黑火药质量均为10g,2/1樟火药药量不同。
2 内弹道模型
2.1 内弹道过程基本假设
超短身管发射装置的内弹道过程包括点燃点火药、点火药引燃主装药、药粒和燃气的流动、燃气膨胀做功、弹丸的运动等多种物理化学现象。采用集总参数法和空间平均的热力学参数来描述火药的燃烧和弹丸的运动。基本假设如下:
火药燃烧模型:火药的燃烧满足几何燃烧定律、燃速定律的条件,其中燃速定律为平均压力的指数函数;点火药瞬间燃完,并形成主装药的点火压力。主装药仅在高压室内燃烧,并不随火药气体流入低压室。
火药燃气模型:燃气服从诺贝尔方程,组分冻结;燃气流动为等熵流动。在高压室和低压室中火药燃气分别均匀分布。
弹丸运动模型:燃烧室内压力达到启动压力后,弹丸瞬间解除约束并开始运动;且弹丸的运动为轴向一维运动,所受运动阻力用虚拟质量系数进行考虑。
热散失、弹丸运动摩擦功等各种形式的次要功用次要功计算系数进行修正。
2.2 内弹道过程的划分
根据药室和弹丸的状态不同将内弹道过程分为3个阶段:
(1)第一时期:火药点火燃烧至高压室内达到破膜压力。该时期点火药瞬间燃完并均匀分布于高压室,此后火药仅在高压室做定容燃烧,在该时期弹丸行程为0,低压室内压力也为0(相对于大气压力)。
(2)第二时期:从高压室喷口破膜开始,至低压室压力达到弹丸启动压力。该过程为低压室定容充气过程,当低压室内压力达到弹丸启动压力时弹丸开始运动,内弹道过程进入第三时期。
(3)第三时期:从弹丸启动开始至弹丸出膛口。该时期模型包含火药燃烧、火药气体流动、弹丸运动等现象。
2.3 内弹道数学模型
2.3.1 火药燃烧方程
火药燃烧满足指数燃烧定律:

火药形状函数:

式中:Zi为火药已燃相对厚度;e1i为火药初始弧厚的一半;u1i为燃速系数;ni为燃速指数;p为高压室平均压力;Ψi为火药已燃质量百分比;χi、λi、μi均为火药形状特征量;χis和λis为火药分裂点后形状特征量;Zik为分裂后碎粒全部燃完时的燃去相对厚度;下标i为第i种火药。
2.3.2 高压室气体状态方程
依据阿贝尔-诺贝尔方程给出高压室气体状态方程:
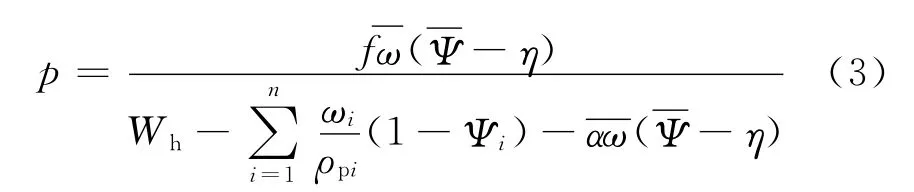
式中:Wh为高压室容积;η为高压室气体相对流出量;f与则由下式确定:
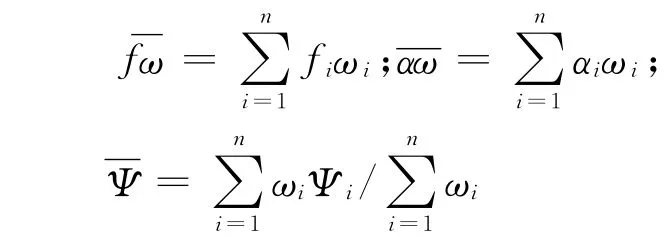
式中:fi为火药力;ωi为装药质量;αi为火药余容。该混合装药计算式中含完全燃完的依据点火药。
2.3.3 低压室的能量守恒方程
内弹道学基本方程给出低压室的能量守恒方程:
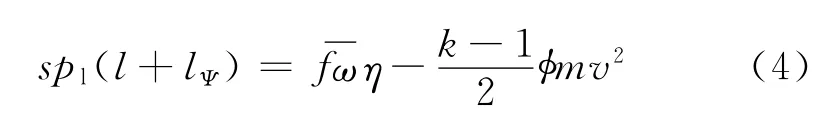
弹丸启动前速度v=0,行程l=0。
式中:pl为低压室的平均压力;η为火药气体相对流量;l为弹丸运动距离;lΨ为低压室初始自由容积缩径长,即:
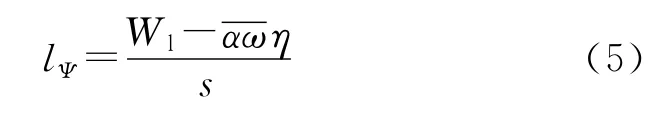
式中:Wl为低压室初始容积。
2.3.4 火药气体流量方程
根据假设,气体由高压室流入低压室为等熵流动,则气体流量公式可由下式给出;
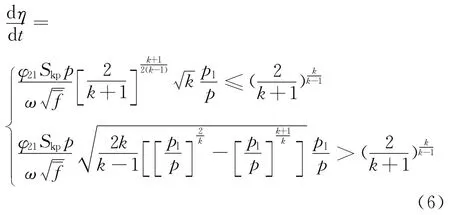
式中:SKP为高压室喷口面积;φ21为消耗系数;pl为低压室平均压力;ω为装药总质量;f-为等效火药力,由下式确定:
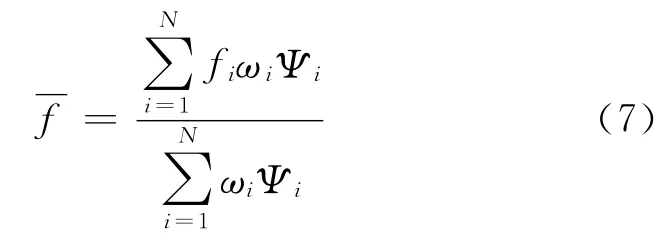
弹丸运动方程:
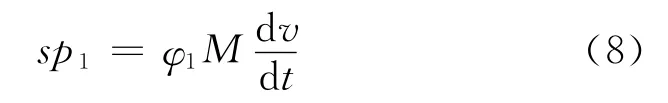
式中:M为弹丸质量;v为弹丸速度;φ1为弹丸质量系数。
根据以上模型方程,采用四阶龙格-库塔法编制了内弹道程序,并根据技术指标进行装药选择和内弹道计算。
3 结果与分析
根据试验设计所制定的内容,分别进行了数值计算和试验验证。各工况下的内弹道计算和试验结果如表1所示。
3.1 3种装药条件下低压室压力计算曲线与试验曲线的对比
图1给出3种情况下低压室压力计算曲线和试验曲线的对比。正常装药下试验重复进行3发,其余工况进行1发。由图1可见,计算压力曲线与试验压力曲线较为接近。计算所得内弹道过程持续时间较试验值小,其中一个比较重要的原因是内弹道模拟中假设弹带瞬间挤进,而实际弹带挤进过程需要一定的时间。另外由于所选用弹丸为平头弹,弹丸出炮口后速度会迅速下降,且试验所测初速点位于炮口前方0.5m左右,因此所测得炮口初速会略小于计算值。
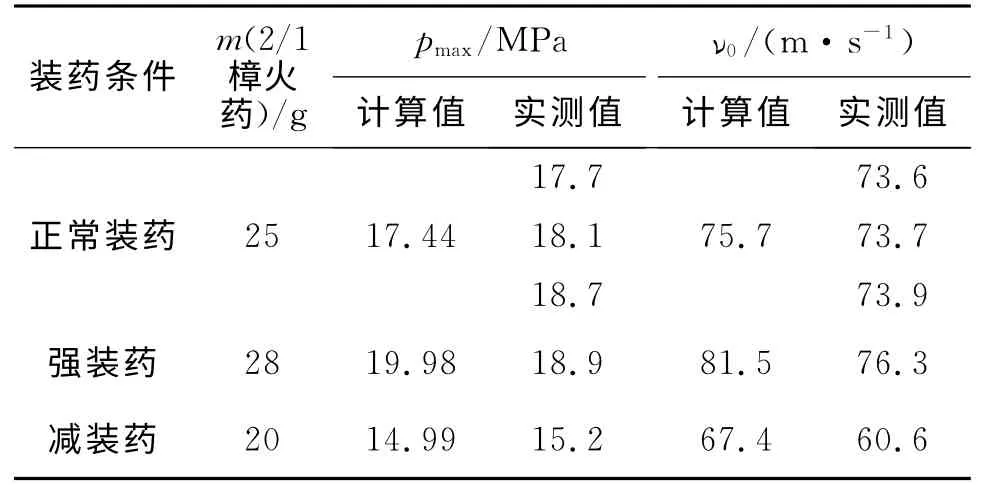
表1 各工况下的计算与试验结果Table 1 Computational results and experimental ones under different charge conditions
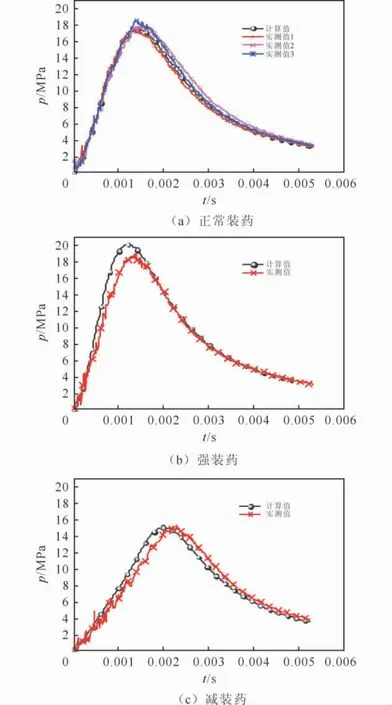
图1 不同装药条件下低压室压力-时间曲线Fig.1 The p-t curves of low pressure chamber under different charge conditions
3.2 3种装药条件下高压室与低压室计算压力的对比
图2给出了各工况下计算所得高压室和低压室压力—时间曲线。由于身管非常短,弹丸出炮口时火药均未燃烧完全,图中高压室压力一直大于低压室压力。随点火药瞬间燃完并引燃主装药,高压室压力迅速上升;达到高压室破膜压力后气流开始按流量公式第一式(公式(6)),即以声速向低压室流动;此后高压室压力上升开始逐渐变缓,直至高压室压力开始下降;而此过程中低压室压力一直处于上升状态,当时,流量开始按亚音速向低压室流动,此时高压室压力降低速度开始变缓,直至高压室压力又重新开始升高;当低压室压力上升至弹丸启动压力时弹丸开始加速运动,此时由于弹丸运动速度较低,低压室容积膨胀不是很大,其压力不会迅速降低,同样高压室压力也仍然处于上升阶段;当弹丸速度达到一定值后低压室压力开始下降,高压室压力也开始下降;此后随弹丸速度的增加两室压力迅速下降,直至弹丸出炮口。由于以上原因,所得高压室压力成双峰值形状。但并不是对于所有高低压发射过程,高压室压力都呈双峰值形状。随火药装填量的增加,高压室第一个峰值的大小明显增大,并在强装药情况下其第一个压力峰值大于第二个压力峰值。高压室出现两峰值情况不仅与喷口流动状态有关,也与高压室装填密度有关。对于较低装填密度情况,可能仅在切换流量公式时,即气流在喷孔流速由音速变为亚音速时刻附近压力曲线产生的拐点,即存在压力变化速率的改变。

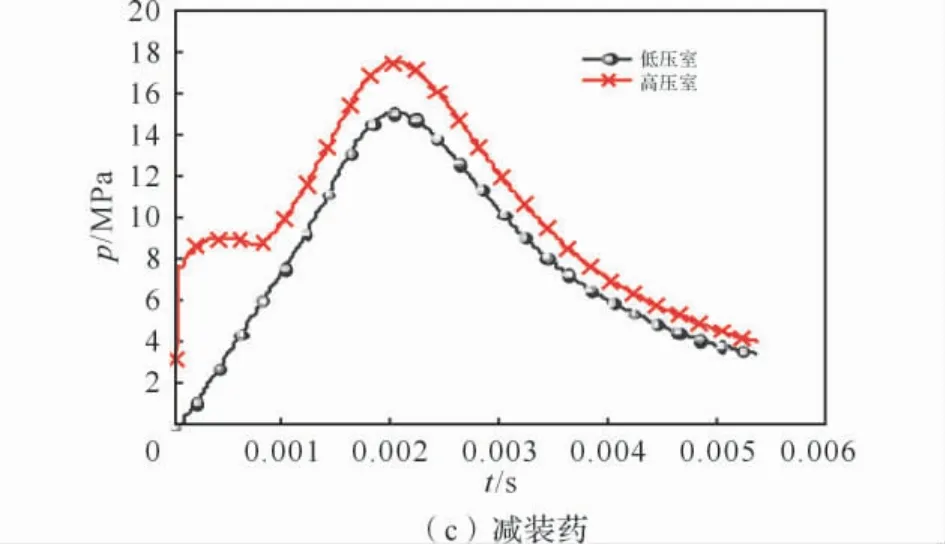
图2 不同装药条件下高压室和低压室的压力-时间曲线Fig.2 The p-t curves of high and low pressure chamber under different charge conditions
4 结 论
(1)所得计算结果与试验结果较为一致,可以满足工程应用的要求。
(2)高压室压力-时间曲线成双峰值形状,峰值大小与喷口形状及高压室火药装填密度有关。高压室与低压室压差先增大再减小,又增大再减小,直至压差趋于0。
(3)对于大口径超短身管发射装置内弹道计算,如需得到较为精确的计算结果,需要采用内弹道两相流模型对高低压药室内燃烧及流动规律进行深入研究。
[1]陆中兵,周彦煌,王育维.短管炮模块装药两相流内弹道模拟[J].南京理工大学学报,1999,23(2):105-108.
LU Zhong-bing,ZHOU Yan-huang,WANG Yu-wei.Two phase flow interior ballistic simulation of the short-barrel gun with modular charges[J].Jorunal of Nanjing University of Science and Technology,1999,23(2):105-108.
[2]金志明.枪炮内弹道学[M].北京:北京理工大学出版社,2004.
[3]翁春生,王浩.计算内弹道学[M].北京:国防工业出版社,2006.
[4]陶如意,孙继兵,黄明,等.高低压室平衡炮内弹道数值模拟及试验研究[J].南京理工大学学报.2006,30(4):478-485.
TAO Ru-yi,SUN Ji-bing,HUANG Ming,et al.Interior ballistics simulation and experimental study of low and high pressure chamber Davis gun[J].Journal of Nanjing University of Science and Technology,2006,30(4):478-485.
[5]黄蓓,王浩,陶如意.带导向管的子母弹活塞式抛撒弹道建模及数值仿真[J].兵工学报,2009,30(12):1584-1590.
HUANG Bei,WANG Hao,TAO Ru-yi.Ballistic modeling and numerical simulation of cluster bomb with piston dispensing and guiding tube[J].Acta Armamentarii,2009,30(12):1584-1590.
[6]Legeret G,Taiana E,Boisson D.Study of the ignition of a large caliber modular charge,computation and validation[C]//Proceeding of 17th International Symposium on Ballistics.Midrans:The South African Ballistics Organization,1998.40-44.
[7]张永强,郭炳彦,韩继娟.高低压室发射系统内弹道数值模拟[J].光电技术应用,2008:23(2):75-78.
ZHANG Yong-qiang,GUO Bing-yan,HAN Ji-juan.Numerical simulation on the interior ballistics of highlow pressure chamber launcher[J].Electro-optic Technology Application,2008,23(2):75-78.
[8]潘玉竹,余永刚.点火管气固两相流模拟喷射装置的设计与计算[J].火炮发射与控制学报,2010(2):88-91.
PAN Yu-zhu,YU Yong-gang.Design and calculation of simulating injection device for gas-solid two-phase flow in igniter tube[J].Journal of Gun Launch and Control,2010(2):88-91.
