磁共振成像中数据空间与k空间转化的推导及讨论*①

侯淑莲 王广新 赵强 谢寰彤 李石玉

(河北联合大学 河北 唐山 063000)

磁共振成像(Magnetic Resonance Imaging，简称 MRI)与X-CT、超声、SPECT等成像的最大不同是没有外在的放射源，产生的信号强度没有与坐标的直接对应关系.MRI利用处于磁场中具有磁矩的氢原子核受到射频脉冲的激励后，在接收线圈中产生感生电信号；通过一系列的物理手段使信号既带有生物组织信息又带有坐标(位置)信息，然后采集这些信号.用射频脉冲激发，这涉及到射频脉冲的类型、幅度、宽度、施加的时刻、持续的时间.如果把成像断层分成体素，各体素产生的信号强度依赖于体素内自旋核密度及环境，采集这些信号还原自旋核密度的空间分布就是实现图像重建.为了使信号中带有坐标信息，目前通用的方法是通过施加梯度磁场用频率去标示这些体素的坐标.这就涉及到梯度磁场施加的方向、时刻、顺序、持续的时间等.其次是信号的采集，是直接采集FID信号还是采集回波，是梯度回波还是自旋回波，在哪一时刻采集，用什么方式采集，要采集反映生物组织哪一方面特征的信息，如何加快采集速度提高信噪比等等.出现了各种各样的参数和各种各样的脉冲序列,使得磁共振成像原理变得异常复杂和难以理解.为了更方便地处理以上问题，使采集到的时间域信号更快地实现模 - 数转换，更好地利用在频率域处理信号简单、快捷的优势,通过傅里叶变换实现图像重建引入“k空间”的概念.实际是用计算机存储数据的一个方法.由于它不是一个物理空间,而与成像的物理空间又有非常密切的关系,所以对于初学者来说，k空间既是一个很难理解的概念，又是一个很重要的空间.它是为傅里叶变换图像重建提供数据、提供重要图像解释方式的基础.有了它，不必采用复杂的数学演算就可以进行脉冲序列的信号强度、组织对比、优势、缺陷以及对应的伪像、分辨率、信噪比的讨论.它也是MRI仪器制造过程中的关键技术之一.

现行教科书中,k空间的引入大多数仅限于定性讨论，很难深入理解;有的推导虽然注意了科学性与严密性，但又太高深，使数理基础不太深厚的医学专业的学生理解起来有困难.现尝试用普通物理学的方法引入k空间，并对其实质给予进一步的分析.

1 一维傅里叶变换图像重建与k空间的引入

傅里叶变换及逆变换如下

(1)

(2)

时域信号与频域信号可通过傅里叶变换相互转化，MRI中坐标是用频率与相位表示的，所以傅里叶变换图像重建是MRI的最佳选择.图1给出了傅里叶变换图像重建用频率表示空间位置的原理.

图1

(3)

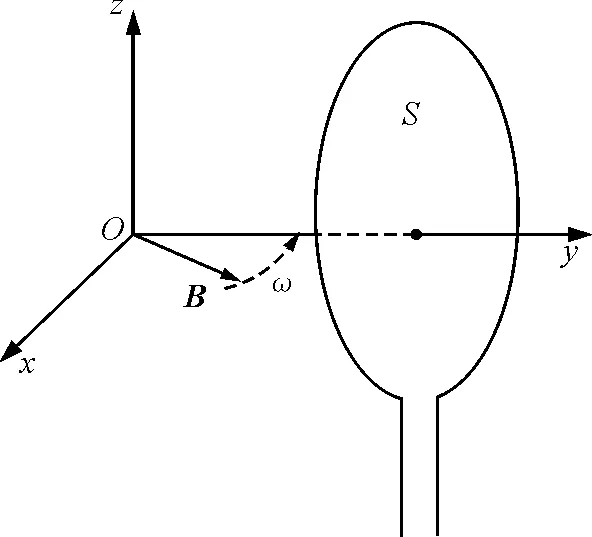
图2 旋转磁场在静止线圈中产生感生电动势

由此出发考查一个自旋核一维分布的样本.设体素沿x方向，自旋核密度为ρ(x)，设主磁场B0方向为z方向.由于氢核自旋对于外磁场的取向作用使氢核的基态能级发生分裂，使样本中每一个体素产生沿主磁场方向的磁矩dMz，整个样本沿主磁场产生的总磁矩为M0，如图3(a).设沿x方向施加90°射频(RF)脉冲，则各dMz或M0一方面绕主磁场

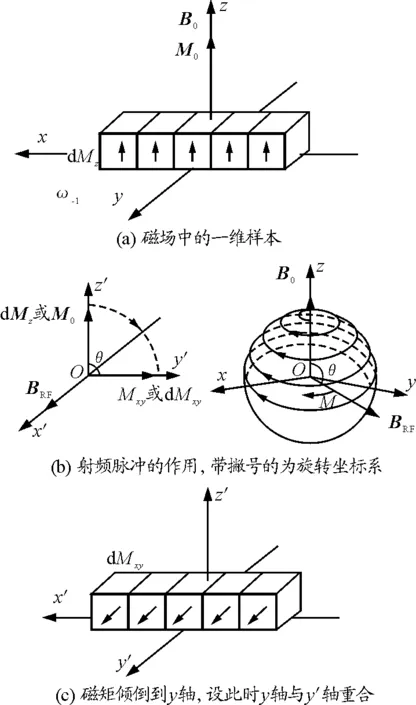
图3 磁共振信号的产生

B0旋进，另一方面绕射频磁场BRF旋进，如图3(b)，总效果是旋转着倒向xOy平面(可设倒向y轴)，一般忽略弛豫衰减有dMxy=dM0，各体素磁矩同相位，如图3(c).此后RF结束横向磁化强度矢量失去射频脉冲的束缚，自由地在xOy平面旋进，由于局部磁场的差异很快散相即所谓弛豫，产生信号，如图3(d).为了建立信号的坐标，90°RF后加线性梯度场Gx进行频率编码，如图3(e).频率编码的同时，采集时域信号，并把此信号转化为用k表示的频域信号数据，存贮到计算机的一个空间叫做k空间填充，后面有专门的介绍，见图3(f).设90°RF结束时，t=0，各体素有相同的初相位，且φ0=0，并假设主磁场均匀，不存在横向分量，则由

ω=γB[3]

(4)

倾倒后的横向磁化强度矢量dMxy进动频率为

ω=ω0+Δω=ω0+γGxx

(5)

用频率标记坐标.设接收线圈法线沿y轴，将dMxy用复数表示将更方便[3]

dMxy= (dMy+idMx)e-t/T2=

dM0(cosωt+isinωt)e-t/T2=

dM0eiωte-t/T2

(6)

其中e-t/T2为横向弛豫(衰减)项，t=TE时采集信号.当TE≪T2时，可忽略弛豫衰减(也可归入等效自旋密度之中)，所以有dMxy=dM0eiωt.由式(3)可知，信号(感生电动势)的强度与旋转角频率ω成正比，与磁感应强度成正比;在本问题中也就是与磁化强度矢量dM0成正比，而dM0∝自旋核密度ρ(x)，每个体素产生的信号

dε∝ρ(x)ω(x)eiωtdx

信号的强度还与弛豫时间、温度、电子线路、场及其他一些复杂因素有关，但自旋核密度是最基本的成像参数，不存在自旋核的地方不会有信号，其他因素依赖于自旋核密度，把上式写为等式

dε=Λρ(x)ω(x)eiωtdx

为了研究方便,引入有效自旋密度概念.于是令ρ(x)=Λωxρ作为有效自旋密度，其中Λ为比例系数，包括了影响信号的一些因素，采集到的信号

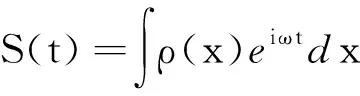
(7)

积分范围是自旋核密度不为零的区域.为了旋进的稳定性，射频脉冲是一个旋转磁场，其角频率与dMz绕着主磁场旋进的角频率相同为ω0.建立旋转坐标系，与实验室坐标系z轴相同.若以旋转坐标系为参考系(相当于信号解调)，由

ω=ω0+Δω=ω0+γGx·x

则在旋转坐标系中,dMxy旋转的角速度为Δω=γxGx.把相位用角度表示，式(7)变为

(8)

负号表示横向矢量旋进角速度方向与确定相位角(逆时针为正)的方向相反.令kx=γGx·t,量纲为Hz·cm-1,称做空间频率，表示沿空间某一方向单位距离内波动的周期数，是一个矢量，又称为波数.这样就把时间t隐含到空间频率之中，式(8)可写为

(9)

显然，(9)式恰恰是等效自旋核密度ρ(x)的傅里叶变换式.通过线性变换把用时域信号S(t)表示的采集信号转化为用频域信号S(kx)表示出来，把信号与自旋密度联系起来.从傅里叶的逆变换则很容易得到自旋核的密度分布，重建图像

(10)

由以上研究可见，用k标记的信号就是有效自旋核密度沿线性梯度方向的傅里叶变换，变换的变量是空间频率k，随时间和梯度强度变化.所以一维空间成像通过频率编码用频率记录空间位置的信息，用这些以频率表示的数据组成新的结构——k空间.具体形成过程如下：设一维样本含有Nx个体素，每次采集到的信号是所有体素信号的和，从数学原理上来说，需有Nx次采集才能解出各体素的信号强度(或密度).在施加频率编码持续时间t2内,在t=τ,2τ,3τ,…以等间隔时间τ连续采集Nx次，形成Nx个以k表示的数据点，组成一行，形成一维的一个数据空间，由于用k作变量就称为k空间，相邻点间的频率差为Δω=γGxΔx.显然以一定顺序储存数据S(k)的空间就是k空间.以上是从理论上对傅里叶变换、k空间的物理意义而作的简化推导,浅显易懂.在MRI实际制造中，直接把接收到的时域信号S(t)通过傅里叶变换化为频域函数

(11)

进行傅里叶空间填充，然后作傅里叶逆变换实现图像重建，式(11)与式(9)是等价的.

2 二维傅里叶变换及k空间的形成

对于二维样本假设由Nx×Ny个体素构成.要想使每一个体素都具有用频率表示的坐标，除了在x方向施加线性梯度场Gx频率编码外，还要在y方向施加相位编码线性梯度场Gy，使二维断面上的体素再获得用频率表征的纵坐标.具体过程是RF脉冲后核磁矩倒向y轴，首先，施加相位编码梯度场持续时间t1,结束时不同y坐标的体素获得不同的相位，接着施加频率编码梯度场同时采集时间域信号S(t1,t2)，转化成用kx，ky表示的一行数据，形成k空间的一行，将式(8)应用到二维

S(kx,ky)=∬dxdyρ(x,y)e-i2π(kxx+kyy)

(12)

其中

ky=γGy·t1kx=γGx·t2

(13)

积分范围遍及自旋核存在的区域.与一维一样，式(12)是等效自旋核密度ρ(x)的傅里叶变换式，所以对(12)式进行二维傅里叶逆变换即得到有效自旋密度分布函数，实现图像重建

ρ(x,y)=∬S(kx,ky)ei2π(kxx+kyy)dkxdky

(14)

与一维情况一样，S(kx,ky)可通过采集的时域函数S(t1,t2)的二维傅里叶变换得到

S(kx,ky)=∬S(t1,t2)e-2πi(kxx+kyy)dxdy

(15)

对Nx×Ny体素平面，需要采集到Nx×Ny个信号;所以相位编码需进行Ny次.现在加相位编码梯度场的方法是由负向最大等间隔增加到正向最大，一次相位编码对应一次频率编码采集Nx个信号对应k空间的一行，Gy=0对应k空间中央行.相位编码进行Ny次后，填满Ny行，组成Nx×Ny的二维k空间.最终图像重建信号经傅里叶逆变换实现，一般经计算机软件处理来完成.二维傅里叶变换结果一般用复数表示，其实部作为幅度频谱表示强度或灰度，虚部为相位频谱表示坐标.

3 关于k空间

(1)k空间与成像物理空间

k空间每一个数据点都是断层上所有体素贡献的.虽然二维空间是由二维数据点构成，但并不与物理空间直接对应.k空间内的频率编码轴不直接对应最终图像的频率编码轴，频率编码轴的左右两极并不对应MR图像的左侧和右侧部分，而是对应此轴线上图像的细节.但k空间与真实成像平面物理空间是有关系的,若以Δωmax表示成像物体两端对应的最大频率差有

Δωmax=γGxNxΔx=γGxFOVx

(16)

上式中，视野(Field of View,FOV)FOVx=NxΔx.设k空间一行中相邻点间频率差为Δω，可见要得到同样Δω，增加磁场梯度即可减小Δx，就是提高了分辨力，增加采集次数可增大视野.相位编码方向与x方向类似.又由频率与周期的倒数关系可得到同一行中相邻点之间点距Δkx

(17)

(2)k空间数据在图像重建中的作用

在ky=0的中央行，MR信号是在Gy=0时获得的，不存在相位编码梯度磁场产生的散相，信号的幅度也就最大；随着Gy正负方向的增加，相位编码梯度磁场引起的散相也开始增加，信号的幅度也就降低了.在x方向也是如此.kx=0时采集的信号正好是每个回波的中心，因而幅度最大；而在k空间的周围列，MR信号采集时则是回波的旁边部分.总之，越靠近k空间边缘，信号越弱.所以k空间中心部分对应的MR信号幅度大，主要形成图像的对比度.由k空间中的行距Δky和同一行Δkx及Δωx=γGxΔx,Δωy=γΔyGy表明，对于同样的空间两点间的距离Δx或Δy梯度场越大,对应的频率差别越大,则两点分得越开，分辨率越好.所以对k空间的外围部分虽然信号幅度低,但能很好的分辨细节，用来产生图像的分辨率.通过k空间分析磁共振成像已成为最方便最重要的手段.所以k空间是MRI研究中非常重要的空间.

参考文献

1 E.Mark Haacke,Robert W.Brown,et al著.曾晓庄，包尚联译.核磁共振成像物理原理和脉冲序列设计. 北京：中国医药科技出版社,2007

2 赵凯华,陈熙谋.电磁学. 北京：高等教育出版社,1985

3 俎栋林.核磁共振成像学. 北京：高等教育出版社,2004