〈l,t〉几何凸函数及应用研究

蒋志萍,李世杰

(1.浙江外国语学院理工学院,浙江杭州310012;2.浙江省衢州市教育局教研室,浙江衢州324002)

1 引 言

凸函数是一个重要的数学概念,在数学基础理论研究中它所发挥的作用是无可替代的[1-2].类比凸函数的概念,文献[3]中提出如下的几何凸函数概念:

设f(x)在区间M(⊆R+)上有定义,如果对于任意的x1,x2∈M和t∈[0,1],都有

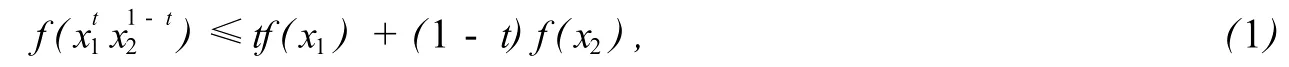
则说f(x)在M上是几何凸函数,如果(1)中不等号反向,则说f(x)在M上是几何凹函数.

文献[4]作了更广泛的研究,从中可以看出几何凸函数在不等式研究中具有重要的作用.文献[5]提出〈l,t〉凸函数概念:

设f(x)是定义在实线性空间X中的凸集D上的实值连续函数,若对∀x1,x2∈M(⊆D),λ∈[0,1]和给定的常数l,t,都有λx1+(1-λ)x2+l∈D,且f[λx1+(1-λ)x2+l]+t≤λf(x1)+(1-λ)f(x2),则称f(x)为M上的〈l,t〉凸函数.并对〈l,t〉凸函数及其应用作了初步的研究,这启发我们可以对几何凸函数作类似的推广研究.本文下面提出更一般的m维空间的〈l,t〉几何凸函数概念.

2 〈l,t〉几何凸函数的定义

为方便计,引入下列记号:M=M1×M2×…×Mm(Mi为[ai,bi],或(ai,bi),或无穷区间,i=1,2,…,m,m≥1).若Mi=R+=[0,+),i=1,2,…,m,则M记作Rm+.

下面给出〈l,t〉几何凸函数的定义:

定义 设M是m个区间的笛卡尔积,f(X)是定义在M(⊆Rm+)上连续的数值函数,t是常数,l为正常数,若对任意的

则称f(X)是M上的〈l,t〉几何凸函数;如果上面不等式的不等号反向,则称f(X)是M上的〈l,t〉几何凹函数.

值得指出的是,〈l,t〉几何凸函数含有两个参变数l,t,与它不同的几何凸函数定义有:

(1)吴光耀在文[6]中提出的L-几何凸函数的关系式:

中只含有一个参变数L,是〈l,t〉几何凸函数当l=1,t=0时的推广.

(2)在专著[7]中,张小明采用的几何凸函数定义,是〈l,t〉几何凸函数当→f(x)时的特殊情况(该定义由本文作者之一李世杰提出).

3 关于〈l,t〉几何凸函数的不等式

定理1 设f(X)是M上的〈l,t〉几何凸函数,即对任意的X1,X2∈M,λ∈[0,1],t是常数,l为正

则对任意的

其中p表示满足2p-1＜n≤2p的整数.

如果l+t=1,(2)中等式成立的条件是X1=X2,则(3)中等式成立的条件是X1=X2=…=Xn.

下面用反向数学归纳法来证明这一结论.

证明 当l+t=1时,首先证明n=2p(p∈N,p≥2)时结论成立.

当n=2时,由(2)及其等号成立的条件知结论成立.

假设n=2k(k∈N,k≥2)时,结论成立,即对∀Xi∈M(i=1,2,…,k),有

等式成立的条件是X1=X2=…=X2k.则对Xi∈M(i=2k+1,2k+2,…,2k+1),有

等式成立的条件是X2k+1=X2k+2=…=X2k+1.

又根据n=2时的结论,在(2)中作置换

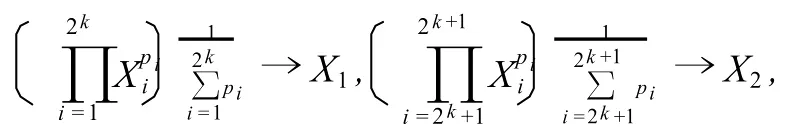
得

等式成立的条件是

故由上面方程组可推得(7)中等式成立的条件是X1=X2=…=X2k+1.

因此对n=2k+1(k∈N)结论也成立.可见,对n=2p(p∈N,p≥2)结论恒成立.

当2p-1＜n＜2p时,令pn+1=pn+2=…=p2p→0,由n=2p时的(3)式得

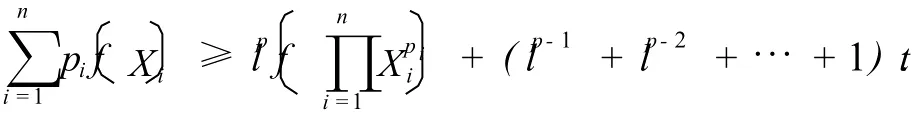
综上,就证明了不等式(3)结论对n≥2恒成立.

当l+t≠1时,若X1=X2,(2)中等号不成立,但由不等式(2)仍可推出不等式(3)成立,证明过程完全类似,略.

注 当l=1,t=0,f(X)=x时,定理1给出的是加权的算术——几何平均值不等式.

推论1 设g(X)(X∈M)是正值函数,若对任意的X1、X2∈M,λ∈[0,1],t,l是正常数,都有

其中p表示满足2p-1＜n≤2p的整数.

证明 在定理1中令f(X)=lng(X),lnt→t,(2)、(3)变形即得(8)、(9).

推论2 (乘积型函数不等式)设g(X)是定义在M上的正值函数,t,l＞0,,若对任意的X1、X2∈

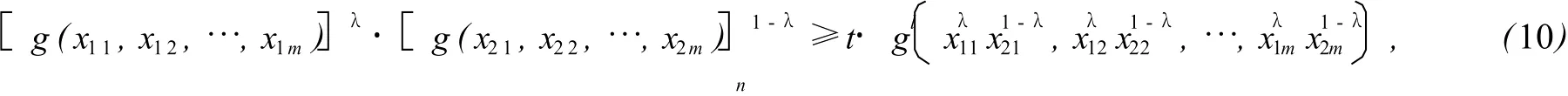
其中p表示满足2p-1＜n≤2p的整数.

证明 在定理1中令f(X)=lng(X),lnt→t,即可得证.

命题1 (算术型函数不等式)设正值函数f(X)的定义域为λ∈[0,1],t,l＞0,若对任意的X1、X2∈都有

其中p表示满足2p-1＜n≤2p的整数.

证明 在定理1中令f(x)=g(lnx),exi→xi,即可证明.

命题2 (方幂型函数不等式)设非负函数f(X)的定义域为,αi≠0,i=1,2,…,m,λ∈[0,1],r,t,l＞0,若对任意的X1、X2∈,都有

其中p表示满足2p-1＜n≤2p的整数.

4 应 用

〈l,t〉几何凸函数的的应用是十分广泛的,上面我们得到的一系列不等式,是我们常见的一些著名不等式的共同来源.

如定理1,取m=l=1,t=0,可得丹麦数学家琴生(Jensen,1859-1925)1905年证明的著名的琴生不等式;如命题2的结果也是多姿多彩的,取m=r==l=1,t=0,则

①当α1=-1时,可得调和型函数不等式;

②当α1=k(k∈N,k≥1)时,可得乘方型函数不等式;

限于篇幅,其它结果不再一一列出.下面再举二个应用实例.

例1 设xi≥1,pi≥0(i=1,2,…,n,n≥2),

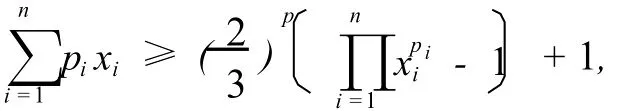
其中p是满足2p-1＜n≤2p的整数,等号当且仅当x1=x2=…=xn=1时成立.

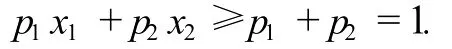
由琴生不等式,可得

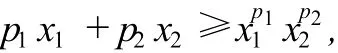
所以

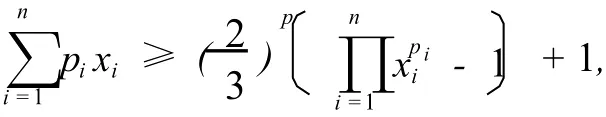
其中p是满足2p-1＜n≤2p的整数,等号当且仅当x1=x2=…=xn=1时成立.

例2 设0≤xi≤2,pi≥0(i=1,2,…,n,n≥2),

其中p是满足2p-1＜n≤2p的整数.

证明 当n=2时,对任意的由于λ∈[0,1],0≤xi≤2(i=1,2),我们有

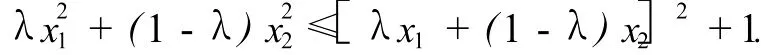
设f(x)=x2,x∈[0,2],上式即λf(x1)+(1-λ)f(x2)≤f[λx1+(1-λ)x2]+1,应用命题2,即可证得:

其中p是满足2p-1＜n≤2p的整数.

[1]Hardy G H,Little wood J E,Polya G.不等式[M].越民义,译.北京:科学出版社,1965:76-85.

[2]Mitrinovic D S,Vasic PM.分析不等式[M].赵汉宾,译.南宁:广西人民出版社,1986:13-27.

[3]李世杰.几何凸函数的若干性质[J].数学通讯,2003(5):37-40.

[4]吴善和.几何凸函数与琴生型不等式[J].数学的实践与认识,2004(2):155-163.

[5]李世杰,石焕南.〈l,t〉凸函数初探[J].北京联合大学学报,2005(3):19-24.

[6]吴光耀.关于L-几何凸函数的不等式初探[J].湖南理工学院学报:自然科学版,2010(1):13-16.

[7]张小明.几何凸函数[M].合肥:安徽大学出版社,2004:100-106.