具有8pq阶自同构群的有限幂零群
2011-01-25李春琴
孟 伟,李春琴
(云南民族大学数学与计算机科学学院,云南昆明650031)
讨论有限群G的结构一直是群论研究的一个热点,文献[1]研究了有限群中非正规子群的数量,文献[2]讨论了覆盖避开子群对有限群结构的影响.给定正整数n,确定有限群X,使得 |Aut(X)|=n,其中Aut(X)表示X的自同构群,也是一个很有意义的问题.Iyer[3]证明了至多有有限个 X满足上述方程.Machale和Flannery[4-5]给出了 |Aut(G)|=pn(1≤n≤4)及pq的有限群的构造,并证明了不存在自同构群阶是 p5,p6,p7的交换群(p为奇素数).Curran[6]得出结论:对任一奇素数 p,|Aut(X)|=pn(1≤n≤5) 无解,Flym[7]给出了 |Aut(X)|=25的全部解.陈贵云[8]研究了自同构群阶为无平方因子或pq2的有限群.Hegarty[9]给出了自同构群阶为p2q2的有限群分类.李世荣[10-11]完整解决了 |Aut(G)|=p3q的情形.杜妮和李世荣[12]解决了满足 |Aut(G)|=4pq情形的有限群G的分类.钟祥贵和李世荣[13]解决了 |Aut(G)|=2p2q的情形.孟伟等[14]给出了具有4p2q阶自同构群的幂零群的完全分类.作为以上问题的继续,本文研究具有8pq阶自同构群的有限群的结构,给出了满足条件的幂零群的完全分类.
所考虑的均为有限群,所有未经说明的记号和术语都是标准的.另外,Zn表示n阶循环群,Zp×Zp为p2阶初等交换群,Q8表示8阶四元数群,D8表示8阶二面体群.
1 预备引理
引理1[15]设P为非循环p-群,|P|>p2.若|P/Z(P)|≤p4,则
引理2[16]设n为整数且为n的素因子分解式,记 ω(n),则不存在有限群G,使得 |Aut(G)|为奇数且ω(|Aut(G)|)≤4.
引理3[17]设G为有限群.若 |Aut(G)|=2,则G≅Z3或Z4.
引理4[17]设G为有限群.若 |Aut(G)|=4,则G≅Z5或Z6.
引理 5[17]Aut(Q2)≅S4;Aut(D2)≅D4.
2 主要结果
定理1 设G是有限循环群.则|Aut(G)|=8pq(p,q为不同奇素数)当且仅当G是下列群之一:
i)Z8pq+1或 Z2(8pq+1)或 Z(8pq+1)2或 Z2(8pq+1)2;
ii)Z3(4pq+1)或 Z6(4pq+1)或Z4(4pq+1)或 Z3(4pq+1)2或 Z6(4pq+1)2或 Z4(4pq+1)2;
iii)Z5(2pq+1)或Z10(2pq+1)或Z8(2pq+1)或Z5(2pq+1)或Z10(2pq+1)2或Z8(2pq+12;
iv)Z12(2pq+1)或Z12(2pq+1)2;
v)Z3(2p+1)(2q+1)或Z6(2p+1)(2q+1)或Z4(2p+1)(2q+1)或Z36(2q+1);
vi)Z(4p+1)(2q+1)或Z2(4p+1)(2q+1)或Z25(2q+1)或Z50(2q+1)或Z225或Z450.
其中2p+1,2q+1,4p+1,2pq+1,4pq+1,8p+1,8pq+1皆为素数.
证明 G是循环群,因循环群可以分解成循环p群的直积,则有 G=P1×P2×…×Ps,其中Pi循环且为G的Sylow pi子群,而p1,p2,…,ps是整除|G|所有不同素因子.进一步可得|Aut(G)|=Aut(P1)×Aut(P2)×…×Aut(Ps),由假设知8pq=|Aut(G)|8pq.根据引理 2,按下表中6种情形讨论:
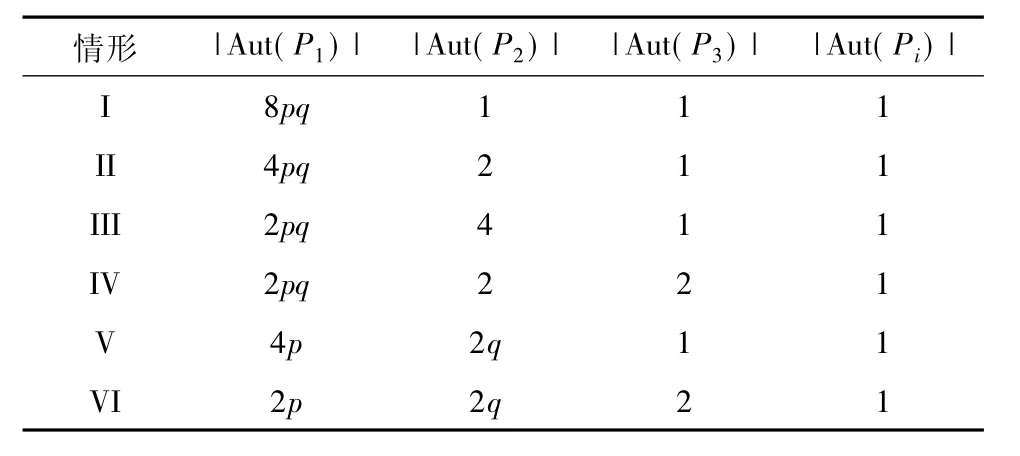
表1 Sylow子群自同构群的阶
检查表中的6种情形,根据引理3和引理4,只需讨论自同群阶满足如下5种情形的循环p群:
i) 若|Aut(Pi)|=8pq,即 pni-1i(pi-1)=8pq.
当pi=8pq+1时,即Pi≅Z8pq+1.当pi8p2q+1 时,若 pi=q=8p+1,则 ni=2,Pi≅Z(8pq+1)2.
ii) 若 |Aut(Pi)|=4pq,即 pni-1i(pi-1)=4pq .
当 pi=4pq+1 时,即 Pi≅Z4pq+1.当 pi≠4pq+1时,则pi=q=4p+1,则ni=2,即有Pi≅Z(4pq+1)2.
iii)若 |Aut(Pi)|=4q ,即 pni-1i(pi-1)=4q .
当 pi=4q+1 时,即Pi≅Z4q+1.当 pi4q+1时,则 pi=q=5,ni=2,即有 Pi≅Z25.
iv) 若|Aut(Pi)|=2pq,即 pni-1i(pi-1)=2pq .
当 pi=2pq+1 时,则 Pi≅Z(2pq+1).当 pi2pq+1 时,则 pi=q=2p+1,ni=2,即有 Pi≅Z(2p+1)2.v)若|Aut(Pi)|=2q ,即 pni-1i(pi-1)=2q.
当 pi=2q+1 时,则 Pi≅Z2q+1.当 pi≠2q+1 时,则 pi=q=3,ni=2,即有 Pi≅Z9.
再次根据G=P1×P2×…×Ps及引理3,4可得定理中6大类循环群,于是至此定理证毕.
定理2 设G是有限非循环的幂零群.则|Aut(G)|=8pq(p,q为不同奇素数)当且仅当G是下列群之一:
i)Z2×Z2×Z2;
ii)Z2×Z2×Z4q+1,其中4q+1为素数;
iii)Z2×Z2×Z52;
iv)Z2×Z2×Z2q+1×Z3,n其中2q+1为素数.
证明 因G是幂零群,则有G=P1×P2×…Ps,其中Pi为G的Sylow pi子群,而pi,p2,…,ps是整除|G|所有不同素因子.进一步可得Aut(G)=Aut(P1)×Aut(P2)×…Aut(Ps),由假设知8pq=|Aut(G)|=
因G非循环,所以必存在某个pi非循环,不失一般性可设P1非循环.若|P1|≥p31时,由引理1得此时必有 P1=2 且|P1|=8.因此,p1同构于 Z2×Z2×Z2,Z4×Z2,D8,Q8.易知 |Aut(Pi)|=23·3·7,8,8,24.根据引理2 可得 G=P1≅Z2×Z2×Z2.
若|P1|=且P1≅Zp1×Zp1.如果P1≥3,因为|Aut(P1)|=|GL(2,p1)|=p1(p1-1)(,于是得出,再一次矛盾.所以 P1≅Z2×Z2.此时 |Aut(P1)|=6.因此 |Aut(G)|=8·3q.
根据引理2可分如下情形:
i)|Aut(P2)|=4q;此时若 p2=4q+1,则 P2≅Z4q+1,得 G=P1×P2≅Z2×Z2×Z4q+1.若 p24q+1 ,则p2=q=5,n2=2,即 P2≅Z52,得 G=P1×P2≅Z2×Z2×Z52.
ii)|Aut(P2)|=2q;此时|Aut(P3)|=2,可得 P3≅Z3.若 p2=2q+1,则 P2≅Z2q+1,此时 G=P1×P2×P3≅Z2×Z2×Z2q+1×Z3.若 p22q+1,则p2=3,这与 p3=3矛盾.
至此定理证毕.
[1]孟伟,史江涛.有限群中非正规子群数量的一个标注[J].云南民族大学学报:自然科学版,2010,19(5):360-362.
[2]胡学瑞,李幸洋.覆盖避开性与幂零性[J].云南民族大学学报:自然科学版,2008,17(4):311-314.
[3] IYER H K.On solving the quation Aut(X)=G[J].Roky Mountain J Math,1979,9(4):653 -670.
[4] FLANNERY D,MACHALE D.Some finite groups which are rarely automorphismgroups- Ⅰ[J].Proc Royal Irish Acad,1981,81A(2):209 -215.
[5] MACHALE D.Some finite groups which are rarely automorphismgroups-Ⅱ[J].Proc Royal Irish Acad,1983,83A(2):189-196.
[6] CURRAN M J.Automorphisms of certain p-groups(p odd)[J].Bulletin of the Australian Mathematical Society,1988,38(2):299-305.
[7] FLYM J,MACHALE D.Determining all finite groups whose automorphismgroup is p - group[J].Proc Royal Irish Acad,1991,91A(2):259 -264.
[8]陈贵云.自同构群阶为p1p2…pn或 pq2的有限群[J].西南师范大学学报:自然科学版,1990,15(1):21-28.
[9] HEGARTY P V.Automorphismgroups of order p2q2[J].Proc Royal Irish Acad,1995,95A(2):149 -152.
[10] LI S R.Finite groups with automorphismgroup of order 23p[J].Proc Royal Irish Acad,1994,94A(2):193 -205.
[11] LI S R.Finite groups with automorphismgroup of order p3q(p odd)[J].Proc Royal Irish Acad,1994,94A(2):207 -218.
[12] DU Ni,LI S R.Finite groups with automorphismgroup of order 4pq[J].Acta Mathematica Sinica,2004,47:181 -188.
[13] ZHONG Xianggui,LI S R.Finite groups with automorphismgroup of order 2pq2(p>q>2) [J].Proc Royal Irish Acad,2006,106A(2):179 -190.
[14]孟伟,娄本功,卢家宽.具有4p2q阶自同构群的有限幂零群[J].云南大学学报:自然科学版,2009,31(s2):327-329.
[15] DAVITT R M.On the automorphismgroup of a finite p -group with a small central quotient[J].Canadian Journal of Mathematics,1980,32:1 168 -1 176.
[16] LI S R.Automorphismgroups of some finite groups[J].Science in China Ser A,1994,37(3):295 -303.
[17]徐明曜.有限群导引:上册[M].北京:科学出版社,1999.
