柴油机EGR温度的智能控制策略*

王惜慧 黄正展 赵荣超 黄旭为 刘玹

(华南理工大学机械与汽车工程学院，广东广州510640)

排气再循环(EGR)技术能有效降低柴油机NOx排放，EGR温度影响燃烧放热规律、燃烧温度以及缸内压力［1-2］.EGR温度与排气温度和EGR冷却系统密切相关，排气温度体现了排气热损失，影响燃烧效率、排放性能和排气温度传感器使用寿命［3］.柴油机运转时，排气温度变化大大滞后于柴油机运行工况变化，对EGR温度在线控制需要采用预测控制方法，预测控制的基础是建立柴油机排气温度模型，但是由于柴油机排气温度变化范围大［4］及受燃烧状况的影响，排气温度与柴油机运行工况呈非线性关系，因此建立适合柴油机各种运行工况的排气温度模型比较困难.

通过温度传感器测量柴油机不同工况下的排气温度，利用相应的辨识方法找到排气温度变化规律，可以建立排气温度模型.由于神经网络具有自学习、自组织和并行处理等特征，一些学者将其应用于系统辨识和模式识别中［5-7］.由于柴油机建模困难，所以神经网络以及模糊控制等智能控制技术已被应用于柴油机控制领域［8-9］.BP神经网络是应用广泛的基于BP算法的多层感知器，具有较为完善的数理基础和多功能性，随着其应用的扩大，目前出现了一些改进的BP神经网络结构.文中利用改进的BP神经网络算法，建立柴油机多工况下的排气温度模型，分析模型误差，并利用模型分析柴油机工况变化对排气温度的影响.以排气温度辨识模型为依据，根据模糊推理，设计EGR温度控制策略，为EGR温度的控制提供理论依据.

1 神经网络模型

神经网络模型虽然被冠以“黑箱”名称，但业内普通认为一个有意义的神经网络模型应该是输入、输出量之间具有内在规律性，且有一定物理意义;同时这些规律也是选择神经网络的依据.在柴油机排气温度辨识模型的建立过程中，首先需要找到影响排气温度的主要因素，然后确定适合的网络模型.

如果不计空气带入的能量，柴油机排气温度估算式为

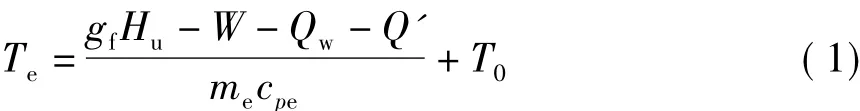
式中，Te为排气温度，gf为燃料量，Hu为燃料低热值，W为柴油机输出功，Qw为冷却水带走热量，Q'为润滑油带走的热损失，me为排气量，cpe为比定压热容，T0为环境温度.

方程(1)右边各项均影响排气温度，其中燃料量、做功量、冷却水带走的热量对排气温度影响较大，冷却水带走的热量又直接受柴油机转速和负荷影响，因此，选用燃料量、柴油机转速、柴油机负荷3个量作为排气温度的主导影响因素.

1.1 BP神经网络模型

理论和实践表明，三层BP神经网络可以以任意精度逼近一个连续函数，BP神经网络适合非线性系统辨识.文中采用3个输入、1个输出的三层BP网络(结构如图1所示)作为辨识模型.

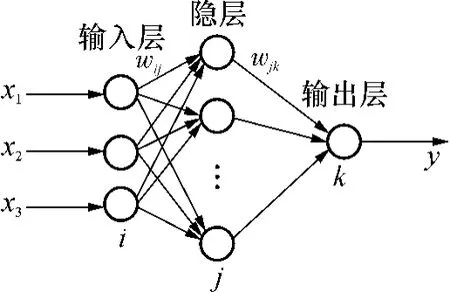
图1 三层BP神经网络的结构Fig.1 Structure of a 3-layer BP neural network

图1是一个3输入、单输出的三层BP网络，该网络只有一个隐层，因而可通过增加隐层神经元来提高模型精度.在此隐层选用8个神经元，隐层神经元作用函数f(x)选用双曲正切函数，输出层选用线性函数:

为了弥补标准BP算法收敛速度慢、有局部最小值的缺陷，在此利用动量法，通过引入动量因子α对权函数进行修正:

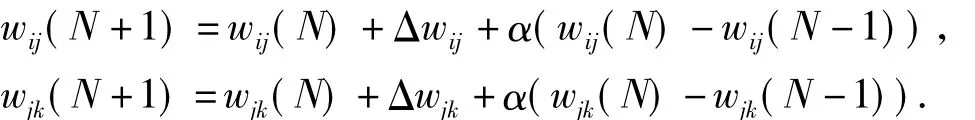
式中，N为计算的步数.

引入动量因子后，修正量与误差相关，在接近局部极小点时减少修正量，在误差较大时减小修正量，从而起到加速学习的作用.

1.2 实验样本数据整理

选用单缸DL190-12柴油发动机为样机(单缸，四冲程，标定功率为8.1kW(2200r/min)，缸径×行程为90mm×110 mm，压比为18)，利用柴油机台架测得不同工况下柴油机的排气温度(如表1所示).实验台架主要仪器为Y20型水力测功机、HT-3数字转数表、温度仪、天平、秒表.实验步骤如下:启动柴油机让柴油机处于稳定工作状态(转数表读数稳定);利用天平和秒表计算柴油机消耗10 g燃料所用的时间，并在发动机排气总管处测量柴油机平均排气温度;调整水力测功机让柴油机处于不同的负荷下，重复操作，记录柴油机在变负荷下的排气温度.

表1 单缸柴油机台架实验数据Table 1 Beach test data of single-cylinder diesel engine

为了合理利用实验数据训练神经网络模型，对表1中的实验数据进行标准化和归一化处理，处理后的数据如表2所示，表2中所有样本数据在0～1之间.以转速、负荷和油耗率为输入量，以排气温度为输出量，对1.1节所建神经网络模型进行训练，获得柴油机排气温度辨识模型.

表2 单缸柴油机样本数据Table 2 Sample data of single-cylinder diesel engine

2 辨识结果分析

对图1所示神经网络模型设置参数，取动量因子α为0.9，利用表2中数据对神经网络模型进行训练，获得辨识模型、训练误差和辨识结果，如图2－5所示.

由图2中可见，当训练次数达到80次时，模型误差接近0.001，并且不再进一步减小，即误差收敛，此时模型精度控制在0.01～0.001之间.

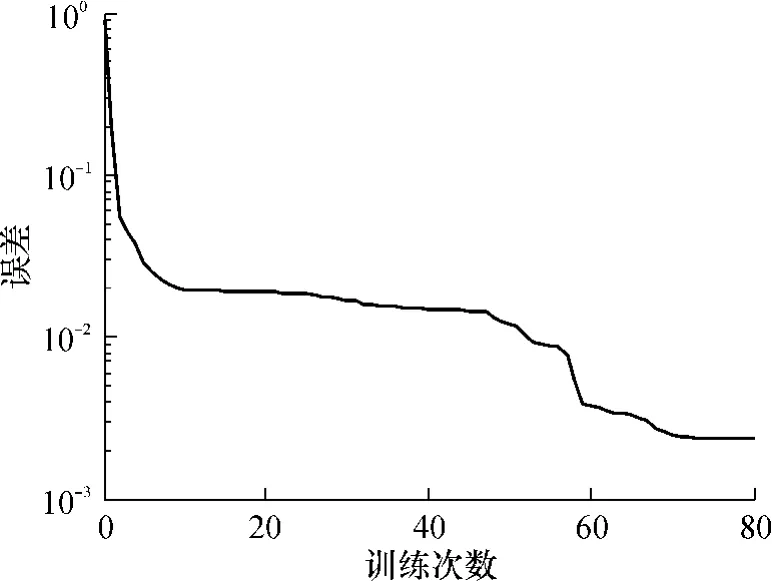
图2 神经网络训练误差Fig.2 Training error of neural network

图3是转速一定时，排气温度随油耗率变化的关系曲线，图中中间段样本数据和模型数据基本重合，两端数据偏差稍大，模型和样本平均偏差0.2%(排气温度实验值与辨识模型计算值之差占排气温度实验值的百分比)，最大偏差小于1.0%，满足分析计算要求.由图3可见，随着油耗率的增大，排气温度升高，因为油耗增加，燃料产热量增加，符合柴油机排气温度估计式.

图3 转速为2000r/min时排气温度随油耗率的变化规律Fig.3 Exhaust temperature varying with fuel consumption speed at an engine speed of 2000r/min

图4为转速一定时，排气温度随负荷变化的关系曲线.由图4可知，模型数据和样本数据基本重合，平均偏差0.12%，最大偏差小于0.50%，满足分析计算要求.由图4还可以看到，随着负荷增大，排气温度也相应升高.

图4 转速为2000r/min时排气温度随负荷的变化规律Fig.4 Exhaust temperature varying with load at an engine speed of 2000r/min

图5是油耗率一定时，排气温度随转速变化的关系曲线.由图5可知，模型数据和样本数据略有偏差，平均偏差为0.8%，最大偏差小于1.0%，满足分析计算要求.图5中数据说明随着转速的增加，排气温度降低.

图5 油耗率为0.43g/s时排气温度随转速的变化规律Fig.5 Exhaust temperature varying with engine speed at a fuel consumption speed of 0.43g/s

3 EGR温度模糊控制算法

有研究表明，EGR 最佳温度为 400 K［1］，一般EGR温度控制在393～433K之间.一部分排气引入进气系统即形成EGR气体，排气温度在柴油机不同工况下其数值变化范围大，不利于EGR效果，因此需要控制EGR循环温度.EGR温度影响因素复杂，控制模型不容易建立，在此利用模糊控制算法实现EGR温度的控制.

3.1 EGR温度控制模糊化

定义排气温度模糊子集为{NB，NM，NS，ZO，PS，PM，PB}，子集元素分别代表正大、正中、正小、零、负小、负中、负大，对应的实际EGR温度集合为{200＜T－400＜450，120＜T－400＜200，30＜T－400＜120，－10＜T－400＜30，－20＜T－400＜－10，－30＜T－400＜ －20，－40＜T－400＜ －30}，其中T为EGR控制前温度，单位为K.EGR温度控制输出模糊子集定义为{NB，NM，NS，ZO，ZO，ZO，ZO}，子集元素分别代表正大、正中、正小、零、零、零、零，对应实际中冷却电子扇转速由高到低7个档位.

隶属度函数定义成三角形，即符合式(3)，交叠系数取1.

式中:uF为隶属度函数;a、b、c分别为自变量x所属区域最小边界、中间点和最大边界.

3.2 模糊推理算法

根据模糊子集定义，设计EGR模糊规则算法:排气温度模糊集为{NB，NM，NS，ZO，PS，PM，PB}，对应控制输出模糊集为{NB，NM，NS，ZO，ZO，ZO，ZO}.即电子扇控制转速与排气温度对应，排气温度越高，电子扇转速越高，当排气温度接近EGR最佳温度范围时电子扇关闭.在本样例中控制电子扇在7 个档位工作，相应转速为{2300，2100，1900，1800，0，0，0}，单位为 r/min.

3.3 基于模糊推理算法的EGR温度控制

根据EGR模糊推理规则，设计EGR温度控制系统，其原理如图6所示.控制过程中电控单元(ECU)根据柴油机转速、负荷和油耗率输入，利用辨识模型估算排气温度，依据EGR温度模糊控制规则给出电子扇转速控制参数，实现EGR温度的自动控制.

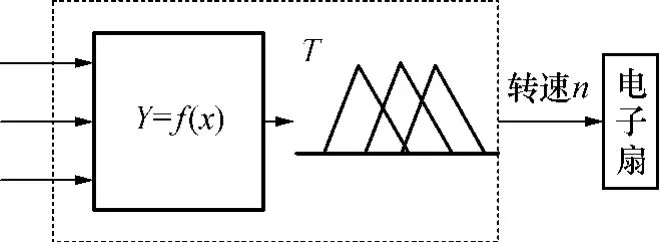
图6 EGR温度模糊控制原理图Fig.6 Principle of fuzzy control of EGR temperature

在柴油机台架控制器中嵌入上述电子扇控制算法程序，柴油机以2000 r/min由高负荷到低负荷运转.中低负荷时，排气温度保持在(400±10)K范围内;高负荷时，排气温度保持在(400±40)K范围内，满足EGR温度范围的要求.

4 结论

(1)从样机数据辨识结果可见，使用三层BP神经网络能够对柴油机排气温度辨识，模型辨识与实验测得的平均温度偏差在1.0%之内，满足计算要求.

(2)神经网络辨识模型建立时，需要结合物理模型，分析模型输入和输出参数的内在关系.由样机辨识结果可知，柴油机转速、负荷和油耗率影响柴油机排气温度，以三者为输入的神经网络模型可以获得柴油机排气温度的变化规律.

(3)实验和模型结果表明，转速一定时，负荷增大、油耗增大，排气温度升高;油耗和负荷一定时，转速降低，排气温度升高.

(4)将神经网络预测模型与模糊推理相结合，可以实现柴油机的EGR温度智能控制.

［1］ 房克信，邓康耀，邬静川.EGR温度对涡轮增压柴油机燃烧和排放的影响［J］.农业机械学报，2004，35(6):40-43.Xu Ke-xin，Deng Kang-yao，Wu Jing-chuan.Influence of EGR temperature on combustion and emissions of turbocharged diesel engine［J］.Transactions of the Chinese Society of Agricultural Machinery，2004，35(6):40-43.

［2］ Hountalas D T，Avropoulos G C，Binder K B.Effect of exhaust gas recirculation(EGR)temperature for various EGR rates on heavy duty DI diesel engine performance and emissions［J］.Energy，2008，2(33):272-283.

［3］ 周小祥，薛银春.基于小波分析的燃机排气温度传感器组故障诊断方法研究［J］.燃气轮机技术，2008，21(4):36-39.Zhou Xiao-xiang，Xue Yin-chun.Research of fault diagnosis of sensor group based on wavelet analysis［J］.Gas Turbine Technology，2008，21(4):36-39.

［4］ 黄鑫，刘忠民，俞小莉，等.发动机排气量测量方法比较研究［J］.车用发动机，2006(3):50-52.Huang Xin，Liu Zhong-min，Yu Xiao-li，et al.Study of engine exhaust heat measurement［J］.Vehicle Engine，2006(3):50-52.

［5］ 张豫南，葛蕴珊，徐春龙，等.BP和RBF神经网络在辨识内燃机燃烧过程中的应用［J］.车用发动机，2003(2):13-15.Zhang Yu-nan，Ge Yun-shan，Xu Chun-long，et al.Identification of diesel combustion process by BP and RBF neural network ［J］.Vehicle Engine，2003(2):13-15.

［6］ 梁锋，冯静，肖文雍，等.BP神经网络在高压共轨式电控柴油机故障诊断中的应用［J］.内燃机工程，2004，25(2):46-49.Liang Feng，Feng Jing，Xiao Wen-yong，et al.Application of BP neural network to fault diagnosis of high-pressure common rail fuel system of electronic control diesel engines［J］.Chinese Internal Combustion Engine Engineering，2004，25(2):46-49.

［7］ Adnan Parlak，Yasar Islamoglu，Yasar Halit，et al.Application of artificial neural network to predict specific fuel consumption and exhaust temperature for a diesel engine［J］.Applied Thermal Engineering，2006，26(8):824-828.

［8］ Al-Alawia Ali，Al-Alawia Saleh，Islam Syed M.Predictive control of an integrated PV-diesel water and power supply system using an artificial neural network ［J］.Renewable Energy，2007，32(8):1426-1439.

［9］ García-Nieto S，Salcedo J，Martínez M.Air management in a diesel engine using fuzzy control techniques［J］.Information Sciences，2009，179(19):3392-3409.