三维非线性轮胎的五刚特性仿真*

臧孟炎 许玉文 周涛

(1.华南理工大学机械与汽车工程学院∥广东省汽车工程重点实验室，广东 广州510640;2.华南橡胶轮胎有限公司，广东广州511486)

轮胎刚度作为轮胎最重要的力学性能参数一直备受汽车设计者的关注，它不仅影响到汽车的动力性、转向操纵性及制动安全性等［1］，而且是整车设计分析不可或缺的参数之一.目前考虑轮胎大变形引起的几何非线性、橡胶材料的物理非线性及接触非线性的三维非线性有限元分析是轮胎性能研究的热点［2-4］.

利用有限元法研究轮胎刚度性能取得了很多应用成果［4-8］.杨卫民［4］在 ANSYS 软件中建立子午线三维有限元模型，较好地模拟了充气轮胎在不同垂直载荷下与地面的接触情况.石琴、胡林等［5-6］深入分析了轮胎静、动态刚度的形成机理，探讨了径向、侧向及侧偏刚度与变形之间的关系.景立新［7］充分考虑轮胎橡胶材料和接触的非线性，使用简单纵沟槽花纹轮胎确认了径向、侧向和扭转刚度仿真与试验结果的基本一致性.应卓凡等［8］得出了限元模型是否考虑复杂花纹对轮胎径向刚度的仿真结果影响不大的结论.但是，以上对轮胎刚度性能的分析都局限在部分刚度上，缺乏对轮胎五刚特性，即径向、侧向、纵向、扭转和包覆刚度的全面仿真分析.文中以华南橡胶轮胎有限公司生产的175/65R14型子午线轮胎为研究对象，使用光面轮胎有限元模型，应用非线性有限元软件ABAQUS进行五刚特性仿真分析，以确认分析软件和仿真方法的有效性.

1 轮胎刚度特性

轮胎刚度特性是指作用在轮胎上的载荷与对应的变形之间的关系.文中分别针对径向、侧向、纵向、扭转及包覆进行刚度仿真分析，并通过与试验结果的比较确认仿真方法的有效性.

五刚特性的测试原理如图1所示，箭头所指方向为路面(包覆刚度为凸块)移动方向.

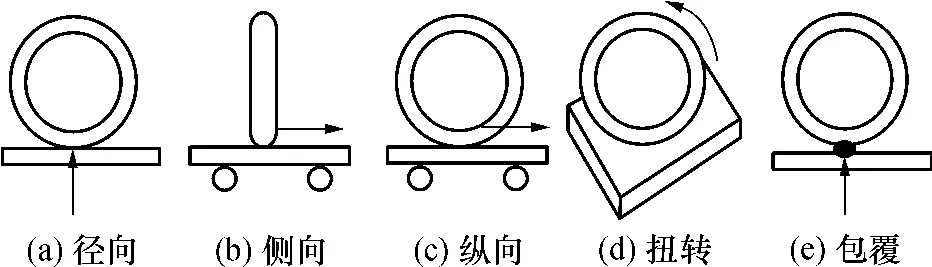
图1 轮胎五刚特性测试原理图Fig.1 Schematic diagram of characteristics test of five kinds of stiffness for tire

2 有限元模型的建立

2.1 几何模型和网格划分

研究表明［8］，轮胎花纹对轮胎静态刚度特性的影响甚微.为提高建模和计算效率，文中忽略花纹的影响，使用光面轮胎进行五刚仿真分析.利用光面轮胎的轴对称性，使用AutoCAD建立轮胎截面的二维几何模型，采用Hypermesh进行二维有限元网格划分.为避免划分网格时生成过多的变形单元［9］，从而有效提高网格质量和减少单元数量，文中对轮胎径向截面形状做了如下简化和修改:(1)在胎侧和钢丝带束层的邻接部位，把狭长尖角改成倒角;(2)胎侧和翼胶的材料特性相同且位置临近，将其合并.

将二维网格保存为ABAQUS命令行文件(inp文件)后，再利用 ABAQUS提供的*SYMMETRIC MODED GENERATION命令生成三维有限元网格.三维有限元网格的生成需保证几何结构的对称性，同时兼顾计算效率和收敛性:非接地区域轮胎网格的周向尺寸较大，接地区域轮胎网格的周向尺寸较小.文中采用的有限元网格如图2(a)和2(b)所示.

图2 轮胎的有限元网格Fig.2 Finite element mesh of tire

2.2 材料模型及单元类型的确定

轮胎材料主要由橡胶和帘线－橡胶复合材料组成.胎面、胎侧、三角胶、内衬层和胎圈护胶等使用硬度不同的橡胶材料，胎体、带束层、冠带层和胎圈使用帘线－橡胶复合材料.

橡胶材料属于超弹性材料，表现出近似体积不可压缩性和高度非线性，通常用应变势能U来表示其应力－应变关系.Yeoh模型因能较好地模拟橡胶材料大变形时的应力－应变关系而得到广泛使用.其本构方程如下:

式中，Jel为弹性体积比为扭曲度量，Ci0、Di(i=1，2，3)为Yeoh模型参数.

橡胶材料力学特性的表征效果不仅与材料的本构模型有关，而且受变形范围的影响［10］.利用同一材料模型，选取不同变形范围的试验数据进行拟合得到的材料参数也不同.考虑到轮胎刚度试验中橡胶材料的最大应变均不超过100%，故文中选取最大应变100%的单轴拉伸应力－应变数据拟合Yeoh模型材料参数，拟合数据如表1所示.

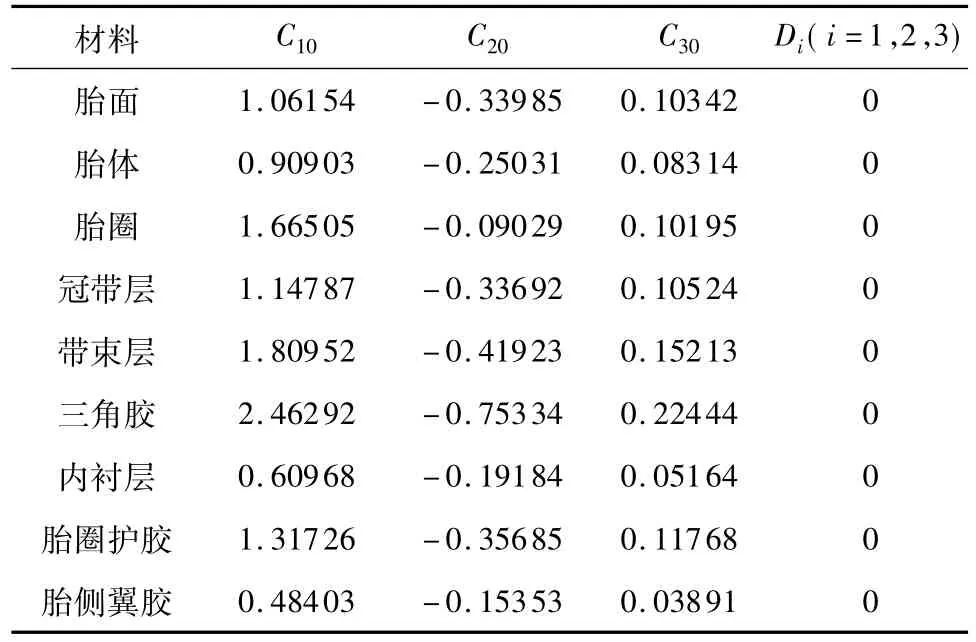
表1 橡胶材料Yeoh模型材料参数Table 1 Rubber material parameters in Yeoh model

带束层、冠带层、胎体、胎圈均使用帘线－橡胶复合材料，具有明显的各向异性.ABAQUS提供的加强筋(Rebar)模型能较好地模拟这种复合材料［10］.具体方法是先将Rebar单元定义在面单元上，再将该面单元嵌入到相应的橡胶实体单元内.同时，还需定义图3所示的Rebar层的参考面、法线方向以及偏离参考轴的初始角度、单根加强筋的横截面积和加强筋间距3个Rebar特性参数.这种方法不但可以准确模拟钢丝帘线在橡胶实体单元网格划分中的位置，而且可以分别定义模型中橡胶基体和钢丝帘线的材料参数，从而避免了复杂的复合材料参数的计算问题.

图3 加强筋的定义Fig.3 Definition of rebar

考虑到研究对象的几何形状、载荷条件、橡胶材料的近似不可压缩性及计算的收敛性等因素，轴对称模型中的四边形和三角形单元分别采用CGAX4H和CGAX3H单元，其对应三维空间单元采用C3D8H和C3D6H单元.

2.3 边界条件和加载方式

接触问题是有限元分析的关键，软件ABAQUS具有强大的接触计算能力.在接触边界条件的模拟中，为提高计算精度同时兼顾计算效率，采取了以下措施:

(1)将轮辋和路面定义为解析刚体简化模型;

(2)在二维轮胎充气分析中，轮圈和轮辋采用无摩擦接触;

(3)三维非线性分析采用面－面接触方式定义接触，选用直接约束法处理接触问题.

进行二维轴对称分析时，先给轮胎两侧胎圈部分沿轴向一定的相向位移，使之进入轮辋内侧，再在轮胎内表面施加均匀分布的法向压力，实现轮胎的安装充气过程.ABAQUS中的*SYMMETRIC RESULTS TRANSFER命令可实行二维应力应变向三维模型的传递，但需要一个分析步实现模型的三维平衡(保压过程)后，才能后续加载.五刚仿真时将轮辋固定，以对地面施加强制位移的方式进行预加载，然后以向地面施加作用力的方式进行精确加载，这样可以有效地提高计算的收敛性和稳定性.

2.4 非线性求解和收敛性分析

由于轮胎几何结构的复杂性和材料的多样性，利用ABAQUS/Standard进行非线性分析求解时，收敛性非常重要.除网格因素和接触定义外，由于五刚分析中胎面单元将出现大的位移或转动，表现出明显的几何非线性，需要使用软件的几何非线性分析功能.

另外，文中模型的求解采用 Newton-Raphson法，将一个分析步分解为多个增量步，载荷以增量形式逐步施加，当计算遇到收敛困难时，根据实际情况适当减少子载荷步长将有利于收敛.

3 五刚仿真分析及结果评价

3.1 五刚仿真分析

文中分别针对径向、侧向、纵向、扭转及包覆进行刚度仿真分析，并与试验结果进行比较.轮胎的五刚特性全部采用台湾弘达仪器股份有限公司生产的keD·TEK轮胎五刚试验机进行测试，试验装置如图4所示.

图4 轮胎刚度试验装置Fig.4 Device of stiffness test of tire

保持0.2 MPa的轮胎内压并固定轮辋，垂直向上移动地面以向轮胎施加径向载荷.径向刚度特性的仿真结果与试验结果如图5所示.

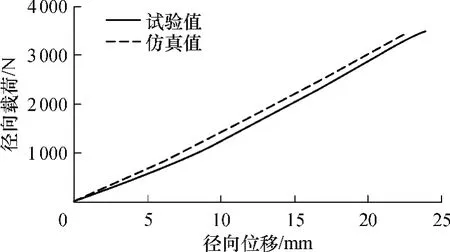
图5 径向刚度特性曲线Fig.5 Characteristic curve of radial stiffness

保持0.2MPa胎压且固定轮辋后向上移动路面实现汽车自重径向加载，然后侧向移动路面实现侧向加载.轮胎侧向刚度特性仿真结果与试验结果如图6所示.

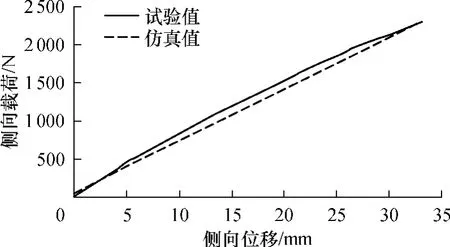
图6 侧向刚度特性曲线Fig.6 Characteristic curve of lateral stiffness

保持0.2MPa胎压且固定轮辋后向上移动路面实现汽车自重径向加载，然后纵向移动路面实现纵向加载.纵向载荷作用下轮胎纵向刚度特性仿真结果如图7中虚线所示.

图7 纵向刚度特性曲线Fig.7 Characteristic curve of logitudinal stiffness

保持0.2MPa胎压且固定轮辋后向上移动路面实现汽车自重径向加载，然后根据试验要求转动路面使轮胎发生扭转变形.扭转变形中轮胎扭转刚度特性仿真结果与试验结果如图8所示.

图8 扭转刚度特性曲线Fig.8 Characteristic curve of torsional stiffness

保持0.2MPa胎压且固定轮辋后向上移动路面实现汽车自重径向加载，然后根据试验要求将路面上一个10mm宽的解析刚体(即凸块)向上抬升.凸块载荷作用下轮胎包覆刚度特性仿真结果如图9中虚线所示.

图9 包覆刚度特性曲线Fig.9 Characteristic curve of coating stiffness

3.2 仿真结果评价

从图5－9中可知，轮胎五刚仿真分析中，径向、侧向、纵向和包覆刚度特性的仿真结果与试验结果基本吻合，扭转刚度特性的趋势与试验结果趋势基本一致，但小于试验结果.其原因可能是仿真模型没有考虑轮胎表面花纹.花纹的主要作用是提高轮胎与地面的抓着力，花纹的有无对纵向和侧向刚度尽管也会有影响，但它对扭转刚度的影响更大，以至于光面轮胎有限元模型扭转刚度的仿真结果明显小于试验值.为确认此推测，文中追加分析了另外两款不同型号轮胎(轮胎1，205/55R16;轮胎2，195/50R15)的扭转刚度特性，如图10所示.从图10中的仿真曲线可知，与图8相似，仿真结果总是小于试验值.鉴于3款不同型号轮胎的仿真结果与试验结果间具有相似的关系，为了简化仿真计算模型以提高仿真效率，文中认为使用光面轮胎模型预测轮胎扭转刚度特性时可以对仿真结果进行适当修正.如文中将仿真结果放大1.25倍时，3个轮胎均获得了与试验基本一致的预测结果(参见图8和图10的预测值曲线).

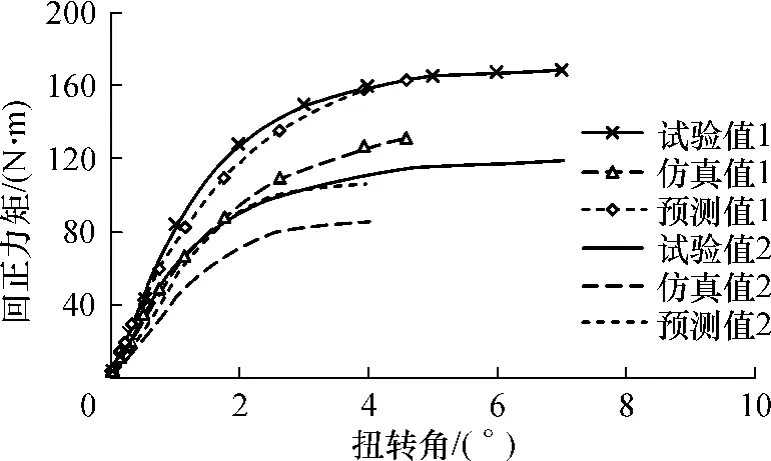
图10 其他两款轮胎的扭转刚度特性曲线Fig.10 Characteristic curves of torsional stiffness of other two tire models

4 结语

文中以175/65R14型子午线轮胎为研究对象，建立了在5种负荷作用下的三维有限元模型，在充分考虑轮胎的几何非线性、材料非线性及接触非线性等因素的基础上，使用ABAQUS软件模拟轮胎装配和充气过程，全面分析了轮胎的五刚特性，获得了具有工程应用价值的仿真预测结果.研究结果表明，使用仿真分析方法预测轮胎五刚特性是完全可能的，对于促进轮胎结构优化和整车性能的仿真评价具有重要意义.

［1］ 庄继德.汽车轮胎学［M］.北京:北京理工大学出版社，1996.

［2］ 丁剑平，贾德民，黄小清.三维非线性有限元法在子午胎分析中的应用［J］.华南理工大学学报:自然科学版，2005，33(6):55-58.Ding Jian-ping，Jia De-min，Huang Xiao-qing.Application of 3D nonlinear finite element method to the analysis of radial tires［J］.Journal of South China University of Technology:Natural Science Edition，2005，33(6):55-58.

［3］ Tseng N T，Pelle R G，Warholic T C.Finite element simulation of destructive tire testing［J］.Tire Science and Technology，1991，19(1):2-22.

［4］ 杨卫民.子午线轮胎的三维非线性有限元分析与性能仿真的研究［D］.北京:北京化工大学机械工程学院，1998.

［5］ 石琴，陈无畏，洪洋，等.基于有限元理论的轮胎刚度特性的仿真研究［J］.系统仿真学报，2006，18(6):1445-1449.Shi Qin，Chen Wu-wei，Hong Yang，et al.The simulation of tire's stiffness characteristics using finite element model［J］.Journal of System Simulation，2006，18(6):1445-1449.

［6］ 胡林，谷正气，黄晶，等.30.00R51子午线轮胎刚度仿真［J］.系统仿真学报，2008，20(8):2210-2214.Hu Lin，Gu Zheng-qi，Huang Jing，et al.Simulation of 30.00R51 radialtire's stiffness characteristics［J］.Journal of System Simulation，2008，20(8):2210-2214.

［7］ 景立新.全钢载重子午线轮胎特性有限元分析及验证［D］.吉林:吉林大学汽车工程学院，2007.

［8］ 应卓凡，臧孟炎，周涛.基于复杂花纹的子午线轮胎刚度特性仿真 ［J］.汽车技术，2009，30(11):35-37.Ying Zhuo-fan，Zang Meng-yan，Zhou Tao.Simulation analysis of radial tire's stiffness characteristics considering detailed tread blocks［J］.Automotive Technology，2009，30(11):35-37.

［9］ 郭孔辉，刘青.考虑胎体复杂变形的轮胎稳态侧偏特性理论模型 ［J］.机械工程学报，1999，35(2):15-18.Guo Kong-hui，Liu Qing.Theoretical model of steady state tire cornering properties with the complex deformation of carcass under considerration［J］.Chinese Journal of Mechanical Engineering，1999，35(2):15-18.

［10］ 应世洲，陈方，王国林.基于rebar单元的载重子午线轮胎模型建立及验证［J］.轮胎工业，2007，27(8):462-465.Ying Shi-zhou，Chen Fang，Wang Guo-lin.TBR tire modeling and validation based on rebar element［J］.Tire Industry，2007，27(8):462-465.