浅议弹簧教学
2011-01-24刘景世
刘景世
(宝鸡文理学院物理系 陕西 宝鸡 721013)
弹簧是一种利用弹性来工作的机械零件.利用它的弹性可以控制机件的运动、缓和冲击或震动、贮蓄能量、测量力的大小等.它广泛用于各种机械、仪表中,因此不论在中学物理教学或大学物理教学中均处于十分重要的地位.在弹簧的教学中如何较为全面地向学生介绍相关知识,使学生对这部分知识理解深刻,应用熟练呢?本文拟从弹簧力学模型特征、弹性势能零点选取讨论等四个方面加以分析、总结.
1 弹簧力学模型特征
在力学中经常涉及到“轻绳”、“轻杆”和“轻弹簧”模型,“轻绳”、“轻杆”及“轻弹簧”是由各种实际情况中的绳、杆和弹簧抽象出来的理想物理模型.由于“轻绳”、“轻杆”和“轻弹簧”这三种模型本身有着细微的差异,故表现出来的性质也有所不同.在分析弹簧力学模型特征时,不妨将这三种模型的特点加以对比,以加深对弹簧力学模型的理解.
1.1 三种模型的相同点
轻绳、轻杆和轻弹簧的“轻”(相对其他物体来说)就是指其质量可以忽略,所受重力可以忽略.它们对其他物体的作用力都是弹力,属接触力、被动力,都可以连接其他物体.
1.2 三种模型的不同点
1.2.1 作用力的效果
轻绳只能发生拉伸形变;轻杆、轻弹簧既能发生拉伸形变,也能发生压缩形变.故轻绳对物体只能是拉力,而轻杆、轻弹簧对物体既可以是拉力,又可以是支撑力(或压力).
1.2.2 作用力的方向
三者软硬程度不同:绳是软的,杆是硬的,弹簧介于二者之间.它们的形变方向有所不同:导致绳不能产生侧向力;弹簧在只发生拉伸或压缩形变而没有弯曲和扭转形变,可认为不能产生侧向力;而杆能产生侧向力.故轻绳上的作用力一定沿着绳子的方向,轻弹簧上的作用力一般认为沿弹簧长度方向,而轻杆上的作用力却不一定沿杆的方向.
1.2.3 作用力的变化
轻绳、轻杆的劲度系数极大,受力形变极微,恢复形变不需要时间.轻弹簧的劲度系数不是十分大,受力后形变较大,恢复形变需要一段时间.故轻绳、轻杆对物体的作用力能发生突变,而轻弹簧对物体的作用力却不能发生突变.
1.2.4 形体的变化
轻绳、轻杆的形变极微,故轻绳可认为是不可伸长的,但绳是软的且可以松弛;轻杆可认为是不可能伸长或压缩,其长度是不变的;轻弹簧的形变较大,其长度可以变化.
1.2.5 能量的变化
由于轻杆硬且直,所以用轻杆连接的系统的机械能一般认为不变;轻绳被拉直的过程中尽管时间极短,但用其连接的系统的机械能有损失,常常转化为系统的内能;轻弹簧在弹性形变范围内被拉伸或压缩的过程中,用它连接的系统机械能没有损失(不考虑摩擦),只是动能或重力势能与弹性势能相互转化,而没有转化为内能.
2 弹性势能零点选取讨论
在动力学教学中,我们常常应用机械能守恒定律
ΔEk+ΔEp=0
这时,就要考虑到如何选取势能零点的问题.如果势能零点选取恰当,解题过程就可以大为简化;对于弹性势能也不例外.现在笔者就弹簧的弹性势能及简谐振动系统中势能零点选取问题进行分析、总结.
2.1 弹簧的弹性势能成立的条件
对于弹性系统,通常规定弹簧无任何形变(不伸长也不缩短)时势能为零,那么弹簧伸长或缩短x时系统的弹性势能为

以竖直放置的弹簧振子为例,在不计弹簧质量和阻力的情况下,可以证明在平衡位置附近的振动是简谐振动,且其动力学、运动学方程的形式与水平放置的弹簧振子的形式完全相同.
当我们把弹簧的弹性势能零点选取在距离弹簧原长端点处为x1的位置时,若弹簧在x1的基础上又伸长了x时,经过简单推导易知此时弹性势能为
此时Epe而x为振子相对于新的弹性势能零点的位移.由于x具有任意性,故选取x1处为弹性势能零点时,其他任意点的弹性势能为
弹簧处于原长时,x=-x1,此时弹性势能为
由此可见,取任意点作为弹性势能零点,弹性势能可以出现负值.
2.2 简谐振动系统总势能成立的条件
我们经常遇到在诸如重力等恒外力作用下的简谐振动问题.仍以竖直放置的弹簧振子为例,在力学教材[1~2]中,讲解简谐振动的能量转换时,一般是以水平光滑桌面上的弹簧振子为例讨论振动系统的动能、势能随时间变化规律,并计算总机械能.其振动位移表达式和机械能表达式分别为
x=Acos(ωt+φ)
和

3 弹簧连接体运动浅析
在物理教学中常见一些与弹簧有关的问题.由于弹簧形变发生时弹力会发生变化,使得与弹簧连接的物体受力发生变化,从而使物体的运动状态变化复杂.但是只要我们弄清其变化的临界状态,再通过分析受力情况便可求得结果.在这里分析物理过程是一个难点,因为较复杂的物理过程往往是由彼此联系的几个分过程综合而成的.因此教学中应注重培养学生对物理过程的分析,找出前后联系的纽带.
3.1 弹簧受力不能突变时的连接体临界问题
应用知识点:弹簧由于自身特殊结构,使得其发生形变产生弹力时,弹力不能由某一值突变为零,或由零突变为某一值.
3.2 弹簧在不同长度时的连接体临界问题
与弹簧连接的物体在运动过程中由于状态的变化,从而使弹簧在某时刻最长,某时刻处于原长,某时刻最短,整个过程是动态的.求解这一类问题通常是先对物体受力分析,再结合物体的运动状态和运动过程,分析弹簧什么时刻最长,什么时刻最短,什么时刻处于原长,然后求出其临界值.
总之在解答弹簧连接体一类问题时,一般都是先对物体进行受力分析,找出物体的临界状态,结合动量定理、机械能守恒定律及牛顿第二定律;有些特殊情况还要用到简谐振动的规律求解.
4 弹簧等效质量探析
反映弹簧振子系统重要特性的是它的周期公式
(1)
式中M是振子质量,κ是弹簧的劲度系数.教材对(1)式成立的条件作了明确界定:弹簧是理想的或轻质的,即弹簧自身质量可以忽略不计.当这个条件不成立时,周期公式又该如何表述?这就涉及到弹簧的等效质量问题.许多文献从多种角度出发导出弹簧振子振动的周期公式为
式中me为弹簧的等效质量.此周期公式说明:当把弹簧的等效质量加到弹簧振子的质量上时,才能把弹簧振子视为理想的振动系统.文献[3~4]通过分割法或积分法推导出
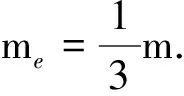
当m≪M时
当m≫M时
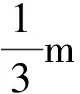
如今,随着科学技术的发展和进步,弹簧的种类日益增多,其使用范围也更加广泛,弹簧在物理教学中的重要地位也更加突出.
参考文献
1 漆安慎,杜婵英.普通物理学教程·力学.北京:高等教育出版社,2002.259~269
2 程守洙,江之永.普通物理学(第三册).北京: 高等教育出版社,1998.18~19
3 刘怀宜.弹簧的等效质量研究.重庆工学院学报,2001,15(2):98~100
4 漆安慎,杜婵英.力学.北京:高等教育出版社,1997.268~269
5 张庆海,潘华锦,齐建英.用最小二乘法测弹簧的有效质量.大学物理,2002,21(11):33~34
6 付茂林,刘世清.非线性形变对弹簧等效质量的影响.广西物理,2002,23(1):36~37
