弹性地基梁法在被动桩问题反分析中的应用

梁 墨， 陈福全

(福州大学 土木工程学院， 福建 福州 350108)

目前，研究被动桩与土体相互作用的分析与设计计算方法主要有四种：经验法，基于土压力的分析方法，基于土体变形的分析方法和有限单元法。经验方法主要是根据实测资料建立堆载与桩基位移或最大弯矩的经验图表，没有考虑土力学原理，没有考虑土体条件、堆载形状，因此拟合曲线离散性较大，很难推广应用；基于土压力的分析方法简便实用，但没有考虑桩土相互作用和变形的非线性，只能作为被动桩的初步设计；有限元法虽然能够考虑复杂的土体和堆载条件，但由于土体模型和参数确定困难，目前只能作为参数研究的辅助手段[1～3]。弹性地基梁法属于基于土体变形的分析方法，与其他方法相比，是求解水平受荷桩的实用方法，不仅能反映桩土之间的相互作用，而且计算简便，有大量的参数选取经验[4]。

本文对冯紫良[4]等弹性地基梁计算程序进行改编，增加的功能包括土压力计算、弹性地基梁计算及支护结构和被动桩的刚度、刚度基床系数和土压力系数的反演，可用于地面堆载下邻近单桩性状的计算。

1 弹性地基梁法计算模型

在地面堆载作用下，被动桩受到桩前土的挤压而发生变形和位移，同时变形的被动桩推挤桩后的土体，从而桩后土体也发生变形，并对桩施加了被动抗力。弹性地基梁法就是将桩后的土体假定为Winkler弹性地基，土体等效为连续分布的弹簧，如图1所示。

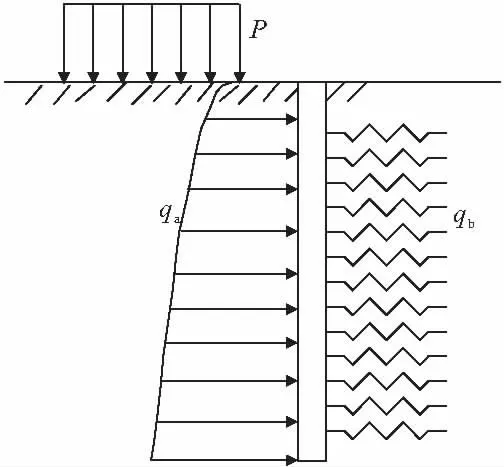
图1 弹性地基梁法计算模型

1.1 桩前临荷侧土压力

土体在地面堆载的作用下发生位移挤压而在桩身产生的土压力比较复杂，有不少学者[2]通过实验和理论推导来探求被动桩的土压力大小及分布形式，总结了一些结论。如：黄伟达和Ito等[5～7]根据塑性变形理论从单排桩角度推导出了移动土体产生的极限侧压力计算公式，沈珠江[8]利用散体极限平衡理论推导了土体沿水平方向绕桩滑动时桩身受到的绕流阻力公式等。

在程序中，不考虑土体绕桩滑动，由于桩间土拱效应的存在，按EI相等将单排桩等效成板桩，并且桩后土体被Winkler弹性地基取代。桩前临荷侧土压力qa可以近似用挡土墙的朗肯主动土压力与地面堆载产生附加应力的总和计算。其中朗肯主动土压力部分的计算按土力学中方法进行。

王国粹[9]在研究路堤堆载对邻近桥梁桩基影响时，将地面堆载在桩身产生的附加应力用基于弹性理论的Boussinesq解来解答。本文编制程序时参考了这一做法，假设邻近荷载形状均布的条形荷载，地基内任一点的内力可以用Boussinesq解的积分形式求得。即条形荷载下地基中任意点M处的附加水平应力如下

(1)

其中，参数β1,β2如图2所示。

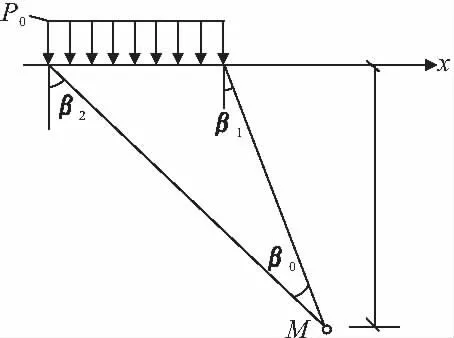
图2 Boussinesq解参数β1,β2示意图

1.2 桩后土抗力

根据弹性地基的局部变形理论，地基土对桩的反力强度qb与桩的侧向变形y之间的关系为

qb=kby

(2)

式中，kb为地基系数(kN/m3)，表示单位体积土在弹性限度内产生单位变形时所需加的力，可用m法计算，即kb=mz，m为地基反力系数(kN/m4)；z为计算深度(m)。本文分析m时的取值参考《公路桥涵地基与基础设计规范》[10]，取该规范建议值的平均值。

2 弹性地基梁法有限单元求解

2.1 桩的离散

将被动桩作为弹性地基梁，可用两节点单元来进行离散，如图3(a)所示，以节点1，2，…，n+1将桩分为n个单元，桩和土的接触面也分为n个子域。设第i单元长度为li，桩宽度为Bi，两端节点未知量为：侧向位移yi和转角θi，即任一节点i的位移wi可表示为

(3)

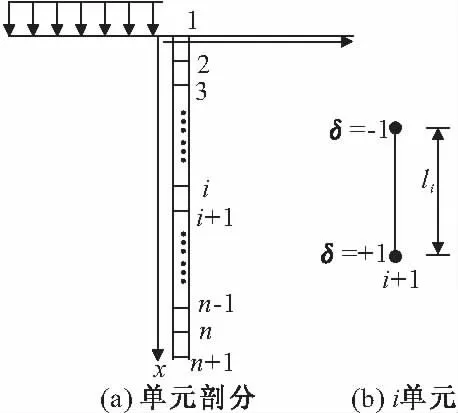
图3 桩离散示意图

在每个单元内设立局部坐标ξ，单元两端节点处的坐标分别设为ξ1=-1,ξ2=+1，如图3(b)所示，局部坐标与整体坐标有以下换算关系：

(4)

式中li为单元长度，xc为单元中点的总体坐标，其中li=x2-x1。

(5)

对式(4)取导数，可得到局部坐标与整体坐标之间的导数关系式：

(6)

于是对任意函数f有：

(7)

对应的梁单元位移函数及其对应的边界条件参见文献[4]。

2.2 单元能量公式

任意一纯弯梁单元e的总势能由单元的弯曲应变能和外力势能组成：

(8)

式中qa为被动桩临荷侧土体位移引起的侧向压力；qb为被动桩背荷侧土体抗力；式(8)中右端第一项为桩弯曲势能，第二项为临荷侧土压力势能，第三项为地基土的变形对结构体系总势能的贡献Id。局部坐标与总体坐标系间的导数有下列关系：

(9)

从而得到：

(10)

式中B为单元的应变位移矩阵：

w为单元的节点位移向量：

根据最小势能原理，为使Ie达到极小值应有：

(11)

解(11)方程组得：

(12)

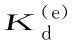
K(e)

单元节点荷载F(e)为：

(13)

按通用的对号入座的方法可集成桩的整体刚度[K]、位移向量{W}以及节点荷载向量{F}，从而得到桩的整体平衡方程：

[K]{W}={F}

(14)

2.3 程序中反演参数的有限元原理

通常在求解岩土工程问题中，反分析是利用工程中实测值(如应力、位移等)，通过数值计算确定岩土介质的力学参数，有时甚至是本构模型反演，求得问题所需的物理量。参数反分析方法可分为逆反演法和正反演法。本文采用正演方法确定力学参数，即把数值分析方法和数学规划结合起来，通过不断修正介质的未知数，使得一些现场实测值与相应的数值分析计算值的差异达到最小。正演法不像反演法那样需要重新推导数值分析的方法。反分析中正演法具有较强的适应性，能处理各种类型的反分析问题，可以应用于各种非线性问题。

在正演法中，把一些实测值(如位移、应力等)与相应的数值分析计算值之差的平方和作为目标函数F，即

(15)

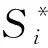
上式中Si是随土体的力学参数{p}n的变化而变化，n为独立变化的需要通过反分析确定的参数总数。可认为Si是参数{p}n的函数，目标函数F为参数{p}n的函数。因此，反分析计算转化为求目标函数的极小值问题。当目标函数F得到极小值时，其所对应的参数{p}n就是反分析所需要得到的最优参数，即

(Pj)opt=Pj当F(P)opt=min[F(P)]

(16)

为了平衡大小值之间作用和消除不同物理量的量纲，目标函数采用如下形式

)2

(17)

对同一命题不同的目标函数形式通常会有不同的反演结果。用实测位移反分析计算位移可以得到很好的结果，但计算内力可能较差。然而，用内力反分析可以得到较好的内力和位移。采用不同的物理量会有不同的反分析效果，在目标函数中对不同的量赋予不同的权数，可望达到更好的反演效果：

(18)

式中kj为目标函数实测值的权数。

通常以上目标函数是介质力学参数{p}n的复杂的非线性函数，一般无法采用解析法求解。上述方程可采用多种方法求解，如直接法、共轭方向法、变尺度法、单纯形法、模式探索法等。

2.4 程序功能

程序采用FORTRAN语言编制，可用于地面堆载下被动桩性状的计算。可以根据地面堆载情况和土层信息正演计算出被动桩临荷侧桩身土压力，桩身位移，弯矩等数据；也可以通过已量测的部分桩身位移反演计算得到土体的地基反力系数和临荷侧桩身土压力，进而计算出更加准确的结果。

3 算例

为了验证程序的正确性，本文用PLAXIS8.5和所编程序的正算与反演结果进行对比。

3.1 概况

如图4所示，算例为单排被动桩，桩顶自由无约束，桩长为20 m，桩截面为圆截面，桩径为0.7 m，泊松比为0.167，桩身刚度为2.0×107kPa，将被动桩等效为板桩后取板桩等效模量为1.0×107kPa，桩头自由。堆载为均布荷载，作用区域宽10 m，距桩顶中心距离为2.0 m，堆载大小取为60 kPa。模型左右计算范围取60 m，由于软土层厚度达10 m，桩土间可不设置介面单元[11]。

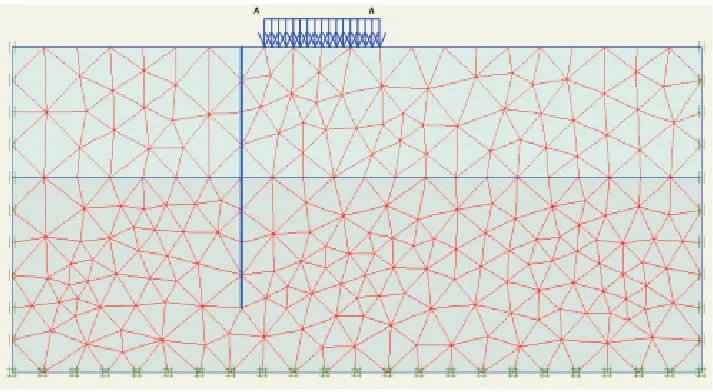
图4 有限元模型

算例有两种土层，上层是软土层(淤泥质粘土)，厚度为10 m，下层是硬土层(粉砂夹砂质粉土)，厚度为15 m。有限元分析时土体的本构模型采用HSS模型，相关参数来自上海地区深基坑开挖时试验得到的土层参数。

HSS模型在有限元计算中需输入以下参数：刚度依据某个幂率的应力相关性，输入参数m；主偏量加载引起的塑性应变，输入参数E50；主压缩引起的塑性应变，输入参数Eoed；弹性卸载/重加载，输入参数Eur；考虑小应变情况，输入参数G0，γ0.7；依据Mohr-Coulomb模型的破坏模式，输入参数c，φ。表1为计算参数。

表1 土体计算参数表

本例中桩基在地面处位移最大值超过了6 mm，规范中指出当位移较大时，应适当降低。所以算例中m的取值参考了王国粹[9]的取法，他通过计算多组m值组合桩身变形的综合对比分析表明：选取海湾淤泥m1=1000 kN/m4，亚粘土m2=40000 kN/m4，弱风化花岗岩m3=60000 kN/m4是合理的。结合规范和王国粹的取法，本例中软土层m在表1中取值范围为3000～5000 kN/m4，适当取小后取m1=2000 kN/m4，硬土层m取值范围为10000～20000 kN/m4，适当取小后取m2=10000 kN/m4。

3.2 正算结果比较

图5给出了计算结果，表明用弹性地基梁法编制的程序与用PLAXIS数值分析得到的结果近似。桩身的位移主要发生在软土层，最大位移在桩顶处，桩身的最大正负弯矩分别在软硬土层的交界处和软土层中部附近。图5(a)表明用弹性地基梁程序算出来的位移要比数值分析得到的结果略小。这是因为弹性地基梁法采用弹性假设，没有考虑塑性变形，而有限元分析用到了弹塑性本构模型，故其变形大；规范建议当桩基在地面处的位移大于6 mm时，要适当减小土体地基反力系数m的取值[10]，由于缺乏相关经验且适当减小的幅度没有具体的标准，所以导致程序计算所取m比现实中m要大，从而土体抗力越大，桩身变形就越小。同时土体地基反力系数m的取值，对弹性地基梁法计算被动桩的影响比较大。本文程序计算出来的临荷侧桩身土压力比有限元计算的要小，有必要通过反演方法来获得合适的m值和临荷侧桩身土压力值。

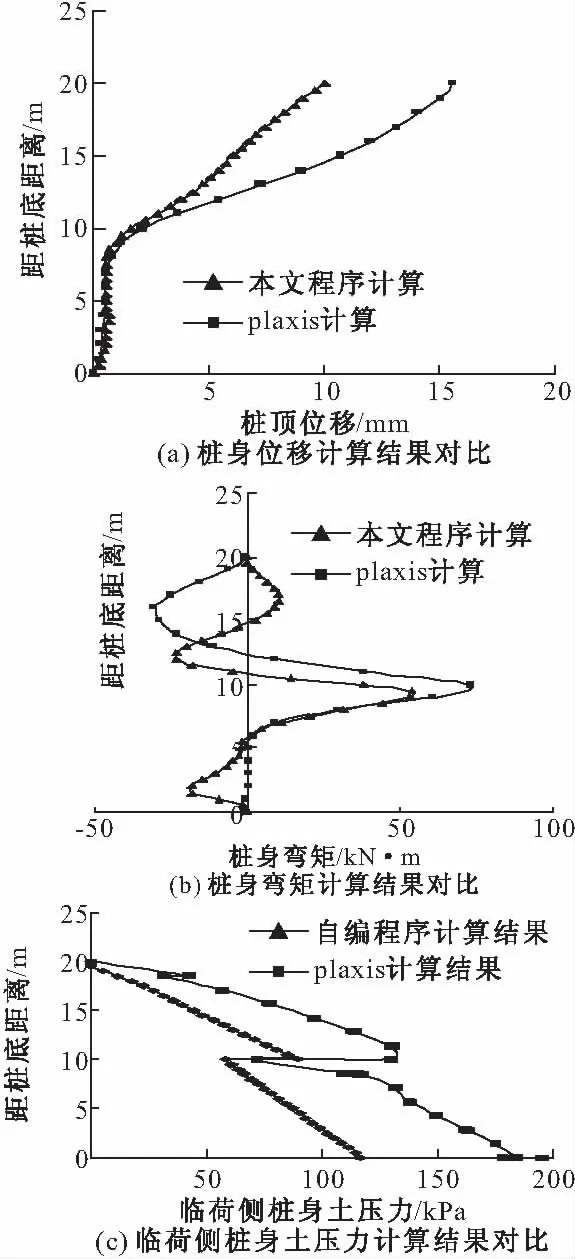
图5 本文程序与有限元计算结果比较

从图5(b)可见，弹性地基梁程序得到的结果与有限元分析的结果相近，但程序计算的桩身顶部和底部出现了不大的反向弯矩。可能的原因是在计算朗肯土压力时，桩顶处两个单元的土压力为负值，程序自动将桩前土压力负值取0，同时桩底处位移与转角指定为0造成，但结果对桩身最大弯矩值和分布位置影响不大。

3.3 反演计算结果对比

对于计算中不易确定的地基反力系数m，可以通过程序中的反演功能得到，进而得到桩身变形、弯矩等数据，另外临荷侧桩身土压力也可以通过反演获得。反演需要输入的数据是通过实测或计算得到的部分桩身位移，输入的不同部位桩身位移越多，越容易反演出准确值，但输入过多容易引起程序不收敛。

在实际工程中，桩顶在地表处的位移比较容易得到，所以算例反演时仅输入由PLAXIS计算得到的桩顶水平位移15.6 mm，来观察程序反演的效果。如果现场能得到更多的桩身位移，得到的结果将更准确。在这个算例中将同时反演地基反力系数和临荷侧桩身土压力，计算结果如图6所示。从图看出，反演计算得到的结果与PLAXIS计算的结果更加吻合，除桩顶处为反演输入的位移外，桩身位移也相差不大，最大正负弯矩值和临荷侧桩身土压力也更接近。

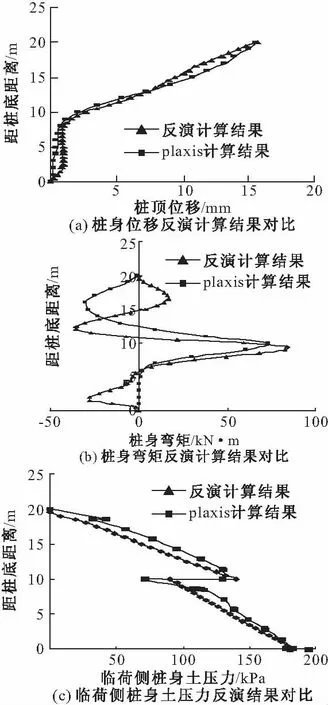
图6 反演计算结果与有限元结果对比

反演得到了dkcoef(1)、dkcoef(2)、qcoef(1)和qcoef(2)这四个参数，可以通过式(19)和(20)算出反演得到的m和临荷侧桩身土压力qa：

(19)

(20)

算例中，算得dkcoef(1)= 1、dkcoef(2)=1、qcoef(1)=1.56和qcoef(2)=1，算得m=m0，qa=1.56qa0。也就是说反演得到的地基反力系数等于输入值，而反演得到的临荷侧桩身土压力为正演计算qa结果的1.56倍。

在反演算例中同时反演了地基反力系数m和临荷侧桩身土压力qa。在实际工程中，如果已经通过现场试验等手段获得了准确的m值或qa值，也可将测得的数据输入程序而仅反演其中一个参数。在正演和反演计算中，允许手动输入已获得的临荷侧桩身土压力来取代程序本身的桩前土压力计算结果，从而使桩前土压力更符合实际而不局限于程序的假定形式。

4 结 论

(1)在桩身位移未知情况下，采用弹性地基梁法正演计算的结果与有限元的结果基本吻合，关键在于m值的选取和临荷侧桩身土压力qa计算的准确性。

(2)桩身的最大位移发生在桩顶处，桩身最大负弯矩发生在软土层中部附近，最大正弯矩发生在软硬土层交界处。

(3)桩身位移已知时，可用程序反演得到土体合适的地基反力系数m和临荷侧桩身土压力。另外本文程序可以对多层土体的m值进行反演。

(4)m法将土体看作弹性体，只适用于桩顶位移较小的情况。而桩的p-y曲线计算方法可以考虑土体的非线性行为，以后程序的改进可以考虑采用p-y方法。

[1] Fang Y S, Ishibashi I． Static earth pressures with various wall movements[J]．Journal of Geotechnical Engineering，1986，112(3)：317-333.

[2] Pan J L, Goh A T C, Wong K S, et al. Ultimate soil pressure for piles subjected to lateral soil movements[J]．Journal of Geotechnical and Geoenvironmental Engineering，2002,128(6)：530-535.

[3] Stewart D P，Jewell R J , Randolph M F．Design of piled bridge abutments on soft clay for loading from lateral soil movement[J]．Géotechnique， 1994，44 (2)：277-296.

[4] 冯紫良，戴仁杰.杆系结构的计算机分析[M].上海:同济大学出版社,1991.

[5] 黄伟达.堆载作用下被动桩与土体相互作用研究[D].福州:福州大学，2006.

[6] Ito T, Matsui T. Methods to estimate lateral force acting on stabilizing piles[J]. Soil and Foundations, 1975, 15(4):43-59.

[7] Ito T， Matsui T, Hong W P. Design method for stabilizing piles against landslide——one row of piles[J]. Soils and Foundations, 1981, 21(1):21-37.

[8] 沈珠江.桩的抗滑阻力和抗滑桩的极限设计[J].岩土工程学报,1992,14(1):51-56.

[9] 王国粹,杨 敏,熊巨华,等.路堤堆载对邻近桥梁桩基影响分析[J].结构工程师,2008,24(4):94-98.

[10]JTG D63-2007,公路桥涵地基与基础设计规范[S].

[11]陈福全.地面堆载作用下邻近桩基性态数值分析[D].上海:同济大学.2003.