调谐液柱阻尼器参数计算的简化方法

吕 川， 梅明荣

(河海大学 力学与材料学院， 江苏 南京 210098)

上世纪70年代， YAO[1]首先在工程结构中提出结构控制的概念，此后，许多学者做了大量的研究，并取得了卓越的成果。1980年， MODI[2]等首次提出利用调谐液体阻尼器(tuned liquid damper, TLD)来抵御结构风振，TLD是利用固定容器中液体的惯性力和粘滞力来耗能减少结构振动的减震装置，由于其构造简单，安装容易，造价低廉，基本不需要维护，使得TLD与其他阻尼器相比有更多优势，故近些年得到了学者们大量的研究[3～7]。

80年代末，Sakai[8]等第一次提出用调谐液柱阻尼器(tuned liquid column damper, TLCD)来减少结构水平振动，TLCD是一种特殊的TLD装置，其存储液体的容器是一个U型管，减震机理与TLD类似。目前已经有很多研究人员对其进行了研究，之前的研究都表明，只有当选取合适的参数,TLCD才能达到满意的减震效果，故参数的选择至关重要。Yalla[9]已经对TLCD参数的选择做了比较详细的研究，并且获得了白噪声荷载条件下的最优参数。

由于液体所固有的非线性液体阻尼特性，迭代法是获得TLCD结构系统频率范围的常用手法，但需要大量的计算，为了简化算法，节省时间，本文介绍一种TLCD结构参数优化计算的简便方法，并通过实例计算分析，证明这种简化计算方法是可靠的。

1 TLCD运动方程

图1所示的单自由度TLCD的运动方程可以表示为：

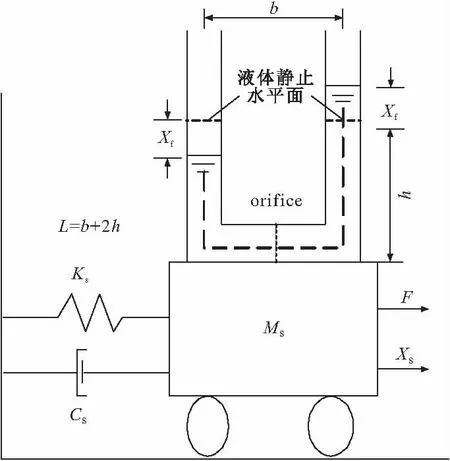
图1 TLCD单自由度结构

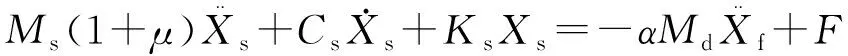
(1)

(2)

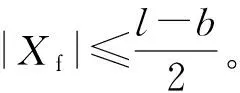
由于Cnon是一个非线性阻尼，利用统计线性方法[10]，可以用一个等效线性阻尼Ceq近似地代替非线性阻尼Cnon，替代后产生的误差表达式为：

(3)

欲使误差最小，则误差的均方差需满足：

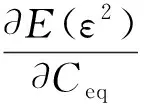
(4)

可以求出

(5)

在稳定的谐振状态下，Xf可以写成如下表达式

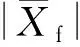
(6)

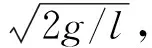
(7)

将Ceq代入方程(1)、(2)，可以得出如下矩阵形式：

(8)

传统的迭代法步骤为：给定设计参数ωs、ξs、δ、ωf，假定ξd的初始值ξd(0)，代入方程(8)，计算出Xf，再将Xf的值回代入等式(7)，求出ξd(n+1)的值，判断其是否满足精确度要求，如满足，则Xf即为所求精确解，如不满足，则继续迭代直至满足精度要求。

下面介绍用简化方法求液体位移，在谐振状态下，结构和液体的位移可以表示为：

结合等式(7)，将上式代入方程(8)，解方程可得到下列等式：

(9)

(10)

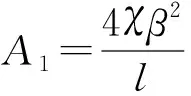
|A3|2=0

(11)

对无阻尼基础结构，Im(A2)=0，可以求出液体的位移幅值为：

(12)

2 分析比较

图2、图3分别给出了两种解法的流程图。通过对比两种解法的流程图，可以看出简化方法跳过了迭代步骤，直接求出阻尼器的位移幅值，进而求出液体等效阻尼。下面用实例来检验简化方法的精确度。

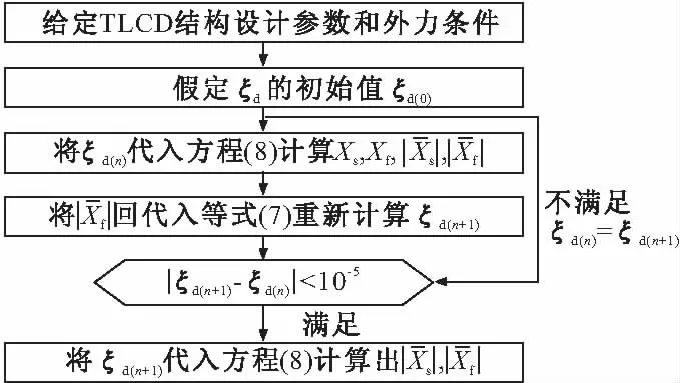
图2 迭代方法计算流程

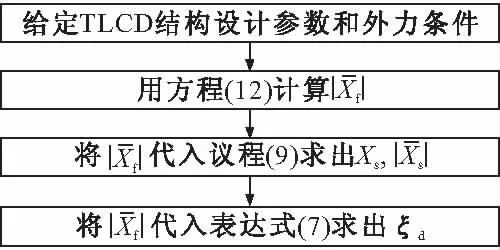
图3 简化方法计算流程

3 计算实例

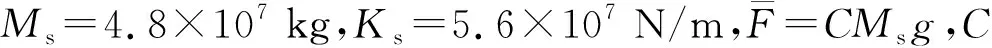
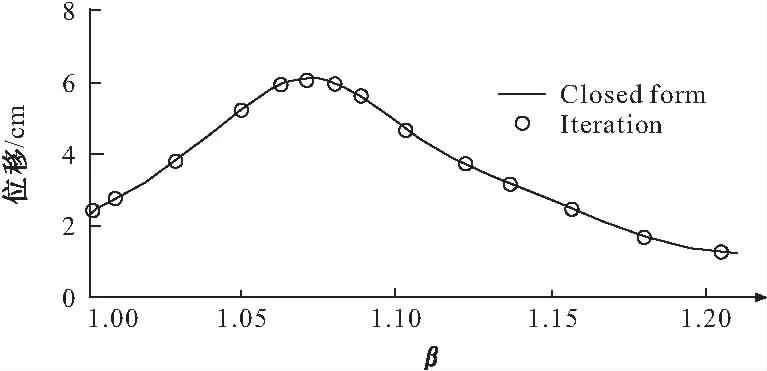
图4 ξs=0时结构位移幅值

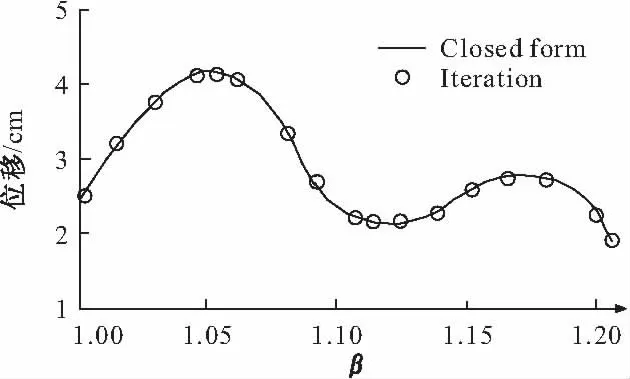
图5 ξs=0.02时结构位移幅值

由图4、图5可以看出，两种解法最终计算结果基本吻合，证明这种解法是准确可行的。

4 结 语

本文讨论了一种调谐液柱阻尼器参数计算的简化方法，用来代替原来的迭代法。以往，由于液体的非线性阻尼，通常会采用迭代法来计算TLCD结构系统的最优参数。本文先建立标准受力模型，推导出求解方程，然后将两种解法进行对比，证明简化方法的可行性。这种简化方法跳过了迭代步骤，能更快更方便地对TLCD系统做出初步的分析，为后面求阻尼器的最优水头损失系数、最优频率比以及最优阻尼系数提供了便利。

[1] Yao J T P.Concept of structures control[J].Journal of the Structural Division，1972，98(7)：1567-1574.

[2] Modi V J，Sun J L C，Shupe L S，et a1. Supression of Wind-induced Instabilities using Nutation Dampers[C]// Proc Indian Acad Sci Ser Eng Sci, V 4 PT4, 461-470, Dec 1981.

[3] 周福霖.工程结构减震控制[M].北京:地震出版社，1997.

[4] 李宏男，霍林生.结构多维减震控制[M].北京：科学出版社，2008.

[5] Fujino Yozo , Pacheco Benito M, Chaiseri Piyawat，et al.Parametric Studies on TLD using circular container by free-oscillation experiments[C]// Doboku Gakkai Rombun-Hokokushu. Proceedings of the Japan Society of Civil Engineers，n 398 1-10, 177-187, Oct 1988.

[6] 欧进萍.结构控制振动[M].北京：科学出版社，2003.

[7] Huang Dong-yang, Tan Ping, Dai Na-xin, et al.Dynamic analysis on TLCMD[J].Science Technology and Engineering，2008,8(3):694-699.

[8] Saikai F, Takada S, Tamaki T.Tuned liquid column damper—new type device for suppression of building vibration[C]∥Proc.International Conference on High Rise Buildings, Nanjing, China, 1989:926-931.

[9] Yalla SK, Kareem A.Optimum absorber parameters for tuned liquid column damper[J].Journal of Structural Engineering, ASCE，2000，126(8)：906-915.

[10]Gao H, Kwok K C S, Samali B.Optimization of tuned liquid column dampers[J].Engineering Structures，1997，19(6)：476-486.