成品油管网运行优化
2011-01-22梁永图刘增哲
梁永图,刘增哲
(1.中国石油大学 石油工程学院,北京 102249;2.中国石油 北京油气调控中心,北京 100007)
成品油管网运行优化
梁永图1,刘增哲2
(1.中国石油大学 石油工程学院,北京 102249;2.中国石油 北京油气调控中心,北京 100007)
针对我国成品油管网的特点,以管网运行周期内的能耗费用最小为目标函数,考虑管网中各站场的进、出站压力约束、管网高低点压力约束及管网运行时的能量平衡约束等建立成品油管网优化运行的数学模型,并采用分阶段动态规划方法求解模型,得出管网系统在输送周期内各时段的优化配泵方案。将模型应用于某成品油管网,并将优化模拟计算结果与穷举法的计算结果进行对比分析。结果表明,优化模型可以得到令人满意的配泵方案,且计算效率更高,可以较好地应用于工程实践。
顺序输送;管网;数学模型;动态规划;优化运行
目前我国的成品油管道已经初步形成网络。已经建成的成品油长输管道有兰成渝成品油管道、西部成品油管道、港枣成品油管道、兰郑长成品油管道等。另外,我国拟建的东北地区成品油管道、抚郑成品油管道等必将使我国成品油管道连成网络[1-2]。为保证管网安全、经济地运行,有必要对成品油管网的优化运行进行研究。成品油管道顺序输送运行优化是在对管网系统进行分析的基础上,根据优化目标建立符合管网特点的优化运行数学模型,提出有效的求解方法。笔者以管网运行周期内的能耗费用最小为目标函数,考虑管网中各站场的进、出站压力约束、管网运行时的能量平衡约束以及管网高低点压力约束等建立成品油管网优化运行的数学模型并采用分阶段动态规划方法求解模型,得出管网系统在输送周期内各时段的优化配泵方案。
1 优化模型的建立
以树枝状成品油管网作为研究对象,研究的管网结构和计算管段划分如图1所示。以树枝状管网每一个树杈所在的点作为分界点,对整个管网进行计算管段的划分。从管道首站到第一个分界点间的管段为管段1,第一个分界点到第二个分界点间的管段为管段2,第一个分界点到支线油库2间的管段为管段3,以此类推其他管段。出于模型求解的需要,以干线上支线起点作为分界点划分计算阶段,干线首站至第一个分界点间管网为第一阶段,第一个分界点至第二个分界点间管网为第二阶段,其余以此类推。
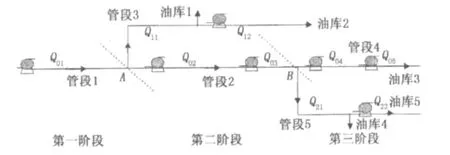
图1 成品油管网优化计算管段划分示意图Fig.1 Pipeline segment partition diagram for optimal calculation of products pipeline network
以管网输送周期内的能耗费用最小为目标,考虑管网中各站场的进、出站压力约束、管网运行时的能量平衡约束以及管网高低点压力约束等建立了成品油管网优化运行的数学模型,以求解管道系统在输送周期内的最优开泵方案[3-6]。模型为

式中,f为最小总能耗费用,元;dt为时间微元,s;μijk为第i管段第j泵站第k台泵的开关状态,μijk=1表示泵运行,μijk=0表示泵停运,有调速电机则0<μijk<1;n为管网管段个数;ni为第i管段的泵站个数;kij为第i管段第j泵站泵的台数;Qij为通过第i管段第j泵站的流量,m3/s;ρij为计算时刻过第i管段第j泵站的油品密度,kg/m3;Cij为第i管段j泵站的电价,元 /(kW·h);ηij为第i管段j泵站工作效率;ηijk为第i管段第j泵站第k台泵工作效率;m为流态指数;g为重力加速度,m/s2;aijk-为第i管段第j泵站第k台泵的扬程,m;T为模拟输送周期,s;为第i管段末端剩余压力,Pa;为第i管段的起点压力,Pa;pfi为第 i管段的沿程摩阻,Pa;pξi为第i管段的局部摩阻,Pa;Δpi为第i管段的高程差损失,Pa;为第 i管段末端最小压力,Pa;为计算时刻第m种油品在第i管段第hpi个高点处的压力,Pa;为第m种油品在第i管段第hpi个高点处管输条件下的饱和蒸汽压,Pa;Pi,lpj为计算时刻第i管段第 lpj低点处压力,Pa;为第 i管段第 lpj低点处的最大承受压力,Pa;和分别为第 i管段 j站出站压力和进站压力,Pa;为第i管段j泵站油流进站的最小压力,Pa;为第i管段j泵站油流出站的最大压力,Pa。
2 模型的求解
管道输送是使能量供应与消耗相平衡,理想的状态是管道的能量供应等于管道能量消耗,优化的目的是使管道的供能最大限度地接近运行的能量需求,以节省不必要的能耗[7-11]。以各管段起点的最低压力作为初始条件,既满足了泵站运行的进站压力要求也可以使各阶段计算出的初始供能方案更能接近该阶段的能量需求。然后利用分阶段动态规划进行求解,即先利用动态规划方法分别求解各阶段最初的配泵方案,继而以各阶段整体作为新动态规划一个阶段求解全局最优配泵方案,从第一阶段开始,以前一阶段余压作为下一阶段进管段压力,判断下一阶段初始配泵方案是否最优,如果不是最优则利用动态规划方法,以前一阶段余压作为初始条件对该阶段进行重新配泵,依此类推得到整个管网的优化配泵方案。
以图1所示管网为研究对象,引入输出权重做为泵站供能的调速因子,输出权重指泵站的实际输出压力和泵站的最高输出压力的比,输出权重在0~1取值,泵站的供能等于输出权重乘以泵站的最大供能。设各管段各泵站的最高输出压力为Hij米油柱(考虑了单台泵机组效率),输出权重为xij,i=1,…,n,j=1,…,ni,则全系统泵站因能量输出产生的电费总和W(X)为所以全线泵站的费用总和函数W(X)在区域内没有驻点,则W(X)在区域内沿每一条能量变化曲线是单调递增的。

设全线输油的费用最低需求为W0,则在满足能量需求的配泵方案中供能越是靠近W0,其配泵方案越优。
因此,对建立的管网数学模型采用以下求解过程(以图1为例):
(1)根据水力计算确定A、B点的最低压力,对于管段内的并联泵站,根据通过该泵站的流量、泵特性及该站最低出站压力确定需要运行的泵机组数。如果需要运行的泵机组数大于1,则把该并联泵站看成一个单泵运行的泵站,以并联运行泵机组的特性作为该泵的运行特性,以各管段均以最小压力进管段为初始条件,用已建立的数学模型对各阶段分别用动态规划求解最初的配泵方案。

3 模型的验证与应用
为了验证模型的正确性,以AB成品油管网为例对不同工况下的配泵方案进行建模求解,并对模型求解得到的结果和穷举法得到的结果进行对比。
某成品油管网始自山东A石化公司,终点设在安徽省B油库,管线系统总长765.1 km,其管道概况如图2所示。AB成品油管道干线有4座泵站,AB1和AB2支线在支线入口处各有3台泵机组[12]。

图2 AB管网概况示意图Fig.2 Diagram of AB pipeline network
管道干线和支线中充满90#汽油,各站进出站流量如表1所示。

表1 管道干线和支线各站进出站流量Table 1 Flow rate in/out of stations in trunk and branch lines of pipeline
进行优化配泵所得的配泵结果如表2所示。
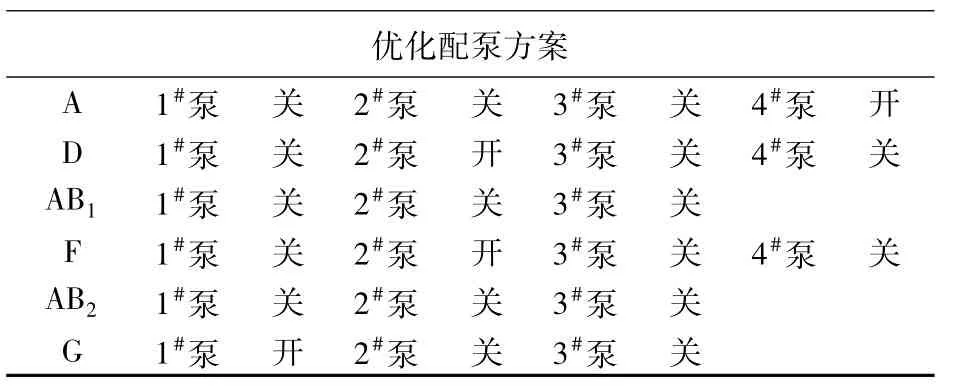
表2 优化配泵结果Table 2 Optimal pump configuration results
该算例是该输量和分输注入工况下管道运行能量需求最小的工况。能满足管道安全运行的配泵方案比较多,从节能降耗的角度来看,本文提供的优化运行算法所得的配泵方案和穷举法所得的最优配泵方案完全相同,能够起到优化运行的目的。该优化运行算法的运算循环次数只有296次,而穷举算法的运算循环次数高达221次,说明新算法在满足低能耗配泵的同时极大地提高了计算速度。
4 结束语
通过分阶段动态规划法对模型的求解,得出管网系统在输送周期内各稳定工况时段最优的配泵方案,极大地提高了运算速度。以AB成品油管道为例,对采用优化算法所得结果和穷举法所得结果进行了对比,说明了优化模型的正确性和有效性。
[1]朱喜龙.我国油气管道发展的探讨[J].炼油与化工,2005,16(2):4-9.
ZHU Xi-long.Disscusion on the development of oil and gas pipelines in our country [J].Refining and Chemicals,2005,16(2):4-9.
[2]王宝群,林燕红,代运铎.我国成品油管道现状及展望[J].石油规划设计,2010,21(5):7-9.
WANG Bao-qun,LIN Yan-hong,DAI Yun-duo.Present status and prospect of product pipelines in China[J].Petroleum Planning & Engineering,2010,21(5):7-9.
[3]DIEGO C Cafaro,JAIME Cerdá.Optimal scheduling of multiproduct pipeline systems using a non-discrete MILP formulation[J].Computers & Chemical Engineering,2004,28(10):2053-2068.
[4]ANDREW E Boyd,RIDGEAY L Scott,WU Su-ming.E-valuation the quality of pipeline operation algorithms[C].PSIG 29th Annual Meeting,1997.
[5]MIRHASSANI S A,GHORBANALIZADEH M.The multi-product pipeline scheduling system [J].Computers and Mathematics with Applications,2008,56(4):891-897.
[6]CLAUDIO Veloso Barreto,LIUIS fernado Goncalves Pires,LIUIS Fernando Alzuguir Azevedo.Optimization of pump energy consumption in oil pipelines[C].International Pipeline Conference,2004.
[7]梁永图,宫敬,康正凌,等.成品油管道优化运行研究[J].石油大学学报:自然科学版,2004,28(4):97-101.
LIANG Yong-tu,GONG Jing,KANG Zheng-ling,et al.Optimal operation of multi-product pipeline [J].Journal of the University of Petroleum,China(Edition of Natural Science),2004,28(4):97-101.
[8]宫敬,储祥萍,于达.成品油管道优化运行方法研究[J].油气储运,2000,19(10):22-25.
GONG Jing,CHU Xiang-ping,YU Da.Study of multiproduct pipeline optimum operating method[J].Oil&Gas Storage and Transportation,2000,19(10):22-25.
[9]蒋仕章,蒲家宁.格拉管道顺序输送运行优化研究[J].管道技术与设备,2005(4):1-2,6.
JIANG Shi-zhang,PU Jia-ning.Study of the operational optimization of batch transportation in Golmud-Lhasa pipeline[J].Pipeline Technique and Equipment,2005(4):1-2,6.
[10]梁永图.成品油管道顺序输送运行优化研究[D].北京:中国石油大学石油工程学院,2001.
LIANG Yong-tu.Study of optimal operation for products pipeline[D].Beijing:College of Petroleum Engineering in the University of Petroleum,China,2001.
[11]孟振虎.输油管道运行优化理论与方法的分析[J].天然气与石油,2004,22(1):18-22.
MENG Zhen-hu.Analysis on theory and method of optimum operation of oil pipeline technique and equipment[J].Natural Gas and Oil,2004,22(1):18-22.
[12]付永杰.鲁皖成品油管道混油优化运行及处理分析[J].管道技术与设备,2007(5):6-8.
FU Yong-jie.Analysis of the mixed oil optimal operation and treatment in Luwan product oil pipeline [J].Pipeline Technique and Equipment,2007(5):6-8.
Optimal operation of multi-product pipeline network
LIANG Yong-tu1,LIU Zeng-zhe2
(1.College of Petroleum Engineering in China University of Petroleum,Beijing 102249,China;2.PetroChina Oil& Gas Pipeline Control Center,Beijing 100007,China)
After studying features of multi-product pipeline network,using the minimum energy cost as the objective function,an optimal mathematical model was established considering pressures and flow rate restraints,operation restraints of different pump stations and energy balance of pipeline network.The model was solved using dynamic programming algorithm.The optimal pump configuration was provided by the model.Then the optimal mathematical model was applied to some products pipeline network to demonstrate its feasibility.The results by the optimal model were compared with those of exhaustive method.The results show that the model could draw out the optimal pump configuration and work efficiently in pipeline transportation engineering.
batch transportation;pipeline network;mathematical model;dynamic programming;optimal operation
TE 832.2
A
10.3969/j.issn.1673-5005.2011.03.023
1673-5005(2011)03-0115-04
2010-10-09
梁永图(1971-),男(汉族),河北怀安人,副教授,博士,主要从事油气长距离输送技术研究。
(编辑 沈玉英)
