两类特殊本原不可幂定号有向图基的界

王慧敏,邵燕灵

(中北大学数学系,山西太原030051)

两类特殊本原不可幂定号有向图基的界

王慧敏,邵燕灵

(中北大学数学系,山西太原030051)

为了进一步了解本原不可幂定号有向图基的相关性质,对两类含有四个圈的本原不可幂定号有向图的基进行了研究.利用有关本原不可幂定号有向图的引理及定义,并分析有向图的性质,综合运用指数、SSSD途径对和图的直径分别求其上、下界,从而得到了两类有向图基的界.若上界与下界相等,则可得到其基的具体值.

不可幂;本原指数;基;定号有向图;SSSD途径对

1 引 言

有关定号有向图基的研究,目前取得了一些结果.文献 [2]中讨论了本原不可幂定号对称有向图(含自环)的基;文献 [3]中作者介绍了可约符号模式矩阵周期与基;文献 [4]中作者介绍了不可约广义符号模式矩阵基的界;文献 [5]中给出了几乎可约符号模式矩阵基的界.下面是有关基的一些定义.

设A=(aij)是一个n阶符号模式矩阵,A的伴随有向图D(A) (可能含有环)是指一个有向图,它包含点集V={1,2,…n}和弧集 E={(i,j)|aij≠0}.按照A中aij的符号,将D(A)中的每一条弧定义一个符号1或-1所得的图称为D(A)的定号有向图,记为S(A),S(A)为A的伴随定号有向图,即D(A)就成为S(A)的基础有向图.

设S为一个定号有向图,S中的一条途径W是一个有关弧的序列:e1,e2,…,ek,使得ei的终点与ei+1的起点相同,其中i=1,2,…,k-1.所含弧的条数 k即是途径W的长度,记为l(W).途径W的符号被定义为 记为sgn(W).如果一个定号有向图中的两条途径W1和W2有相同的起点和相同的终点及相同的长度,但是符号相反,则称它们为一个SSSD途径对[1].

定义1.1 设D为有向图,如果存在正整数l,使得对于D的任意顶点νi,νj(可以相同),在D中都存在从νi到νj长为l的途径,则称 D为本原有向图.上述最小的 l称为D的本原指数,记为exp(D).

定义1.2 设 D是一个本原有向图,νi∈V(D),存在正整数 p,若对任意的 t≥p,从顶点νi到D中的任一点都有长为t的途径,满足上述条件的最小正整数 p,就叫做顶点νi的点指数,记为expD(νi).

定义1.3 设 S是一个本原不可幂定号有向图,若对任意顶点νi和νj(可以相同),并且对任意 t≥l,从νi到νj都有长为t的SSSD途径,则称满足上述条件的最小正整数 l,就叫做 S的基,记为 l(S).

定义1.4[1]如果定号有向图S中不包含SSSD途径对,则称S为可幂的,否则称S为不可幂的.

定义1.5 设S是一个本原不可幂定号有向图,S的歧义指数 (ambiguous index)被定义为S中最短的SSSD途径对的长度,记为 r(S).用 ru,ν表示从顶点u到顶点ν的最短的SSSD途径对的长度.

2 预备知识

引理2.1[5]设S是一个本原定号有向图,则 S不可幂当且仅当S中存在两个不同的圈C1,C2(其长分别为 p1和 p2)满足下面两个条件之一:

(Ⅰ)p1是奇数,p2是偶数,并且有sgnC2=-1;

(Ⅱ)p1和 p2都是奇数,并且有sgnC1=-sgnC2.

为了方便,称满足 (Ⅰ)或 (Ⅱ)的圈对 C1和 C2为“异圈对”.容易看到若 C1和 C2是长分别为 p1和 p2的异圈对,则闭圈对W1=p2C1和W2=p1C2有相同的长度 p1p2,但有不同的符号:

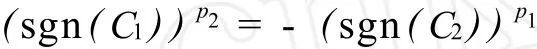
设 a1,…,ak都为正整数.Frobenius集S(a1,…,ak)定义如下:

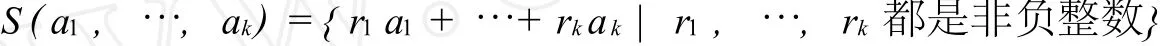
根据Schur引理,如果 g.c.d(a1,…,ak)=1,那么S(a1,…,ak)包括足够大的正整数.在这种情况下,使得所有 m≥φ的整数m∈S(a1,…,ak)的最小整数φ,称为Frobenius数φ(a1,…,ak).

根据上面的定义,则有φ(a1,…,ak)-1∉S(a1,…,ak).如果 a,b是互素的两个正整数,则有

设R={l1,…,lk}是本原有向图D中圈长的集合,且 g.c.d(l1,…,lk)=1.对于 D中的每个顶点x和顶点y,用 d(x,y)表示从 x到y的距离,dR(x,y)表示从 x到y接触R中每一长度的圈的最小距离.用φR=φ(l1,…lk)表示Frobenius数,则对于本原指数和点指数有以下式子成立:

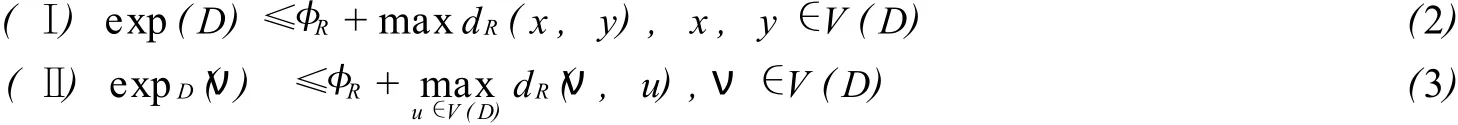
引理2.2[5]设S是一个n阶本原不可幂定号有向图,其基础图为 D.d(S)表示 S的直径,W1和W2为从顶点 u到顶点ν的长度为ru,ν的SSSD途径对.则

本文主要是对基础图是D1、D2的本原不可幂定号有向图 S1、S2进行研究,得到了不同情况下有向图的基或基的界.

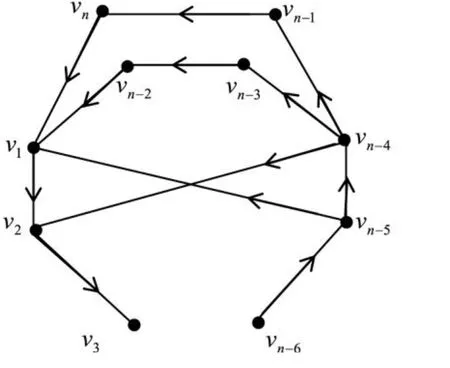
图1 定号有向图 S1的基础图 D1

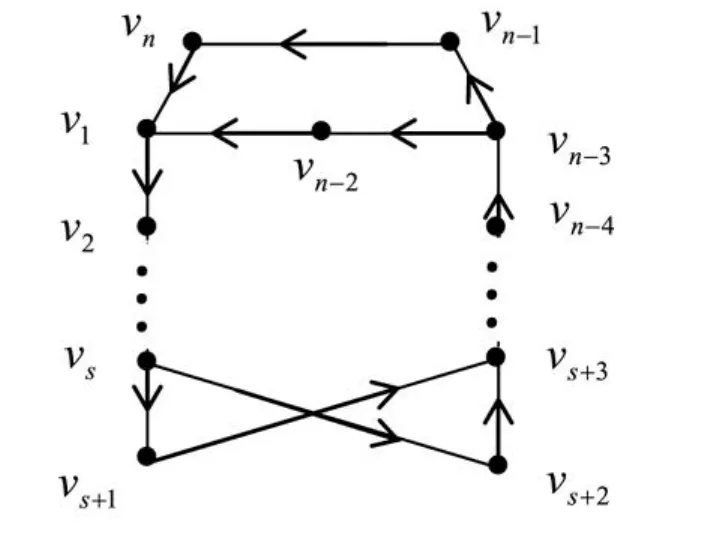
图2 定号有向图 S2的基础图 D2

3 结 论

定理3.1 设 S1是 n(nφ8,n≠8+3x)(其中 x为正整数)阶本原不可幂定号有向图,D1是它的基础图,则

(Ⅰ)如果 S1中的两个 n-2圈具有不同的符号,则 l(S1)≤n2-7n+17.

(Ⅱ)如果S1中的两个n-5圈具有不同的符号,则l(S1)=n2-7n+12.

(Ⅲ)如果S1中的两个n-2圈具有相同的符号,且两个n-5圈也具有相同的符号,则l(S1)=2n2-15n+27.

证明 在图S1中,记 R={n-5,n-2},且 d(S1) =n-1.

(Ⅰ) 令 Q1=(νn-4,νn-3)+(νn-3,νn-2)+(νn-2,ν1) 和 Q2=(νn-4,νn-1)+(νn-1,νn)+(νn,ν1) 是从νn-4到ν1的长为3的两条路径.由于 S1中的 (仅有的)两个 n-2圈具有不同的符号,则一定有sgnQ1=-sgnQ2, 故 rνn-4,ν1≤3, 又u)≤n-3,由公式 (1) 和 (3) 得

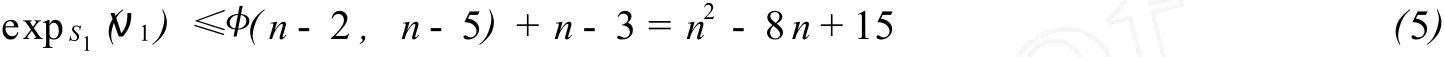
再由公式 (4)得

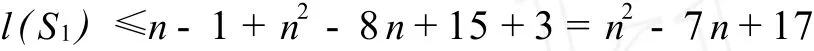
即定理3.1的 (Ⅰ)得证.

(Ⅱ) 令 Q1=(νn-5,ν1)+(ν1,ν2) 和 Q2=(νn-5,νn-4)+(νn-4,ν2) 是从νn-5到ν2的长为 2 的两条路径.由于 S1中的 (仅有的)两个 n-5圈具有不同的符号,则一定有sgnQ1=-sgnQ2,故又由于≤n-4,由公式 (1) 和 (3) 得

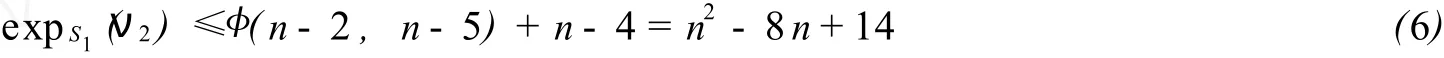
对任意的νi,νj∈V(D),从νi到νn-5的路径的长度 d≤n-4.又由于ν2在两个 Cn-5上,可知对任意的 t≥n2-8n+14,存在从ν2到νj的一条t长途径,那么就存在一对从νi到νj的长度为d+2+n2-8n+14+n-4-d=n2-7n+12的SSSD途径对.所以可得

接下来证明l(S1)≥n2-7n+12.用反证法,证明从νn-1到νn无长为k=n2-7n+11的SSSD途径对.

设W1和W2是任意两条从νn-1到νn的长为k的途径,那么每个Wi(i=1,2)是由从νn-1到νn长为1的路径和若干个 (至少一个)Cn-2圈和Cn-5圈组成 (其中Cn-2,Cn-5分别表示长度为n-2和n-5的圈).即 k=l(Wi)=n2-7n+11=ai(n-2)+bi(n-5)+1+n-2(ai≥0,bi≥0),就有 (ai+1) (n-2)=(n-2-bi)(n-5).可知要使等式成立,一定有bi=n-2,0.由于bi=n-2时,ai=-1与 ai≥0矛盾,故bi=0成立,此时 ai=n-6.即两个任意从νn-1到νn的长为k的途径都只绕Cn-2,不绕 Cn-5,则 sgn(W1)=sgn(W2).所以S1中不存在长为k的SSSD途径对,从以上讨论中可得

综合 (7)和 (8),得l(S1)=n2-7n+12.即定理3.1的 (Ⅱ)得证.

(Ⅲ)在图 S1中,如果S1中的 (仅有的)两个 n-2圈具有相同的符号,且 (仅有的)两个 n-5圈也具有相同的符号,则sgnQ1=sgnQ2.由于图S1是本原不可幂的,且图S1中仅有两个n-2圈和两个 n-5圈,由引理2.1知:每一个 n-2圈与一个 n-5圈都可以构成一对“异圈对”.所以 (n-2)Cn-5和(n-5)Cn-2有不同的符号 (其中 Cn-2表示由 (νn-4,νn-3,νn-2, …,νn-5)组成的 n-2圈,Cn-5表示由(Vn-4,ν2, …νn-6,νn-5) 组成的 n-5 圈). 令 P1=(νn-4,νn-3)+(νn-3,νn-2)+(νn-2,ν1)+(ν1,ν2)和 P2=(νn-4,ν2) 分别是从νn-4到ν2的长为 4 和 1 的两条路径. P=(ν2,ν3)+ …+(νn-6,νn-5)+(νn-5,νn-4)是从ν2到νn-4的唯一路径.再令W1=P1+(n-6) Cn-2,W2=P2+(n-3)Cn-5是从νn-4到ν2的长为 n2-8n+16的途径对,那么就有W1+P=(n-5)Cn-2,W2+P=(n-2)Cn-5.因 (n-5)Cn-2和 (n-2)Cn-5有不同的符号,故 W1与 W2也有不同的符号,从而 W1与W2为一对从νn-4到ν2长为 n2-8n+16的SSSD途径对,所以 rνn-4,ν2≤n2-8n+16. 对任意的νi,νj∈V(D),从νi到νn-4的路径的长度 d≤n-3.又由于ν2是所有圈的公共点,再由 (6)可知,对任意的 t≥n2-8n+14存在从ν2到νj的一条t长途径.那么就存在一对从νi到νj的长度为d+n2-8n+16+n2-8n+14+n-3-d=2n2-15n+27的 SSSD途径对.所以可得

接下来证明l(S1)≥2n2-15n+27.用反证法,证明从νn-1到νn无长为k=2n2-15n+26的 SSSD途径对.

设W1和Ww是任意两条从νn-1到νn的长为k的途径,那么每个Wi(i=1,2)是由从νn-1到νn长为1的路径和若干个 (至少一个)Cn-2圈和若干个 Cn-5圈组成.即 k=l(Wi)=ai(n-2)+bi(n-5)+1(ai≥1,bi≥0),故有:(a2-a1)(n-2)=(b1-b2)(n-5).设b1-b2=(n-2)x,那么 a2-a1=(n-5)x.下面证明 x=0,用反证法:如果 x≥1,则 a2≥a1+n-5≥n-4(由于 a1≥1),所以 k=[a2-(n-4)](n-2)+b2(n-5)+1+(n-4)(n-2).则有 φ(n-2,n-5)-1=(n-3)(n-6)-1=k-[1+(n-4)(n-2)]=[a2-(n-4)](n-2)+b2(n-5)∈S(n-2,n-5)与Frobenius数φ(n-2,n-5)的定义矛盾.同理可证 x≤-1也与Frobenius数φ(n-2,n-5)的定义矛盾.所以 x=0成立,即有a1=a2,b1=b2.那么sgnQ1=sgnQ2,所以S1中不存在长为k的SSSD途径对.从以上讨论证明中可得到

综合 (9)和 (10),得l(S1)=2n2-15n+27.定理3.1得证.

定理3.2 设 S2是 n(s≥2,n≥s+5)(其中s为正整数)阶本原不可幂定号有向图,D2是它的基础图,则

(Ⅰ)如果S2中的两个n-2圈具有不同的符号,则l(S2)=n2-5n+8

(Ⅱ)如果S2中的两个n-3圈具有不同的符号,则l(S2)=n2-5n+6

(Ⅲ)如果S2中的两个n-2圈具有相同的符号,且两个n-3圈也具有相同的符号,则l(S2)=2n2-11n+17.

证明 在图S2中,记 R={n-2,n-3},且 d(S2)=n-2.

(Ⅰ) 令 Q1=(νs,νs+1)+(νs+1,νs+3) 和 Q2=(νs,νs+2)+(νs+2,νs+3) 是从νs到νs+3的长为 2 的两条路径.由于 S2中的 (仅有的)两个 n-2圈具有不同的符号,则一定有 sgnQ1=-sgnQ2,故 rνs,νs+3≤2,u)≤n-4,由公式 (1) 和 (3) 得

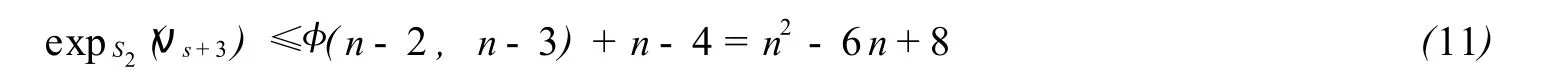
再由公式 (4)得

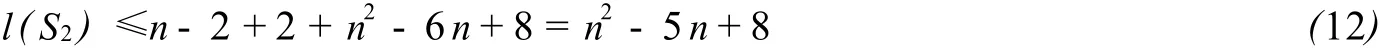
接下来证明l(S2)≥n2-5n+8.用反证法,证明从νn-1到νn无长为k=n2-5n+7的 SSSD途径对.

设W1和W2是任意两条从νn-1到νn的长为k的途径,那么每个Wi(i=1,2)是由从νn-1到νn长为1的路径和若干个 (至少一个)Cn-2圈和Cn-3圈组成 (其中Cn-2,Cn-3分别表示长度为n-2和n-3的圈).即 k=l(Wi)=n2-5n+7=ai(n-2)+bi(n-3)+1+n-2(ai≥0,bi≥0),就有 (ai+1)(n-2)=(n-2-bi)(n-3).可知要使等式成立,一定有bi=n-2,0.由于bi=n-2时,ai=-1与 ai≥0矛盾,故bi=0成立,此时 ai=n-4.即两个任意从νn-1到νn的长为k的途径都只绕Cn-2,不绕 Cn-3,则sgn(W1)=sgn(W2).所以S2中不存在长为k的SSSD途径对,从以上讨论中可得

综合 (12)和 (13),得l(S2)=n2-5n+8.即定理3.2的 (1)得证.

(Ⅱ)由于S2中的 (仅有的)两个n-3圈具有不同的符号,则一定有sgnQ1=-sgnQ2,由于在同一个图中且有相同的路径,可得 (11).对任意的νi,νj∈V(D),从νi到νs的路径的长度d≤n-4.又由于νs+3在两个 Cn-3上,可知对任意的t≥n2-6n+8,存在从νs+3到νj的一条t长途径,那么就存在一对从νi到νj的长度为d+2+n2-6n+8+n-4-d=n2-5n+6的SSSD途径对.所以可得

接下来证明l(S2)≥n2-5n+6.用反证法,证明从νn-2到νn-2无长为 k=n2-5n+5的 SSSD途径对.

设W1和W2是任意两条从νn-2到νn-2的长为 k的途径,那么每个Wi(i=1,2)是由若干个 Cn-2圈和Cn-3圈 (至少一个)组成.即 k=l(Wi)=n2-5n+5=ai(n-2)+bi(n-3)+n-3(ai≥0,bi≥0),就有(ai+1)(n-2)=(n-2-bi)(n-3).以下同定理3.2(1)的证明,所以可得

综合 (14)和 (15),得l(S2)=n2-5n+6.即定理3.2的 (2)得证.

(Ⅲ)在 S2中,如果 S2中的 (仅有的)两个 n-2圈具有相同的符号,且 (仅有的)两个 n-3圈也具有相同的符号,则sgnQ1=sgnQ2.由于S2是本原不可幂的,且S2中仅有两个n-2圈和两个n-3圈,由引理2.1知:每一个n-2圈与一个 n-3圈都可以构成一对“异圈对”.所以 (n-2)Cn-3和 (n-3)Cn-2有不同的符号 (其中 Cn-2表示由 (ν1,ν2, …,νs,νs+1,νs+3, …,νn-3,νn-1,νn) 组成的 n-2圈,Cn-3表示由 (ν1,ν2, …,νs,νs+1,νs+3, …,νn-3,νn-2组成的 n-3圈).

令 P1=(νn-3,νn-1)+(νn-1,νn)+(νn,ν1) 和 P2=(νn-3,νn-2)+(νn-2,ν1) 分别是从νn-3到ν1的长为 3 和 2 的两条路径. P=(ν1,ν2)+ …+(νs,νs+1)+(νs+1,νs+3)+ …+(νn-4,νn-3) 是从ν1到νn-3的唯一路径.再令W1=P1+(n-4)Cn-2,W2=P2+(n-3)Cn-3是从νn-3到ν1的长为 n2-6n+11的途径对,那么就有W1+P=(n-3)Cn-2,W2+P=(n-2)Cn-3.因 (n-3)Cn-2和 (n-2)Cn-3有不同的符号,故W1与W2也有不同的符号,从而W1与W2为一对从νn-3到ν1长为 n2-6n+11的 SSSD途径对,所以rνn-3,ν1≤n2-6n+11. 又2≤n-3,由公式 (1) 和 (3) 得

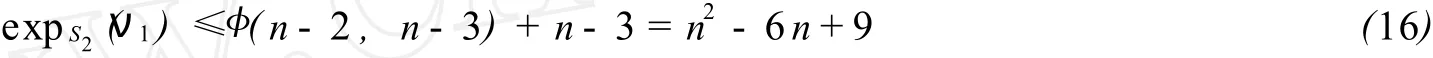
对任意的νi,νj∈V(D),从νi到νn-3的路径的长度 d≤n-3.又由于ν1是所有圈的公共点,再由(16)可知,对任意的t≥n2-6n+9存在从ν1到νj的一条t长途径.那么就存在一对从νi到νj的长度为d+n2-6n+11+n2-6n+9+n-3-d=2n2-11n+17的SSSD途径对.所以可得

接下来证明l(S2)≥2n2-11n+17.用反证法,证明从νn-1到νn无长为k=2n2-11n+16的 SSSD途径对.

设W1和W2是任意两条从νn-1到νn的长为k的途径,那么每个Wi(i=1,2)是由从νn-1到νn长为1的路径和若干个 (至少一个)Cn-2圈和若干个 Cn-3圈组成.即 k=l(Wi)=ai(n-2)+bi(n-3)+1(ai≥1,bi≥0),故有:(a2-a1)(n-2)=(b1-b2)(n-3).设 b1-b2=(n-2) x,那么 a2-a1=(n-3) x.下面证明 x=0,用反证法:如果 x≥1,则 a2≥a1+n-3≥n-2(由于 a1≥1),所以 k=[a2-(n-2)](n-2)+b2(n-3)+1+(n-2)2.则有 φ(n-2,n-3)-1=(n-3)(n-4)-1=k-[1+(n-2)2=[a2-(n-2)](n-2)+b2(n-3)∈S(n-2,n-3)与Frobenius数φ(n-2,n-3)的定义矛盾.同理可证 x≤-1也与Frobenius数φ(n-2,n-3)的定义矛盾.所以 x=0成立,即有 a1=a2,b1=b2.那么sgnQ1=sgnQ2,所以S1中不存在长为k的SSSD途径对.从以上讨论证明中可得到

综合 (17)和 (18),得l(S2)=2n2-11n+17.定理3.2得证.

[1] Gao YB,Huang YH,Shao YL.Bases of primitive non-powerful singed symmetric digraphs with loops[J].Ars Combin,2009,90：383-388

[2] Li Z,Hall F,Stuart L.Irreducible powerful ray pattern matrices[J].Linear Algebra Appl,2002,342：47-58

[3] Liu BB.The period and base of a reducible sign pattern matrix[J].Discr Math,2007,307：3031-3039

[4] Gao YB,Shao YL.Generalized exponents of primitive two-colored digraphs[J].Linear Algebra Appl,2009,430：1550-1565

[5] Lundgren JR,Maybee JS.Some properties of a class of recursively defined digraphs[J].Syst Sci,1991,16(1)：29-36

[6] Wang LQ,Miao ZK,Yan C.Local bases of primitive non-powerful signed digraphs[J].Discr Math,2009,309：748-754

[7] Liu BL,You L H.Bounds on the base of primitive nearly reducible sign pattern matrices[J].Linear Algebra Appl,2006,418：863-881

[8] Gao YB,Shao YL,Shen J.Bounds on the local bases of primitive non-powerful nearly reducible sign patterns[J].Linear Multil Algebra,2009,57(2)：205-215

[9] Ma HP.Bounds on the local bases of primitive non-powerful minimally strong signed digraphs[J].Linear Algebra Appl,2009,430：718-731

[10] You L H,Shao J Y,Shan HY.Bounds on the bases of irreducible generalized sign pattern matrices[J].Linear Algebra Appl,2007,427：285-300

Bounds on Bases of Two Special Classes of Primitive Non-powerful Signed Digraphs

WANG Hui-min,SHAO Yan-ling
(College of Science,North University of China,Taiyuan 030051,China)

The bases of two special classes of primitive non-powerful signed digraphs with four simple Coops were studied to research the related properties about primitive non-powerful signed digraphs.Through some lemmas and definition of the primitive non-powerful signed digraphs,and the analysis of the signed digraph,and using the knowledge of primitive exponent,SSSDwalks and the diameter of a digraph,we obtain the bounds on the bases of two special classes of signed digraphs.If the upper bounds are equal with the lower bounds,the specific value of the bases is obtained.

non-powerful;primitive exponent;bases;signed digraph;SSSDwalks

O 157.5

A

1673-1492(2011)04-0001-05

来稿日期：2011-05-10

国家自然科学基金资助项目 (11071227);山西省自然科学基金资助项目 (2008011009)

王慧敏(1986-),女,山西晋城人,中北大学数学系在读研究生.导师：邵燕灵 (1963-),女,教授,博士,博士生导师.

刘守义 英文编辑：刘彦哲]