椭球封头卧式储油罐的变位影响

林智燕，王 倩，薛茴文，李韶伟

（台州学院 数学与信息工程学院，浙江 临海 317000）

椭球封头卧式储油罐的变位影响

林智燕，王 倩，薛茴文，李韶伟＊

（台州学院 数学与信息工程学院，浙江 临海 317000）

探讨椭球封头卧式储油罐的纵向变位对罐容表的影响。本文分别建立了椭球封头卧式储油罐的无偏模型V=V0（H）和纵向偏转模型V=Vα（H），对比研究纵向变位参数α对椭球封头卧式储油罐的罐容表的影响。对于给定的一组椭球封头卧式储油罐数据和较小的纵向变位参数α，分析误差并证明了模型的可靠性。

卧式储油罐；罐容表；变位参数

1 引言

探讨纵向变位对罐容表的影响，假设椭球封头卧式储油罐为图1所示的规则几何体，忽略罐壁厚度、储油罐附属构建对罐内实际储油量计算的影响，忽略温度、气压等自然因素及油的挥发损耗等因素。

椭球封头卧式储油罐的主体部分为椭圆柱体（长度为L），左、右半椭球是椭球体（轴长为a，b，c）的对称两部分。如图1所示，以左半椭球的椭圆截面的中心为原点O，以经过原点O的椭圆柱体的母线方向为x轴，过原点O的竖直方向为y轴，垂直xoy平面向外的方向为z轴建立空间直角坐标系。

无偏转时，椭球封头卧式储油罐的储油量V与油位高度H的函数模型［1-3］V=V0（H）很容易得到。而当储油罐发生较小角度的纵向偏转α时，储油罐的罐容表读数不准确，需要对罐容表进行重新标定。本文将建立椭球封头卧式储油罐罐内实际储油量V与油位高度H及变位参数α之间的函数模型［4］，分析纵向变位导致的罐容表的误差。

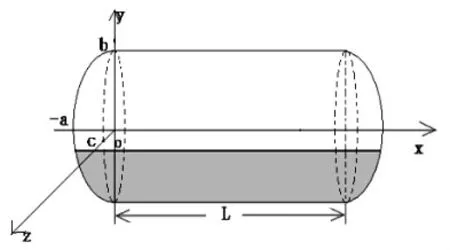
图1 无偏转储油罐的空间直角坐标系

2 建立模型

2.1 无偏模型

当椭球封头储油罐无纵向偏转时，如图1所示建立空间直角坐标系，则储油罐的储油量模型［2］为

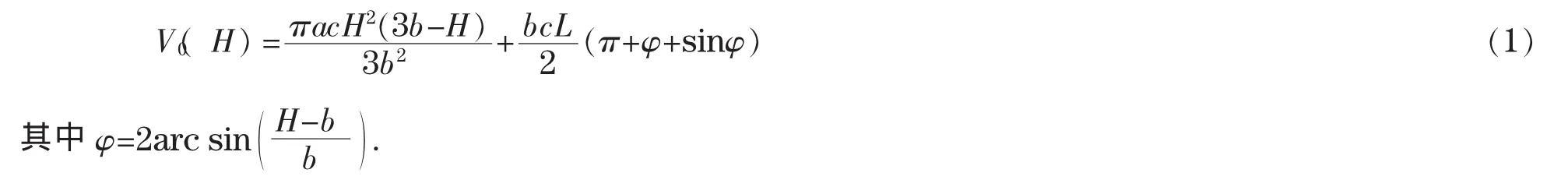
2.2 纵向变位模型

图2所示的是逆时针纵向偏转α后的椭球封头卧式储油罐。不同油位高度，椭球封头卧式储油罐的储油量的计算方式也不同，分5种情况讨论如下（设P=L1tanα+H-b）.

图2 纵向偏转α的储油罐示意图

图3 纵向偏转α时的截面示意图

2.2.1 当-L1tanα≤H＜（L-L1）tanα 时，油面介于 l0和 l1之间（见图 3）。

如图3所示，左半椭球的储油量为

2.2.2 当（L-L1）tanα≤H＜b-L1tanα 时，油面介于 l1和 l2之间（见图 3）.

左半椭球的储油量V1即为（2）式.

椭圆柱体的储油量为

类似于（2）式，右半椭球的储油量为

2.2.3 当 b-L1tanα≤H＜b+（L-L1）tanα 时，油面介于 l2和 l3之间（见图 3）。

左半椭球的储油量为

椭圆柱体和右半椭球的储油量V2和V3即分别为（4）式和（5）式.

2.2.4 当 b+（L-L1）tanα≤H＜2b-L1tanα 时，油面介于 l3和 l4之间（见图 3）。

左半椭球和椭圆柱体的储油量V′1和V2即为（6）式和（4）式.

右半椭球的储油量为

2.2.5 当 2b-L1tanα≤H≤2b+（L-L1）tanα 时，油面介于 l4和 l5之间（见图 3）。

左半椭球的储油量为

椭圆柱体的储油量为

右半椭球的储油量V′3即为（7）式。

综上，可将上述的5种情况归结为一个分段函数模型V=Vα（H），它精确刻画了纵向变位α之后罐容表V与油位高度H的函数关系。

2.3 模型求解

由于纵向变位α的存在，利用Maple软件计算（2）式-（9）式的积分颇为繁琐，需适当的近似简化，才能得到模型初等函数表达形式 V＝V（a，b，c，L，L1，H，α）。

在此，为了后续分析讨论的方便，本文给出参数a＝0.3，b=0.9，c=1.25，L=6，L1=2 的模 型求解 结果。 利用Maple软件可得到储油罐无偏转、储油罐纵向偏转α=2°和α=4°的储油量的函数图形（如图4所示）。

2.4 误差分析

图 4 无偏、α=2°和 α=4°的函数图形

如图4所示，当存在纵向偏转α时，储油罐的罐容表的偏差明显。考虑较小角度的纵向变位（α＜5°），对给定的参数 a＝0.3，b=0.9，c=1.25，L=6，L1=2，计算以下两类误差

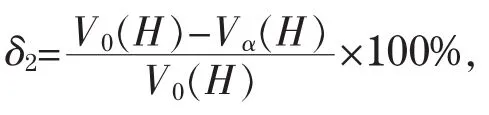
可得H-△V的绝对误差分析图5和相对误差分析图6如下

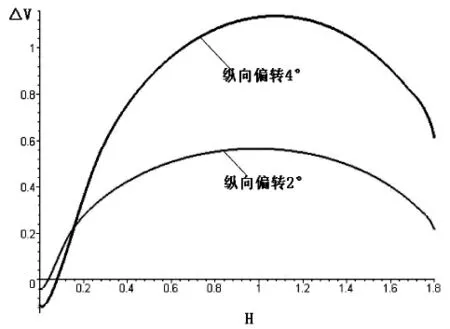
图5 绝对误差分析图

图6 相对误差分析图

在此，对应于α=2°，当H≈0.987时，绝对误差最大为δ1≈0.565；当 H≈0.108时，相对误差最大为δ2≈27.08%；对应于 α=4°，当 H≈1.074时，绝对误差最大为 δ1≈1.138；当 H≈0.219时，相对误差最大为δ2≈26.78%。

同理，可计算以下两类误差

可得V-△H的绝对误差分析图7和相对误差分析图8如下

图7 绝对误差分析图

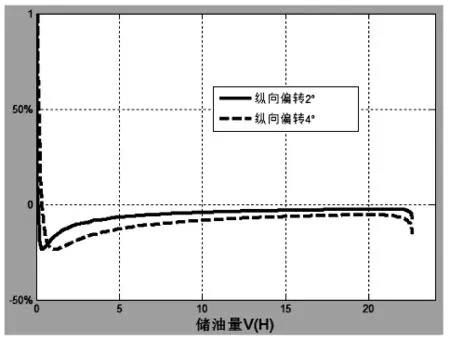
图8 相对误差分析图

从图7和图8上很容易看出，纵向变位对油面高度的影响，当储油量V很小或很大时，绝对误差较大；而当储油量V很小时，相对误差较大；

2.5 总结

综上所述，纵向变位α对储油罐罐容表的影响比较显著。当储油罐的储油量较小时，其相对误差变化明显，最大能超过25%，之后随着储油量的增加，其变化趋于平缓；当储油罐的油位高度达到和略超过储油罐高度的一半时，其绝对误差较大，最大能占到储油罐体积的5%。

总之，在实际的生产过程中需监测储油罐的纵向变位情况，及时修订罐容表，以减少罐容表的不准确而导致储油量的计算误差。

［1］刘奇央.卧式容器容积与液位的关系式［J］.黑龙江电力技术，1998，20（4）：215-217.

［2］田铁军.倾斜卧式罐直圆筒部分的容积计算［J］.现代计量测试，1999（5）：32-36.

［3］宁苗苗.液氨储存罐深度——容积函数的建立与应用［J］.高等函授学报，2010，23（1）：73-74.

［4］姜启源，谢金星，叶俊.数学模型（第三版）［M］.北京：高等教育出版社，2003：82.

［5］Maple 图形与动画［EB/OL］.http：//scumath2008.blog.163.com/blog/static/631500842008028103840738/

The Deflection Impact of the Ellipsoid Tank Head

LIN Zhi-yan，WANG Qian，XUE Hui-wen，LI Shao-wei*

(School of mathematics and information engineering， Taizhou University， 317000， Zhejiang)

This paper discussed the impact of the occurrence of ellipsoid tank head vertical deflection of the tank capacity table horizontal calibration. This paper established the no deflection model and the vertical deflection model of the horizontal storage tank and comparative studied the impact of the vertical deflection parameters on the horizontal ellipsoidal head tank of the tank capacity table. Under a given set of measured data of the occurrence of ellipsoid tank and the minor vertical deflection angles， the reliability of the model error is proved.

horizontal storage tank， vertical deflection， modification parameters

耿继祥）

TE972.1

A

1672-3708（2011）03-0003-04

2011-05-16

台州学院2011年校立学生科研项目（项目编号：11XS13）

李韶伟（1979- ），男，浙江仙居人，讲师，博士生，主要从事微分方程方面的研究。