一类非线性时滞系统的自适应动态面控制

王圣宇，吉 梗，朱琼瑶，李玲玲，王 赛

（台州学院 数学与信息工程学院，浙江 临海 317000）

一类非线性时滞系统的自适应动态面控制

王圣宇，吉 梗＊，朱琼瑶，李玲玲，王 赛

（台州学院 数学与信息工程学院，浙江 临海 317000）

针对一类严格反馈非线性时滞系统，提出了一种自适应神经网络动态面控制方案。通过引入一阶滤波器，避免了传统反演设计中的“计算膨胀”问题。通过构造恰当的Lyapunov-Krasovskii函数，对未知时滞项进行了补偿。此外，基于Lyapunov稳定性理论，证明了闭环系统所有信号半全局一致最终有界。最后，仿真实例表明了所提控制方案的有效性。

自适应控制；神经网络；动态面控制；非线性时滞系统

1 引言

在非线性系统设计中，模糊和神经网络是处理未知非线性函数常用的智能控制方法。在这些方法中，将模糊逻辑系统、神经网络系统和自适应反演法相结合，解决了许多不确定非线性系统的自适应控制器设计问题［1-3］。但是，基于反演技术的自适应控制方法都有一个缺陷，即“计算膨胀”问题。由于每一步递推设计中都要对虚拟控制律进行重复求导，导致虚拟控制量所含项随系统阶数的增加而爆炸性膨胀，使得控制器的计算量非常大。针对反演法中的计算膨胀问题，Swaroop等在文献［4］中首次提出了动态面控制方法，通过引入一阶低通滤波器，消除了对虚拟控制律的求导，使得计算量大大降低。随后，Wang等［5］将动态面技术与神经网络控制相结合，针对一类严格反馈非线性系统，提出了自适应动态面控制方法。此后许多学者对动态面技术的自适应控制作了更进一步的研究［6-9，12］。然而基于动态面控制方法的非线性系统控制中，还存在在线调整参数过多的现象，这样将加大计算负担，不便于实际应用［9］。另一方面，实际工程领域广泛存在着时滞现象。时滞系统的稳定化控制问题研究的重要性是不言而喻的［10-13］。

本文针对一类非线性时滞系统，设计了一种自适应神经网络动态面控制器。在每一步设计中，将未知非线性函数打包，利用径向基（RBF）神经网络逼近，并且将神经网络权重的范数定义为估计参数，这样大大降低了在线调整参数的个数。通过引入一阶滤波器，消除了传统反演设计中的计算膨胀问题。另外，本文研究的系统包括时滞项，所以该系统是具有一般性的严格反馈非线性系统。最后，理论分析证明了闭环系统所有信号是半全局一致最终有界。

2 问题的描述

考虑如下一类单输入单输出严格反馈非线性时滞系统

假设 1：未知增益函数 gi（）的符号是已知的，且存在未知正常数 gmax≥gmin＞0 使得 gmin≤/gi（）/≤gmax.不失一般性我们假设 0＜gmin≤gi（），i=1，2，…，n.

注1：假设1类似于文献［1，2，8-10，13］，应该强调的是常数gmin和gmax仅仅是为了后文的分析目的，它的实际值在控制器设计中不必已知.

为了给出假设2，我们先介绍下面的坐标变换：

这里Si是第i个误差面，vif是通过一阶滤波器得到的虚拟控制律.

假设 2：存在未知连续函数 qij（（t）+（t））使得

注2：假设2类似于文献［12］中的假设3，不过那里要求qij（·）是已知的.而本文的假设2是不需要qij（·）已知的.这放松了文献［12］对时滞项的限制.

3 自适应神经网络动态面控制设计

本节给出控制器的设计方法，控制器的设计包含n步，在每一步中将设计虚拟控制律vi，i=1，…，n-1.最后，实际的系统控制律u在第n步中给出.

步骤 i（1≤i≤n-1）：由第 i个误差面 Si=xi-vif，有

选择虚拟控制律

和自适应律

这里 ki，ηi，li，γi和 σi是正的设计常数.是 θi=gmin-1‖‖2的估计值， 这里表示理想的神经网络权重矩阵.Pi（Zi）是 RBF 基函数向量且以 Z1=［S1］∈Ωz1∩R1，Zi=［S1，…，Si，］T∈Ωzi∩Ri+1为输入向量.

注3：这里将gmin-1///2定义为被估计参数θi，可看出在每一步设计中仅有一个调整参数然而在以往的自适应神经网络设计过程中［2，3，5-7，10］，未知神经网络权重矩阵视为被估计参数，所以以往的方法中需要在线调整大量的参数，从而增加了计算负担.

为避免对虚拟控制器重复微分，导致所谓的“计算膨胀”问题，这里利用动态面控制技术消除这一问题.为此，将vi通过时间常数为i+1的一阶低通滤波器，得到滤波虚拟控制器

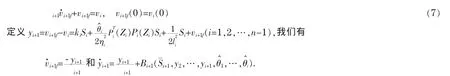
这里 Bi+1（·）是一个连续函数且具有最大值 Mi+1（详细分析可参见文献［5，6，12］）.

步骤 n：由第 n 个误差面 Sn＝xn-vnf，有

这里 kn，ηn和 ln是正的设计参数为 θn=gmin-1‖‖2的估计值，这里表示理想的神经网络权重矩阵.Pn（Zn）是 RBF 基函数向量且以 Zn=［S1，…，Sn］T∈Ωzn∩Rn+1为输入向量.

4 稳定性分析

我们考虑如下的Lyapunov-Krasovskii函数VQi和V

假设 3：对于给定的 μ＞0，存在 V（0）≤μ.现在提出如下定理：

定理1：在假设条件1-3下，考虑非线性时滞系统（1），控制器（9）和自适应律（6）所组成的闭环系统.那么对于有界初始条件（0）≥0，存在 ki，ηi，li，γi，σi和j，i=1，…，n，j=2，…，n 使得闭环系统的所有信号是一致最终有界的.

其中vn=u.通过利用（13），并注意到xi+1=Si+1+yi+1+vi，Lyapunov函数关于时间的导数为

The specific parameters of high energy nanosecond pulsed Nd:YAG laser are shown in Table 2. The laser beam travels through optical microscope, homogenized microscope and focusing lens and then irradiates onto a material surface as a circle laser beam spot.

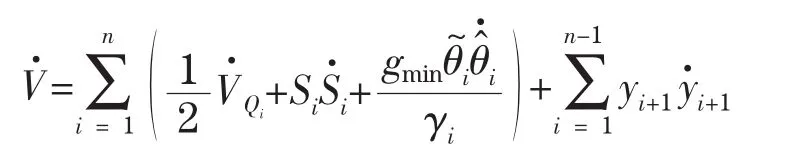
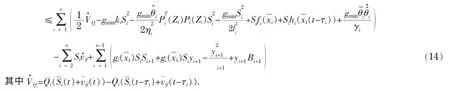
利用假设2和扬不等式，我们有

所以

将（16）代入（14）有

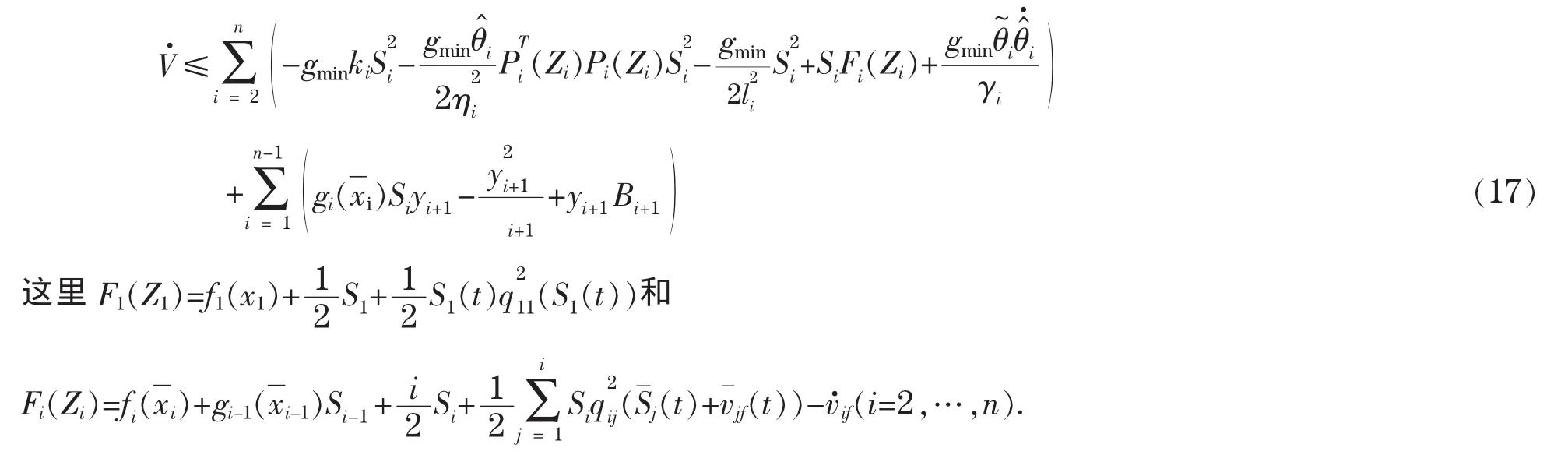
因为 Fi（Zi）是未知的函数，因此，采用 RBF 神经网络来逼近 Fi（Zi）

其中，逼近误差 δi（Zi）满足 δi（Zi） ≤εi.此外，我们有

将（18）代入（17），并且利用（6）（19）和（20）可得

注5：本文采用动态面控制方法类似于文献［12］，但本文具有以下优势：（1）本文采用神经网络逼近未知打包的非线性函数，使得控制器结构简单；（2）本文放松了对时滞项的要求；（3）对于一个n阶系统，所需在线调整参数仅需n个，大大降低了在线计算负担.

5 仿真算例

考虑如下二阶非线性时滞系统

选取τ1=1和τ2=2.则显然τmax=2.应用定理1，选择虚拟控制器、实际控制器和自适应参数如下

其中 S1＝x1，S2＝x2-v2f，Z1＝S1，Z2＝［S1，S2，］T.我们选择初始条件为［x1（t），x2（t）］T＝［0.1，-1］T，-τmax≤t≤0，v2f（0）＝0 和［（0），（0）］T＝［0，0］T.在仿真中，设计参数选取如下：k1＝3，k2＝2，l1＝l2=5，γ1＝γ2=1，η1=0.1，η2=2，σ1＝σ2＝0.2，2＝0.005.RBF 神经网络P1（Z1）包含 5 个节点，中心平均分布在［-2，2］，宽度为 1.RBF 神经网络P2（Z2）包含 125 个节点，中心平均分布在［-2，2］×［-2，2］×［-4，4］，宽度为 2.

图1-2显示了仿真结果.从图1，可看出经过几秒钟之后，状态变量x1和x2就已收敛.从图2，我们可看出自适应参数和是有界的.仿真结果说明了所提出的控制器很好的实现了控制性能.

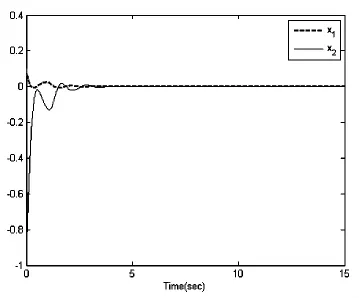
图 1.状态变量 x1（--）和 x2（-）.

图 2.自适应参数 （--）和（-）.

6 结论

本文针对一类严格反馈非线性时滞系统，提出了一个自适应神经网络动态面控制方案.应用动态面设计技术克服了传统自适应反演法中的“计算膨胀”问题.通过构造恰当的Lyapunov-Krasovskii函数，未知时滞项得到了完美处理.另外本文所设计的控制器结构简单，包含了较少的在线调整个数，使得计算负担大大减少，从而使得该方案便于实际应用.最后通过仿真实例说明了所提算法的有效性.

［1］YANG Y S，ZHOU C J. Robust adaptive fuzzy tracking control for a class of perturbed strict-feedback nonlinear systems via small-gain approach［J］.Information Sciences，2005，170（2-4）：211-234.

［2］GE S S，WANG C.Direct adaptive NN control of a class of nonlinear systems［J］.IEEE Transactions on Neural Networks，2002，13 （1）：214-21.

［3］ZHANG T P，GE S S. Adaptive neural network tracking control of MIMO nonlinear systems with unknown dead zones and control directions［J］.IEEE Transactions on Neural Networks，2009，20 （3）：483-497.

［4］SWAROOP D，HEDRICK J，YIP P，etal. Dynamic surface control for a class of nonlinear systems［J］.IEEE Transactions on Automatic Control，2000，45 （10）：1893-1899.

［5］WANG D，HUANG J.Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form［J］.IEEE Transactions on Neural Networks，2005，16 （1）：195-202.

［6］李铁山，邹早建，罗伟林.基于 DSC 后推法的非线性系统的鲁棒自适应 NN 控制［J］.自动化学报，2008，34（11）：1424-1430.

［7］ZHANG T P，GE S S. Adaptive dynamic surface control of nonlinear systems with unknown dead zone in pure feedback form［J］.Automatica，2008，44 （7）：1895-1903.

［8］CHEN W S，LI W，MIAO Q G. Backstepping control for periodically time-varying systems using high-order neural network and Fourier series expansion［J］.ISA Transactions，2010，49（3）：283-292.

［9］LI T S，WANG D，FENG G，etal.A DSC approach to robust adaptive NN tracking control for strict-feedback nonlinear systems［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2010，40（3）：915-927.

［10］GE S S，HONG F，LEE T H.Adaptive neural control of nonlinear time-delay systems with unknown virtual control coefficients［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2004，34（1）：499-516.

［11］GE S S，HONG F，LEE T H. Robust adaptive control of nonlinear systems with unknown time delays ［J］.Automatica，2005，41（7）：1181-1190.

［12］YOO S J，PARK J B，CHOI Y H. Adaptive dynamic surface control for stabilization of parametric strictfeedback nonlinear systems with unknown time delays［J］.IEEE Transactions on Automatic Control，2007，52（12）：2360-2365.

［13］WANG M，CHEN B，SHI P.Adaptive neural control for a class of perturbed strict-feedback nonlinear timedelay systems［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2008，38（3）：721-730.

Adaptive Dynamic Surface Control for a Class of Nonlinear Time-delay Systems

WANG Sheng-yu,JI Geng,ZHU Qiong-yao,LI Ling-ling,WANG Sai
(School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China)

This paper investigates the adaptive neural network dynamic surface control problem for a class of strict-feedback nonlinear systems with unknown time delays.The problem of “explosion of complexity” in traditional backstepping design is avoided by introducing the first order filter. By constructing appropriate Lyapunov-Krasovskii functions,the unknown time delay terms have been compensated.Furthermore,based on Lyapunov theory, all signals in the closed loop system are guaranteed to be semi-globally uniformly ultimately bounded.Finally,simulation results are presented to demonstrate the effectiveness of the approach.

adaptive control;neural network;dynamic surface control;nonlinear time delay system

耿继祥）

TP273

A

1672-3708（2011）03-0007-07

2011-05-16

吉 梗（1980- ），男，湖北通山人，硕士，讲师，主要从事智能控制的研究。