楔形域上Modified-Helmholtz方程的混合边值问题

黄民海

（肇庆学院 数学与信息科学学院,广东 肇庆 526061）

本文中，笔者将研究如下二维复平面楔形域Ω上Modified-Helmholtz方程的混合边值问题

其中∶Δ为二维的Laplace算子,β为常数(2β即为波数);L1＝｛(x,y)｜y＝0,0≤x＜∞｝,L2＝｛(x,y)｜y＝xtanθ,0≤x＜∞,θ＝π/2n,n＝1,2,…｝;∂Ω＝L1∪L2;g(x),f(x)均为连续函数且当x→∞时趋于零，在顶点(0,0)处满足相容性条件.

傅里叶变换方法是解决数学物理方程最重要的数学工具之一.近年来，出现了一种新型的Fokas谱变换方法[1－2]，用以求解各种类型的线性或可积性非线性偏微分方程的初（边）值问题[3－6].在某种程度上，这种方法是傅立叶变换方法的延展；但对于某些具体问题，采用Fokas谱变换方法得到的解，更便于对解的某些特性作进一步的数值分析和渐近分析.

Fokas谱变换方法主要包括以下3个步骤：1)构造方程的Lax pairs；2)通过对Lax pairs实施实时的谱分析，得到含有未知边界值的解的积分表达式；3)利用全局关系式及其某种不变性特征，求得未知的边界值，从而得到方程的解.利用这种方法，Fokas对凸多边形上的Modified-Helmholtz方程进行了研究，得到如下结论.

引理1[7]设q(x,y)在角点为z1,z1,…,zm的闭凸多边形Ω上满足Modified-Helmholtz方程（1）.若给定适当的边界条件使得方程（1）存在一个在Ω上充分光滑且连续到边界上的解，那么此解可表示为

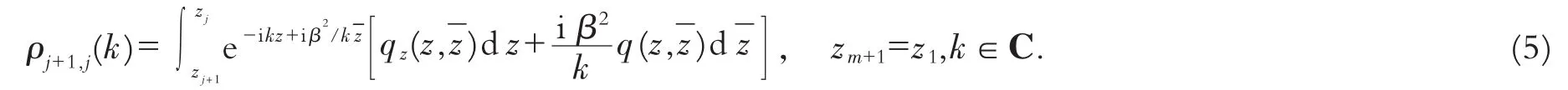
lj为从原点到无穷远点的有向射线：lj＝｛k∈C∶arg k＝－arg(zj－zj＋1),j＝1,2,…,m｝.函数ρj＋1,j(k)满足全局关系式

若Ω为开区域的情况，需要进行如下部分修改：其中，角点z1,zm分别移至无穷远点，q(x,y)(z→∞)有充分的衰减，式（4）的求和项j只有从1到m－1，函数ρ1,m(k)＝0，而ρ2,1(k),ρm,m－1(k)分别定义在S1＝｛k∈C,arg k∈[－arg(z2－z1),π－arg(z2－z1)]｝和Sm＝｛k∈C,arg k∈[－arg(zm－1－zm),π－arg(zm－1－zm)]｝上，全局关系式（6）变为

Fokas得到解的积分表达式（4）含有Dirichlet和Neumann边界值，它只能算是一种形式的表达式.对于特定的边界条件，例如Dirichlet边值问题，表达式（4）中的Dirichlet边界值为已知量，而Neumann边界值为未知量，所以，必须消除或求出其中的Neumann边界值，才能得到解的封闭积分表达式.对于特殊楔形域（张角为π/4）上Modified-Helmholtz方程的一类边值问题，已有相关研究报道[8].本文是在更一般的情况下进行讨论，文中当θ＝π/4时即为文献[8]的情况.本文所采用的方法是在文献[8]的基础上进行了推广，解决此问题的关键在于未知边界值的Riemann-Hilbert刻画.

相应于本文的问题，Ω为开区域且m＝3，楔形域的角点分别为z1＝z3＝∞,z2＝0.由引理1得到方程解的形式积分表达式

其中∶l1＝｛k∈C,arg k＝0｝,l2＝｛k∈C,arg k＝－(π＋θ)｝;

ρ21(k),ρ32(k)中含有未知的边界值，以下进一步消除这些未知量，从而得到原方程的封闭解.

在边界L1上

利用分部积分，ρ21(k)可简化为

在边界L2上，.利用分部积分可简化为

其中∶

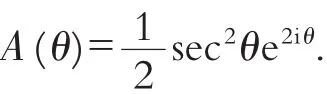
注意到未知的Q1(k),Q2(k)分别为k平面D1和D2上的解析函数.将方程（13）中的k换成－k，再取复共轭，由于将所得方程与原方程（13）相减，经整理后得

引入左半k平面解析的新函数

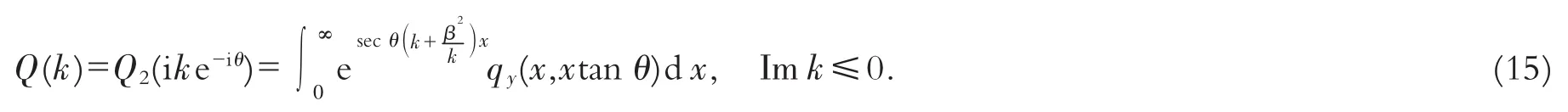
在方程（17）中取k→ke－2iθ，得

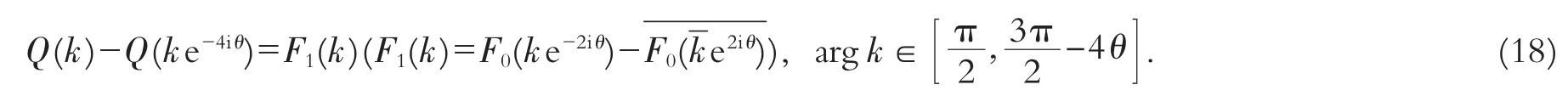
按照以上步骤继续下去，可得

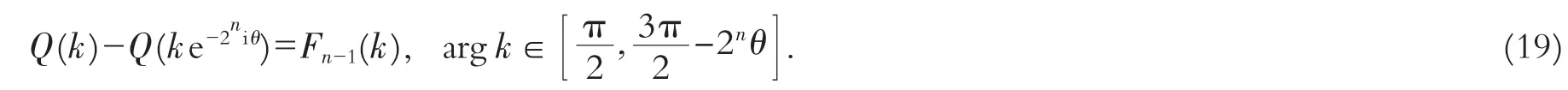
构造分区全纯函数

由方程（20）和（21），问题转化为如下关于Φ(k)在虚轴上的Riemann-Hilbert边值问题

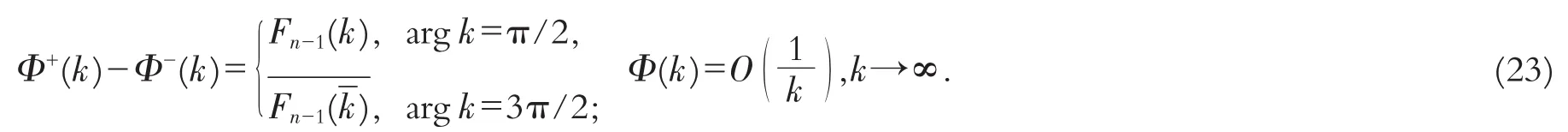
解之得

将所得结果（24）逐步回代到（22），（15），（13），（12），（11），得到 ρ21(k),ρ32(k)的值分别为

进一步将ρ21(k),ρ32(k)代回式（8），即可得到混合边值问题（1）～（3）解的封闭积分表达式.

∶

[1] FOKAS A S.A unified transform method for solving linear and certain nonlinear PDEs[J].Proc Roy Soc London Ser A,1997,453: 1 411-1 443.

[2] FOKAS A S,PELLONI B.Method for solving moving boundary value problems for linear evolution equations[J].Phys Rev Lett, 2000,84(21):4 785-4 789.

[3] ANTIPOV Y A,FOKAS A S.The modified Helmholtz equation in a semi-strip[J].Math Proc Cambridge Philos Soc,2005,138(2): 339-365.

[4] FOKAS A S,ITS A R,SUNG L Y.The nonlinear Schrödinger equation on the half-line[J].Nonlinearity,2005,18(4):1 771-1 822.

[5] TREHARNE P A,FOKAS A S.Initial-boundary value problems for linear PDEs with variable coefficients[J].Math Proc Cambridge Philos Soc,2007,143(1):221-242.

[6] DASSIOSG,FOKASAS.MethodsforsolvingellipticPDEsinsphericalcoordinates[J].SIAMJApplMath,2008,68(4):1080-1096.

[7] FOKAS A S.Two-dimensional linear partial differential equations in a convex polygon[J].Proc Roy Soc London Ser A,2001,457: 371-393.

[8] BEN-AVRAHAM D,FOKAS A S.The solution of the modified Helmholtz equation in a wedge and an application to diffusionlimited coalescence[J].Phys Lett A,999,263(4):355-359.