春季华南沿海海-气边界层动力参数的观测研究*
2011-01-10马应生
黄 菲,马应生,黄 健
(1.中国海洋大学海洋-大气相互作用与气候实验室,山东青岛266100;2.广州热带海洋气象研究所海洋气象联合开放实验室,广东广州510080;3.南海舰队海洋水文气象中心,广东湛江524001)
对海洋与大气之间的通量交换的研究,目前已成为气象和海洋研究中的重要前沿课题之一。海-气之间包括热量、水汽交换和动量传输等过程都离不开边界层,正因为如此,对海-气边界层的研究已成为海-气相互作用研究的关键环节。近年来国内外已开展了许多海-气界面观测试验,如“热带海洋与全球大气-海洋大气耦合响应试验”(TOGA-COARE)、“中尺度海-气相互作用试验”(MASEX)、“全球大气研究计划大西洋热带试验”(GA TE)等等。国内这方面的观测试验最早在南海进行,比如“南沙群岛及其邻近海区综合考察”项目、“南海季风试验”(SCSM EX)等,均以通量观测为主。南海作为中国近海中唯一的热带海区,对中国气候有着非常重要的影响。1994年9月南沙科学考察曾在渚碧礁上进行过短期湍流测量;1997年冬季在南海南部海区进行了短期感热和潜热通量的梯度测量;1998年“南海季风试验”(SCSM EX),在西沙进行较大规模的海-气通量观测计划,至今已开展4次(1998、2000、2002、2008年)试验,并获取了前3 a 5~6月和2008年5月~2009年4月近海面风速、温度、湿度等气象要素的梯度和脉动以及辐射资料。相应于这些大量的观测试验,人们对南海热通量作了很多研究[1-6],对整个南海热通量和辐射已经有了比较全面的认识,但是对南海海-气边界层的大气湍流结构特征的研究相对较少。众所周知,研究和掌握海-气边界层中的湍流结构的特征和规律,无论是对参数化方案还是对其它气候研究与应用等各方面都无疑是非常重要的。马耀明等[7-8]利用1994年9月18~30日南沙群岛渚碧礁海域的近海面大气湍流实测资料,首次研究了南沙群岛渚碧礁附近海域的大气湍流结构和输送特征,计算得到了该海域的拖曳系数CD=(1.54±0.24)×10-3。高志球等[9]利用相同的资料,分别计算了该海域光滑海面和粗糙海面上的空气动力粗糙度、中性曳力系数,并利用Brutssert的假定推导了1组求取标量粗糙度和整体输送系数的公式。闫俊岳等[10]利用1998年在西沙永兴岛近海铁塔上观测的海-气通量数据,分别用涡动相关法和廓线法计算了曳力系数、动量、感热、潜热通量及湍流强度等一些统计量的分布;闫俊岳等[11]利用2002年第3次南海海-气通量观测试验资料,用涡动相关法和TOGA-COARE2.5b版本通量计算方案,计算了西南季风爆发前后海-气界面动量、感热通量、潜热通量的湍流交换系数,讨论了各通量交换系数的变化特征及其与气象要素变化的关系。从这些研究工作中可以发现,在南海,不同的观测试验海区、不同的研究方法,对大气湍流结构及它的一些特征的研究结论并不一致。同时,这些观测试验基本都在离海岸较远的深海区,主要集中在西沙和南沙,而南海北部的海岸带(华南沿海)地区,这个海陆交错的关键区域却缺少类似的研究。因此,本文采用2006年3~5月在珠江口地区连续的实测资料来分析该区域边界层湍流结构的一些特征,以期初步了解这一地区的海-气边界层特点。
1 观测资料与处理方法
数据来自中国气象局广州热带海洋气象研究所2006年3月5日~5月29日在珠江口的海雾观测试验。观测点设在珠海市九洲港码头南端的海岸上(22°14′03″N,113°35′05″E)。观测点三面环海,只有偏北方向(315(°)~360(°)和0(°)~45(°))是陆地(见图1),因此由涡动相关系统观测的风速等气象要素受地形影响较小。本文主要用到的风速数据,由CAM PBELL涡动相关系统中的CSA T3超声风温仪测量,其安装高度距离海平面3.9 m,采样频率为10Hz,观测数据由CR5000数据采集器采集。由于超声的安装足够靠近岸边,能较好地捕捉到来自海面风的信号。观测从3月5号早晨开始,5月29日下午结束,观测期间由于供电等因素的影响导致若干次的观测中断和数据不连续,其中缺测最长的时段是5月6日12··00~5月8日14··00(超过2 d时间),其余时段的观测中断时间都较少。

图1 观测位置Fig.1 Observational location
本文根据Vander Hoven风速谱[12]和Kaimal等[13]对平均时间的算法,统计时间序列长度取为30 min,用每小时的前30 min采样作为统计样本,首先进行预处理,具体步骤为:
(2)坐标旋转,将笛卡尔坐标系下的风速进行2次坐标旋转到自然风坐标系下[14-16];
(3)数据趋势剔除,得到脉动值。
上述观测仪器和数据预处理方法与黄健等[17]在研究分析华南沿海暖海雾过程中热通量的处理方法基本一致,并对后期计算结果进行了降水剔除。空气过于潮湿会影响超声仪器的精确度,为了精确起见,剔除降水和降水后1个时次,最后挑选出来的有效样本数接近1 700个。
2 结果分析
2.1 大气稳定度与摩擦速度
采用涡动相关法计算大气稳定度和摩擦速度:


图2 大气稳定度概率分布Fig.2 The p robability density distribution of atmospheric stability
从图2可以看出,稳定度的概率分布基本可以看作正态分布或者近似正态分布,峰值略微偏向负值。样本中的绝大数稳定度都在±0.2之间,占总数的88%,说明此季节内观测区域边界层的大气状态基本为中性或近中性的状态,强不稳定和强稳定天气过程相对很少。在整个观测期间,也观测到了几次观测区域春季经常出现的海雾和冷空气活动过程,因此本文的统计结果具有一定的代表性。
摩擦速度是1个边界层中很重要的参数,是计算很多参数的基础,掌握其变化规律显得尤为重要。采用超声数据和涡动相关法的优点是可以用风速的脉动直接计算,即从定义出发计算而得,不经过迭代等方法,使其有较高的精确度。本文计算的摩擦速度平均值为0.207,与闫俊岳等[10]在1998南海季风爆发前后在西沙的计算结果相同,说明此参数在南海北部直至近海海岸带都有一定的适用性。鉴于此次观测时间足够长、基本涵盖了整个春季,此结果应该更加准确和可信,弥补了上述研究工作由于观测时间较短(只在季风爆发前后短时间内进行观测)而使人对其结果产生的疑虑。摩擦速度不仅是风速的函数(见图3),还与大气层结有关(见图4)。从摩擦速度与风速的关系来看,总体上其与风速成线性关系,二者可拟合为关系式

拟合数据1 682组,显著性检验超过99%信度,二者相关系数超过0.99。无论是在稳定、不稳定或者中性层结下,摩擦速度都是随风速而增大。从图3中可以看出,对二者的线性关系离散性影响最大的是地形因素,偏北风向(315(°)~360(°)和0(°)~45(°))下的数据的离散性明显高于其它方向从海面吹来的风。为了分析摩擦速度在不同稳定度下与风速的关系,本文只选取受地形影响最小的偏南风时的数据(见图5),在相同风速的条件下,相比拟合曲线,摩擦速度在ζ=z/L>0.2的层结(较稳定)中小于其在ζ=z/L<-0.2层结(较不稳定)中,最大的是在|ζ|<0.2的这个近中性的层结中,且ζ<0的点的离散性大于ζ>0的点,但是比地形对摩擦速度的离散性的影响要小很多。

图3 摩擦速度与不同风向下平均风速的关系Fig.3 Frictional velocity varying with average w ind speeds in different direction
摩擦速度和稳定度的关系(见图4),类似大气稳定度的概率分布,绝大多数的点都落在稳定度的±0.2内,峰值也偏向负值。不同风速条件下摩擦速度与稳定度的分布也不尽相同,本文将12 m/s内的实测风速分为3部分。在不同的风速阶段内,摩擦速度随稳定度的分布变化比较明显。当U≤4 m/s时,摩擦速度分布最广,平均值最小为0.158,对应的稳定度的变化范围也最大;U在4~8 m/s之间时,稳定度变化范围明显变小,且ζ=z/L>0的变化范围大于ζ=z/L<0的变化范围,这个风速段内的摩擦速度的平均值为0.245;U在8~12 m/s之间时,稳定度变化范围都在±0.2内,此时段内的摩擦速度的平均值最大为0.410。

图4 摩擦速度随稳定度的变化关系Fig.4 Variation of frictional velocity with respective to atmospheric stabilities

图5 偏南风时摩擦速度在不同稳定度下与平均风速的关系Fig.5 Frictional velocity varying with average wind speedswith its direction between 135(°)and 225(°)in different stabilities
2.2 无因次风速方差相似规律
根据Monin-Obukhov相似理论,任何1个量的标准差被特征尺度参数无量纲化后应为稳定度ζ=z/L的普适函数,即在近地面层风速的标准差经过无量纲化后为稳定度的函数:

式中z为测量高度,<α(α=u,v,w)分别为u,v,w方向上的风速方差普适函数,σα为3个方向风速分量的标准差。当Lµz时,ζ=z/L趋近于0,即大气处于中性或近中性层结,此时近地层湍流主要由机械生成,各相似函数分别为常数,即有:σu/u*=A、σv/u*=B、σw/u*=C。本文通过分析发现,观测区域内的边界层中的风速方差很好地满足1/3次方相似规律(见图6)。当ζ=z/L趋近于0时A,B,C的值分别为3.06、2.56、1.33。对于此常数参数,在不同的下垫面进行观测试验时得出的结论也不同,以海洋和陆地为下垫面的结果差别也较大。陆地上参考较多的是Panofsky等[18]研究了10种不同下垫面后得到的参数常数,A,B,C分别为2.39、1.92、1.25。国内也有较多有关的实验,比如wang[19]在典型的山谷城市兰州市观测试验A=3.36,B=2.4,C=1.31;卞林根等[20]在青藏高原南部也做过类似观测试验。在南海这方面的工作主要有2个,分别在南沙[7]和西沙[10],二者所给出的3个常数参数分别为A=2.32、B=1.76、C=1.2和A=3、B=2、C=1.25。海岸带的下垫面比单一的陆地或者海洋下垫面更复杂一些,海面来向的风和陆地来向的风的差异应该较大,但是也应该比起伏较大的陆地受地形因素的影响较小。相比之下,本文的结论更接近西沙海域。无因次风速方差很好地满足相似理论这一事实可以表明:风速方差的相似函数也可以在南海北部近海(华南沿海)使用,中性条件下普适函数为常数,本文拟合了在稳定与不稳定2种层结下的无因次风速方差的普适函数:


图6 无因次风速方差随大气稳定度的变化关系Fig.6 Non-dimensional wind standard deviation in different atmospheric stabilities
从图6同时还可以看出1个问题:正如前人的研究工作[21-22]所指出的那样,水平方向风速方差的离散性大于垂直方向。由于稳定度ζ=z/L是与热力作用有关的参数,相比水平方向,垂向湍流的发展和热力作用的关系更大,图6中垂向无量纲化的风速方差的离散性比水平方向小,说明垂向的湍流主要取决于热力因子,受其他因子影响很小,而影响水平方向湍流的因素可能比较多,也比较复杂,赵鸣[23]等指出影响水平湍流的1个主要因子可能是水平风场对湍流的作用。对比ζ=z/L>0与ζ=z/L<0这2种情况可以看到:ζ=z/L<0时,无量纲化的风速方差离散度略大,在垂向图上表现得更明显。
2.3 湍流强度
湍流强度简称湍强,是衡量湍流强弱的指标。计算公式为:Iα=σα/U,其中Iα(α=u,v,w)为水平与垂直方向的湍流强度分量,U为观测高度的自然坐标下的30 m in平均风速。为尽量减少观测数据受地形影响产生扰动,本文在统计湍流强度特征的时候,不考虑偏北风(风向角在315(°)~360(°)和0(°)~45(°))条件下的样本。统计结果显示,平均湍流强度分别为:Iu=0.208,Iv=0.189,Iw=0.099。前人的研究工作中,距离珠江口比较近的观测试验点是南海西沙[10],三者的观测平均值为0.096、0.066、0.04,本文的结果偏大有2个原因,主要原因是西沙的观测分析中没有考虑风速小于2 m/s的情况,从图7可看出,风速小于2 m/s时,湍流发展最为旺盛,这就是通常说的自由对流状态,此时湍强平均值为Iu=0.389,Iv=0.383,Iw=0.183,接近平均值的2倍,样本数占有效样本的24.9%,可见自由对流状态下的湍强对平均湍流强度贡献的大小;另一个原因可能是,相比以单一的海洋为下垫面,海岸带的地形更复杂、海-气温差等相关要素差异更大,促使近地面层中大气与下垫面的相互作用更加活跃,湍流的发展更旺盛。湍强与风速的关系,在风速小于4 m/s的时候,湍强均随风速减小而增大,尤其是在自由对流状态下,随风速的减小而迅速增大;风速在4~6 m/s时,湍强的变化不明显;当风速大于6 m/s时,湍强随风速的增大略有增加,并且水平分量比垂直分量的变化要明显,说明较高的风速更有利于水平方向湍流的发展,同时也说明垂向湍流的发展对动力因子的依赖程度较小。
从图7还可以看出湍流强度与大气层结的关系,在相同的风速条件下,湍流强度较大的点,在ζ<0的层结中明显多于在ζ>0的,即不稳定层结比稳定层结更有利于湍流的发展,从表1也可看出,湍流在不同稳定度下的平均强度的差异,稳定层结中湍强最弱,不稳定条件下湍流交换能力最强,说明稳定层结中最不利于湍流的发展,中性或者近中性和强不稳定层结中,都有利于湍流的发展,在这2种层结中,垂向分量湍强的增幅是最大的,再次说明垂向湍流的发展与大气及其下垫面的热力关系更紧密。各湍强分量在近中性条件下的值基本接近季节平均值,这主要归因于近中性层结的样本占绝大多数、强稳定和强不稳定过程相对较少。总体上,不同稳定度下Iu略大于Iv,但是基本存在Iu≈Iv>Iw的关系。

图7 湍流强度随风速的变化关系Fig.7 Turbulent intensity varying with wind speeds in different stabilities

表1 不同稳定度下平均湍流强度Table 1 Hourly-mean turbulent intensity in different stabilities
上述分析表明,垂向湍流强度比水平向湍流强度更依赖于热力因子,在大气与下垫面相互作用的过程中,热源主要来自下垫面,而下垫面的热力状况应该有较明显的日变化,为证实垂向湍流的发展与热力因素的关系,本文分析了垂向湍流强度与海-气温差、湍强频次的日变化关系(图略)。结果发现,无论是自由对流状态还是全部样本,海-气温差在08··00左右达到最大,这时段内的湍强的离散型最大,同时湍强出现的频次也最大;其次,海-气温差在傍晚(17··00前后)的震荡较大,此时也有较强的湍流发展,湍强发生的频次也较高,离散型也较强。这表明,大气与下垫面之间的温差增大会导致湍强尺度上和频数上都有大幅地增大,垂向湍流的发展重要取决于热力因子。
2.4 海面空气动力粗糙度
海面空气动力粗糙度Z0定义为风速在海平面之上某处为0 m/s时的高度,它和海面状况有关。本文只考虑从海面吹来的风,采取和统计湍强时一样的方法来去掉偏北风的影响,并用Sm ith[24]推荐的Charnock关系式[25](这也是COARE2.5[26]版本提供的算法之一)加以计算:
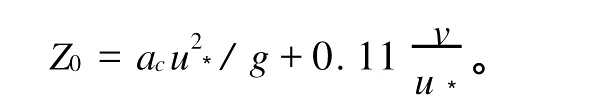
Z0由粗糙海面和光滑海面的粗糙长度2项组成。其中ac为Charnock常数,其值在0.015~0.035之间,海洋上ac=0.016。V为运动学粘性系数,是气温的函数:

由于本文所用数据不是正好在海面10m高处采集所得,所以用以下公式计算出海面10m处风速。在中性或近中性层结条件下,对数风廓线k U/u*=ln(z/Z0)始终成立[9],k为卡曼常数,取为0.4。根据风廓线计算的海面10 m高处风速U10,Z0随U10的变化关系如图8所示,二者的变化关系可以拟合为二次曲线:

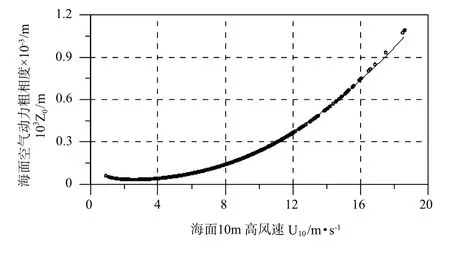
图8 海面空气动力粗糙度与10 m高风速关系Fig.8 Sea surface aerodynamic roughness varying with 10 m average w ind speed
拟合数据1 367组,相关系数超过0.99。当U10=3.0 m/s时Z0达到极小值,约为0.036×10-3m。此结果表明可将观测海区10 m高风速U10=3.0 m/s视为光滑海面、粗糙海面的分界点。此计算方法和结果均与高志球等[9]根据雷诺数与运动学粘性系数的关系,将海面9.4 m高的风速U9.4=4 m/s作为南沙渚碧礁附近海区的光滑与粗糙海面的分界点略有不同。空气动力粗糙度随风速的变化在拐点前后不大,这是因为在风速逐渐增大时,海面的状况从光滑状态到粗糙状态有1个过渡,粘性副层和粗糙海面同时存在。当U10在2.0~4.0 m/s之间时,即在拐点附近,Z0的值很小,变化幅度也很小;风速继续减小时(U10<2.0 m/s),粗糙度随着风速的减小略有增加,说明此观测海区的光滑海面也存在粘性副层;当U10>4.0 m/s时,Z0随着风速的增大明显曾大。
2.5 中性拖曳系数
拖曳系数是海-气通量交换的1个重要参数,是计算整体输运系数的基础。根据涡动相关法动量通量的计算公式:

和对数风速廓线可直接算得大气在中性层结下的拖曳系数。本文计算的平均值为Cd=1.180×10-3,此结果文献[11]在西沙的观测试验结果(Cd=1.029×10-3)接近,略微偏大的原因是本文的观测数据包括了较多的高风速时次(见图9)。根据比较计算,Cd和风速U10的关系以U10=4 m/s作为分段点来拟合时,二者关系达到最好:

U10≈4 m/s时Cd约为1.040×10-3。U10<4 m/s拟合数据297组,相关系数大于0.98;4 m/s

图9 中性拖曳系数与10 m高风速关系Fig.9 Drag coefficient varying with 10 m average wind speed under neutral conditions
3 结论
本文利用中国气象局广州热带海洋气象研究所2006年3月5日~5月29日在珠江口进行海雾观测所得的超声资料,初步分析了2006年春季南海北部海岸带地区边界层的湍流结构的一些特征,得到一些基本结论如下:
(1)大气稳定度的概率密度分布基本呈正态,此季节内观测区域近地面层的大气层结基本为中性或近中性的状态,强稳定或者强不稳定的天气过程很少。摩擦速度不仅和风速有关而且和大气层结稳定度有关,其随风速线性增加,与风速的线性关系中,地形对其离散性影响较大。
(2)无因次风速方差符合1/3次方的相似规律,在稳定度ζ=z/L趋近于0时,u,v,w分量所对应的相似函数为常数,分别为3.06、2.56、1.33;本文进一步给出了风速在各个分量方向的普适函数。
(3)平均湍流强度分别为Iu=0.208,Iv=0.189,Iw=0.099。风速在小于4 m/s的时候,湍强均随风速减小而增大;风速在4~6 m/s时,湍强变化不明显;风速大于6 m/s时,湍强随风速的增大而略有增加,且水平方向的增加量大于垂向。湍流的发展在中性或者近中性条件下非常接近平均状态,但在不稳定层结中是最强的,垂向湍强从中性层结到不稳定层结的增幅基本是水平向湍强的增幅的两倍。
(4)海面动力空气粗糙度Z0在U10=3.0 m/s附近达到最小,在观测区域内可将U10=3.0 m/s作为光滑海面和粗糙海面的分界点。其与风速的关系可拟合成二次曲线,当U10在2.0~4.0 m/s之间时,Z0的值很小,变化幅度也较小,风速继续减小时,粗糙度随着风速的减小略有增加,当U10>4.0 m/s时,Z0随着风速的增大明显曾大。
(5)中性条件下拖曳系数Cd的平均值Cd=1.180×10-3。在U10=2.7 m/s时,Cd达到最小。Cd和风速U10的关系以U10=4 m/s为分界点时的拟合关系最好,在U10<4 m/s时,Cd随风速先减小后增加,为二次曲线关系;当U10在4~20 m/s之间时,Cd随其线性增加。
[1] 孙即霖,刘秦玉,张秀芝.1998年夏季风爆发前后南海海气热通量主要特征.南海季风爆发和演变及其与海洋的相互作用[M].北京:气象出版社,1999:152-156.
[2] 许建林,曲绍厚.1997年冬季南海南部海区不同天气过程下的湍流通量输送[J].热带海洋,2000,19(2):19-26.
[3] 闫俊岳,姚华栋,李江龙,等.2000年南海季风爆发前后西沙海域海-气热量交换特征[J].海洋学报,2003,25(4):18-28.
[4] Jiang Gourong,He Jinhai,Wang Dongxiao,et al.Observational study of air sea fluxes during the SCS summer monsoon in 20002 Featuresof thermal budget at the sea surface[J].Acta Meteorologica Sinica,2004,18:245-258.
[5] 闫俊岳,唐志毅,姚华栋,等.2002年南海西南季风爆发前后海-气界面的通量交换变化[J].地球物理学报,2005,48(5):1000-1010.
[6] 陈奕德,蒋国荣,张韧,等.2002年南海夏季风爆发期间南海北部海气通量分析与比较[J].大气科学,2005,29(5):761-770.
[7] 马耀明,王介民,刘巍,等.南海海域近海面层大气湍流结构及输送特征研究[J].大气科学,1997,21:357-365.
[8] 马耀明,王介民,张庆荣,等.南沙海域大气湍流通量输送特征分析[J].高原气象,1997,16(1):45-51.
[9] 高志球,马耀明,王介民,等.南沙群岛海域近海面粗糙度、中性曳力系数及总体交换系数研究[J].热带海洋,2000,19(1):38-42.
[10] 闫俊岳,姚华栋,李江龙,等.1998年南海季风爆发期间近海面层大气湍流结构和通量输送的观测研究[J].气候与环境,2000,5(4):447-458.
[11] 闫俊岳,唐志毅,姚华栋,等.南海西南季风爆发前后海-气通量交换系数研究[J].气象学报,2006,64(3):335-344.
[12] Vander Hoven I.Power spectrum of horizontal wind speed in the frequency range from 0.0007 to 900 cycles per hour[J].Journal of the Atmospheric Sciences,1957,14:160-164.
[13] Kaimal J C,Finnigan J.Atmospheric boundary layer flow s:Their structure and measurement[M].Oxford:Oxford University Press,1994:266
[14] Finnigan J J,Clement R,Malhi Y.Are-evaluation of long-term flux measurement techniques.Part I:averaging and coo rdinate rotation[J].Bound-Layer Meteor,2003,107:1-48.
[15] Finnigan J J.A re-evaluation of long-term flux measurement techniques.Part II:Coordinate systems[J].Boundary-Layer Meteorology,2004,113:1-41.
[16] Wilczak J,Oncley S,Stage SA.Sonic anemometer tilt correction algorithms[J].Boundary-Layer Meteorology,2001,99:127-150.
[17] 黄健,王斌,周发琇,等.华南沿海暖海雾过程中的湍流热量交换特征[J].大气科学,2010,34(4):715-725.
[18] Panofsky H A,Dutton J A.A tmospheric turbulencemodels and methods for engineering applications[M].New York:Wiley-Iinterscience,1984.
[19] Wang J.Turbulence characteristics in an urban atmosphere of comp lex tertian[J].Atmospheric Environment,1992,26A(15):2714-2717.
[20] 卞林根,陆龙骅,程彦杰,等.青藏高原东南部昌都地区近地层湍流输送的观测研究[J].应用气象学报,2001,12:1-13.
[21] Andreas E,Hill R J,Gosz J R,et al.,Statistics of surfacelayer turbulence over terrain with metre-scale heterogeneity[J].Boundary-Layer Meteorology,1998,86:379-408.
[22] Choi T,Hong J,Kim Joon,et al.,Turbulent exchange of heat,water vapor,and momentum over a Tibetan prairie by eddy covariance and flux variance measurements[J].J Geophys Res,2004,109,D21106,doi:10.1029/2004JD004767.
[23] 赵鸣,苗曼倩,王彦昌.边界层气象学[M].北京:气象出版社,1991:465.
[24] Smith SD.Coefficients for sea surface w ind stress,heat flux and wind p rofiles as a function of wind speed and temperature[J].J Geophys Res,1988,93(C12):15467-15472.
[25] Charnock H.Wind stress on a water surface[J].Quart J Roy Meteor Soc,1955,81:639-640.
[26] Fairall CW,Bradley E F,Rogers D P,et al.Bulk parameterization of air-sea fluxes for Tropical Ocean-Global Atmosphere Coupled-Ocean Atmosphere Response Experiment[J].J Geophys Res,1996,101(C2):3747-3764.
[27] Yelland M,Moat B I,Taylor P K,et al.Wind stress measurements from the open ocean corrected for airflow distortion by the ship[J].J Phys Oceanogr,1998(28):1511-1526.
