Mn掺杂MgF2光学性质的第一性原理研究

贾 牧，龙绍唐

（ 1.山东大学 机械工程学院，山东 济南 250100；

2.铜仁学院 物理与电子科学系，贵州 铜仁 554300 ）

Mn掺杂MgF2光学性质的第一性原理研究

贾 牧1，龙绍唐2

（ 1.山东大学 机械工程学院，山东 济南 250100；

2.铜仁学院 物理与电子科学系，贵州 铜仁 554300 ）

采用基于密度泛函理论（DFT）第一性原理平面波超软赝势方法计算Mn掺杂MgF2晶体的几何机构、电子结构和光学性质。结果表明，经过Mn掺杂MgF2的浓度为12.5%时，体系的结构并没有发生明显的结构畸变或相变。但体系的能带结构，尤其是费米面附近的能带结构有重要的影响。对吸收光谱和介电常数有所调制，结果与实验测量大致吻合。

MgF2； 掺杂； 电子结构； 光学性质； 第一性原理

1.引言

MgF是一种红宝石结构，用于制造陶瓷、玻璃、冶金镁金属的助熔剂，阴极射线屏的荧光材料，焊剂；也是一种重要的固体发光器激光介质，可制造透镜、窗口、光学棱镜等光学元件。有些氟化镁单晶用在军工和光通信系统领域[1]。它还作为非常规则的催化剂载体，可以使有机化合物液态脱硫、催化氧化一氧化碳以及消除氧化氮等方面的催化剂获得很好的催化活性，在环保方面有很大的用处。[2][3][4]过渡金属原子掺杂MgF2晶体，使其性能发生了很好的变化，为了调制和运用它更优异的性能，过渡金属原子掺杂MgF2晶体成为近期一个研究热点。Mn作为具有代表性的过渡金属，也自然成为讨论的重点。例如，Rao等[5]对MgF2：Mn的光谱做出了解释；Remme等[6]测得了MgF2：Mn2+的光谱和电子顺磁共振（EPR）谱；Zhao[7]发展了一种新方法，采用EPR超精细结构常数A，确定杂质中心局部结构，计算所得的局部杂质结构健长精确到了0.001nm；谢林华等[8]基于EPR超精细结构常数A，确定健长的新方法和Zhao的半自洽场轨道理论，对MgF2：Mn2+光谱和EPR超精细常数作出了统一解释。然而，MgF2：Mn的结构和光学

2性质在理论研究方面研究甚少，因此可以从理论研究方面对其深入探究。

本文应用第一性原理平面波超软赝势方法计算Mn掺杂MgF2晶体的几何机构、电子结构和光学性质。研究了Mn掺杂MgF2晶体的静态介电常数、禁带宽度和光学吸收系数，所得的结果与实验测量有很好的吻合。这对MgF2和MgF2：Mn的制备以及其它相关材料在光学器件方面的运用有所参考。

2.结构模型和理论方法

理想MgF2是四方红宝石结构，属于P42/mn空间群，晶格常数为：a=b=0.4615nm，c=0.3043nm[9]，α=β=γ=90°。本文计算中采用的MgF2（2×2× 1）超原胞模型，如图1（a）所示。超原胞模型由4个MgF2单胞组成，每个MgF2单胞包含2个Mg原子和4个F原子，总共24个原子。当其中一个Mg原子被一个Mn原子替代后，掺杂浓度是12.5%，就形成了Mn0.125Mg0.875F2三元合金（如图1（b）所示）。

2.1. 结构模型

2.2. 理论方法

本文基于第一性原理计算的密度泛函理论（Density Functional Theory）结合平面波赝势方法的CASTEP[10][11]（Cambridge Serial total Energy Package）软件包。在计算中，应用周期性边界条件，用广义梯度近似（GGA）的PBE来处理电子间的交换关联能，而对于电子波函数则通过平面波基矢组扩展，且用超软赝势[12]（ultrasoft pscudopoterntial）描述离子实与价电子之间的相互作用势，选取Mn，Mg，F各原子的价电子组态分别为Mn−3d54s2，

Mg−2p63s2，F−2s22p5[13]，Mn原子的初始自旋极化设置为 3。在倒易K空间中，平面波截断能Ecut=450eV，迭代过程中的收敛精度为2× 10−5/原子，作用在每个原子上的力不大于0.1eV/10−10，内应力不大于0.1GPa。全布里渊区域的求和使用4×4×2的K点网络。计算在倒易空间中进行，获得晶胞的最优化结构，并在这个基础上进一步计算电子结构等性质。

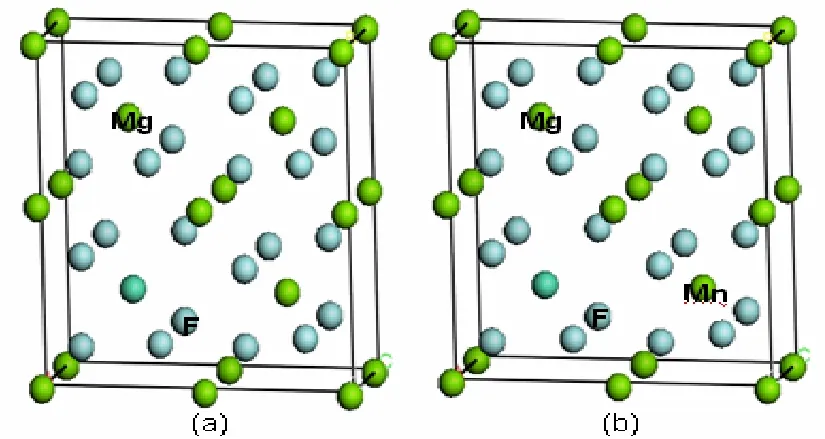
图1 Mn0.125Mg0.875F2超原胞透视图

3.结果和讨论

3.1. 理想 MgF2

MgF超原胞进行优化，优化后的体系晶格结构参数如表1所示。

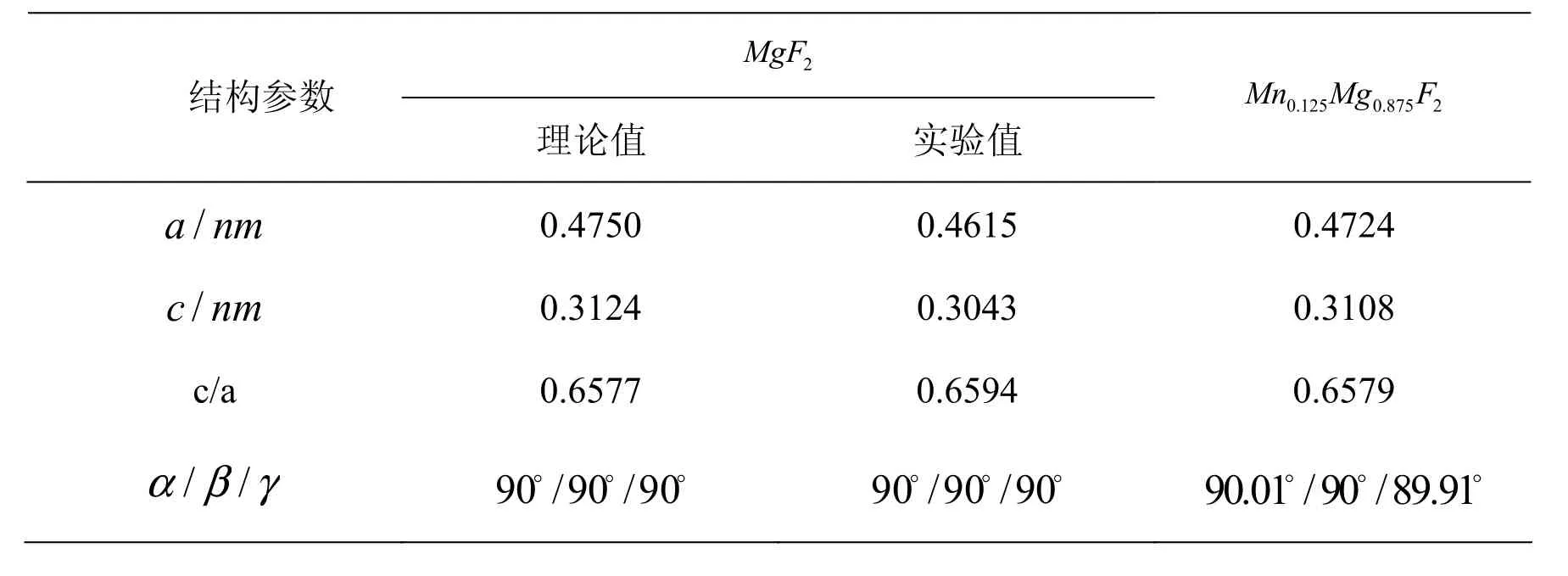
表1 Mn掺杂前后晶胞晶格常数

由表 1可以看出，优化后得到c/a的理论值为0.6577与实验值0.6594偏差约为0.26%，说明理论计算结果可靠。基于优化的几何结构，计算MgF2晶体的能带结构，结果如图2所示。

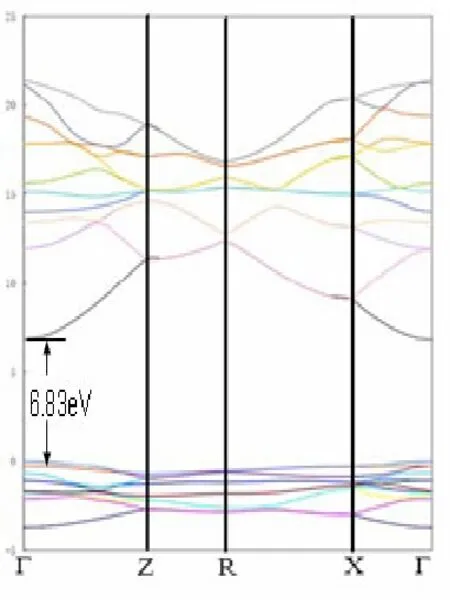
图2 MgF2的能带结构

由图2可知，MgF2的禁带宽度最窄的地方是Γ点，是直接带隙材料。在Γ点导带与价带之间带隙的宽度为6.83eV与文献结果6.97eV[14]大致吻合，该值与实验值10.08eV[15]相比较有些偏小。这主要是由于局域密度近似（LDA）存在的误差的普遍结果，使得Eg计算值偏低[16][17]。由于本文主要讨论Mn掺杂后材料结构性质的变化以及对其光学性能的影响，因此误差对本文讨论可以忽略。

3.2. Mn：2 MgF

3.2.1.Mn：MgF2的几何结构

通过计算得出的Mn掺杂下Mn0.125Mg0.875F2的晶体最优化结构。为了方便比较，Mn掺杂前后的晶格常数见表1。由表1可以知道，通过Mn的掺入，MgF2的晶格常数的影响较小。由于Mn的离子半径0.046nm

小于Mg离子半径0.065nm，Mn以代位的形式掺杂时，晶胞的体积会有所减小，但键角变化不大。表明通过Mn的掺杂晶格并没有发生明显的结构畸变。

3.2.2.Mn：MgF2的电子结构

Mn掺杂后，Mn0.125Mg0.875F2电子结构也发生较小的变化。当一个Mn原子取代一个Mg，其能带图如图3所示。

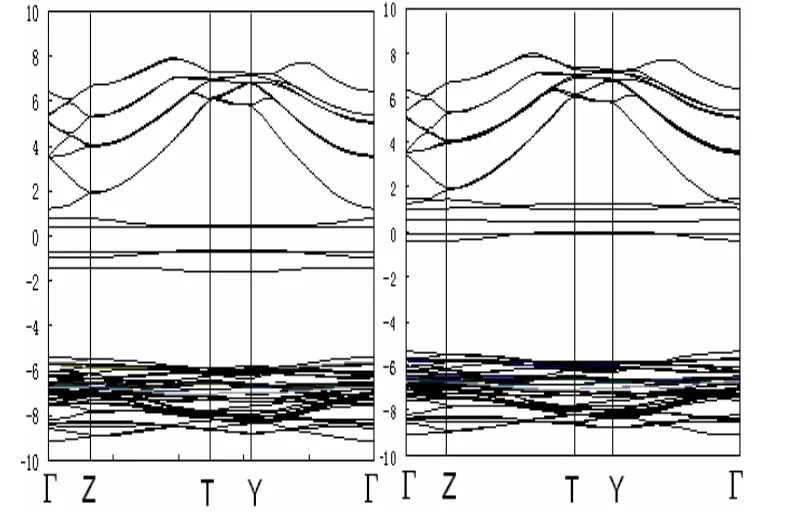
图3 Mn0.125Mg0.875F2的能带图

由图 3中可以看出，自旋向上态的Mn0.125Mg0.875F2能带在费米面附近产生了杂质能带；自旋向下的费米面附近也产生杂质能带，且更复杂。这是由于Mn原子的掺杂引入了d电子态，使d电子能级在费米面附近展开成为能带，使得费米面处在这能带中，导致自旋向上和自旋向下都没有能隙。与图2比较可知，体系的能带结构发生了改变。

在图4中计算了Mn0.125Mg0.875F2的总态密度和不同原子分态密度，其中（a）、（b）、（c）分别是Mn、Mg、F的分态密度图；（d）是总态密度图。将图中的态密度进行比较，可以看出：从−9eV到−5eV附近的峰值要是由F-2p轨道贡献，而Mg的3s轨道和Mn-3d轨道贡献甚少；从−2eV到2eV主要来自于Mn-3d轨道贡献，F的自旋向上的2p轨道贡献很少；费米面上的带主要由Mn自旋向下的3d轨道贡献；从2eV以的的导带主要来自于Mn-4s轨道以及Mg-2p和-3s轨道贡献；除此以外，由图4（c）可以看出，Mn的掺入后对F产生了重要的影响，费米面附近出现了一些附加的小峰。这些说明，Mn的掺入对体系的能带结构，尤其是费米面附近的能带结构有重要的影响。

3.2.3.Mn0.125Mg0.875F2的光学性质

图4 Mn0.125Mg0.875F2不同原子分态密度和总态密度

为了探究Mn0.125Mg0.875F2的光学性质，由所得的能带结构，可以进一步的计算了其介电函数和吸收系数这两个参量。在线性响应范围内，固体的宏观光学响应函数可用复折射率N（ω）=n（ω）+ip（ω）来描述，也可用光的复介电常数ε（ω）=ε1（ω）+iε2（ω）来描述。再根据克拉墨斯—克勒尼希（Kramers-Kroning）色散关系可以推导出晶体介电函数实部，根据计算占据态和非占据态波函数的矩阵元素得到介电函数虚部[18]，其相关公式如下：

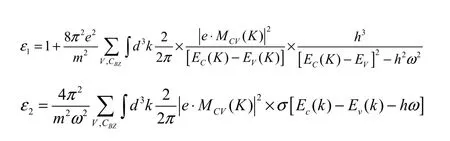
上两式是分析晶体能带结构和光学特性的理论依据。据其计算结果探究MgF2和Mn：MgF2晶体及其相关材料的光学特性。图5中所示为Mn0.125Mg0.875F2的光吸收系数。

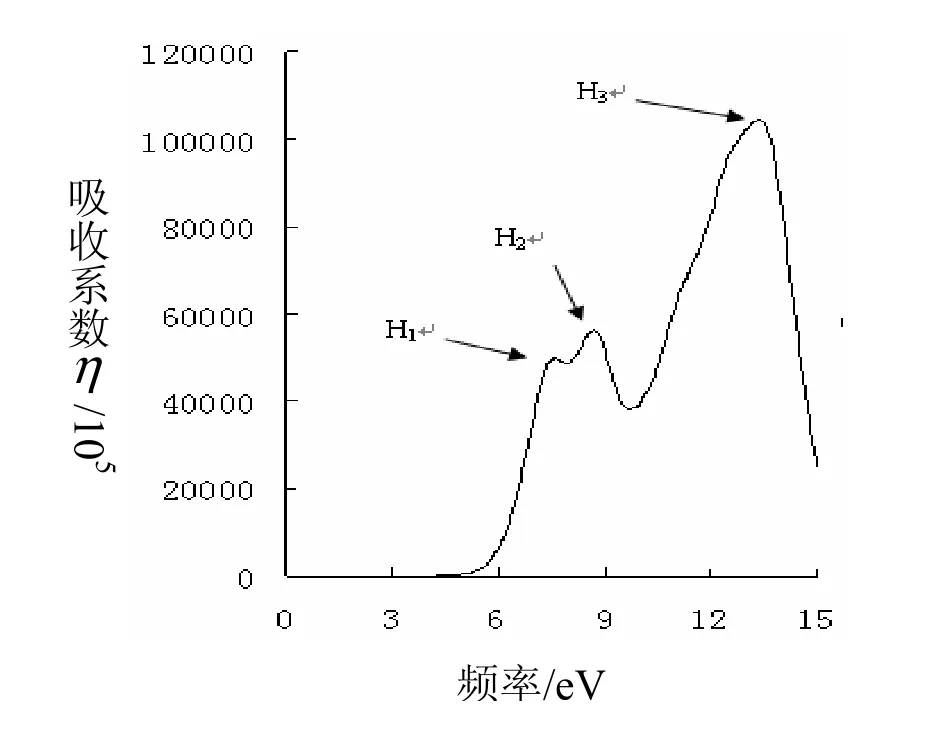
图5图 M5n0.125MMn0g.102.58M75gF0.287的5F2吸的收吸收光光谱

由图5可以看出，其中的三个吸收峰为H1、H2、H3,对应的能量分别为 7.79eV、8.85eV、13.42eV。将其与图3比较可以看出，Mn的掺入，在本征吸收边的左侧附近可能存在一些电子的带内跃迁。一般情况而言，在价带的顶部会存在少量的空穴，可能是由于这些空穴的存在而使部分电子发生带内跃迁，这些带内跃迁也会吸收光子，吸收的光子的能量比禁带宽度小，从而会在本征吸收边的左侧形成新的吸收带。由此可以得出，Mn掺入过后，体系的吸收波峰H1、H2分别对应的Z点导带顶与价带低之间产生的跃迁；H3对应的R点导带顶与价带低之间产生的跃迁。这些说明了，Mn的掺入后对吸收光谱有所调制。

4.结论

基于CASTEP软件和密度泛函理论（DFT）第一性原理平面波超软赝势方法来计算Mn掺杂MgF2晶体的电子结构、几何机构和光学性质。结果表明，经过Mn掺杂MgF2的浓度为12.5%时，MgF2的结构并没有发生明显的结构畸变。但对体系的能带结构，尤其是费米面附近的能带结构有重要的影响。通过计算结果也得出，Mn掺杂过后，吸收光谱和介电常数有所调制，结果与实验测量大致吻合。这些对MgF2和Mn：MgF2的制备以及其相关材料在光学器件方面的运用在理论上提供参考。

[1] Deng C.Y, He D. W, Zang Y. S, Kang X. W. 2004 Chin.Phys. 13：473.

[2] Maria W，Michal Z，Mariusz P，2003 J.Fluorine Chemistry 120：1.

[3] Wevers M.A.C， Schon J.C， Jansen M 2001 J.phys. A：Math.Gen.34：4041.

[4] Barker A.S，1964 J.phys.Rev.136：A1290.

[5] Rao J.L，Krishma R.M，Lakshman S.V.1987 Phys.Stat.Sol. （b） 143：K99.

[6] Remme S，Lehmann G.，Recker et al 1985 Solid State Commun.56：73.

[7] Zhao M.G. 1998 Chin.Phys.Lett.15：43.

[8] Xie L.H，Qiu M.Acta.Phys.Sin.2005，54：5845 （in Chinese）[谢林华、丘 岷 2005 物理学报 54：5845].

[9] Vidal-Valat J.P.，Zenyen M.E，Kurrkisuonio K.1979 Acta.Crystallogr.Sect.B 35：1584.

[10] Segall M.D，Lindan J.D.P.，Probert M.J.，Pickard C.J，Hasnip P.J，Clark S.J.，Payne M.C.，2002 J.Phy.Condens.Matter.14：2717.

[11] Payne M.C，Teter M.P.，Allan D.C.1992 Rev.Mod.Phys. 64：1045.

[12] Vanderbilt D.1990 Phys.Rev.B 41：7892.

[13] Zhu S.L.2008Atomic Physics（Beijing：Higher Education Press）：206-208（in Chinese）[褚圣麟2008原子物理学（北京：高等教育出版社）：206-208].

[14] Zhang J.H.，Ding J.W.，Lu Z.H.2009Acta.Phy.Sin.07：1901（in Chinese）[张计划、丁建文、卢章辉 2009 物理学报07 ：1901].

[15] Simanovskii D.M.，Schwettman H.A.2003 Phys.Rev.Lett. 91：107601.

[16] Xu L.，Tang C.Q.，Dai L.，Tang D.H.，Ma X.G.，2007 Acta.Phys.Sin.56：1048（in Chinese）[徐 凌、唐超群、戴 磊、唐代海、马新国 2007 物理学报 56：1048].

[17] Osuch K.，Lombardi E.B.，Gebicki W.2006 Phys.Rev.B.73：75202.

[18] Shen X.C.1992 The Sceptrum and Optical of Semiconductor（Beijing：Science Press）：76（in Chinese）[沈学础.半导体光谱和光学性质（第2版）[M].北京：科学出版社，1992：76].

The Research on the First Principle of Optical Properties ofMnDoped2
MgF

JIA Mu1, LONG Shao-tang2
（ 1. School of Mechanical Engineering, Shandong University; Shandong Jinan 250100, China;
2. Department of Physics and Electronic Science, Tongren University; Tongren, Guizhou 554300, China ）

The plane wave pseudopotential method, based on the first principle of DFT, is applied in the calculation of geometry, electron structure, and optical properties of the crystalloid doped by Mn. Results show that system structure has no obvious structure deformity or change when the doping density is 12.5%. However, there exist significant influences on the system band structure, especially the band structure around Fermi surface. With modulation on absorption spectra and dielectric constant, results are in good agreement with the experimental measurements.

MgF2;doping;electron structure;optical properties;the first principle

（责任编辑 李宗宝）

K28 < class="emphasis_bold">文献标识码：A

A

1673-9639 （2011） 03-0117-04

2011-03-24

贾牧，男，山东大学机械工程学院教师。