一类抛物型方程的有限差分法

刘相国，徐富强

（ 巢湖学院 数学系，安徽 巢湖 238000 ）

一类抛物型方程的有限差分法

刘相国，徐富强

（ 巢湖学院 数学系，安徽 巢湖 238000 ）

利用有限差分法求解了抛物型方程边值问题，得到了相应的稳定性分析，并进行了数值模拟。模拟结果表明该方法是可行的、有效的。

抛物型方程； 有限差分法； 稳定性

现代科学、技术、工程中的大量数学模型都可用偏微分方程来描述，很多近代自然科学的基本方程本身就是偏微分方程。人们一直用微分方程来描述、解释遇见的各种自然现象，但绝大部分偏微分方程的定解不能以实用的解析形式来表示，这就给一些自然现象的定量描述带来了很大的困难。随着计算机的出现和发展，一门新兴的学科——微分方程的数值[1][2][3]方法得到了前所未有的发展和应用，并形成了一个专门的数学分支，成为理论和应用研究的热点课题。本文利用有限差分法研究了热传导方程边值问题，[4]并进行了稳定性分析[5][6][7]和相应的数值模拟，取得了较满意的数值试验结果。

1.数学模型

设一类最简单的抛物型方程——热传导方程，表示为：

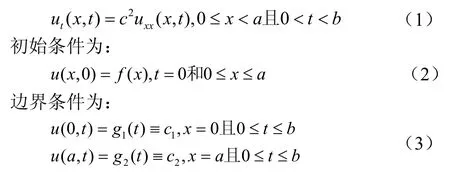
热传导方程是初始温度分布函数为f（x），端点有恒温c1和c2的绝缘杆上温度的数学模型。尽管通过傅里叶级数可得到方程的解析解，但这里将它作为求解抛物型方程数值解的一个原型。

1.1. 向前差分法

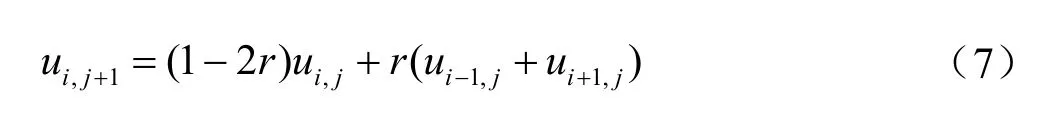
设行j的近似值已知，通过式（7）可得到网格中的行j+1的近似值。注意此公式是根据ui−1,j、ui,j和

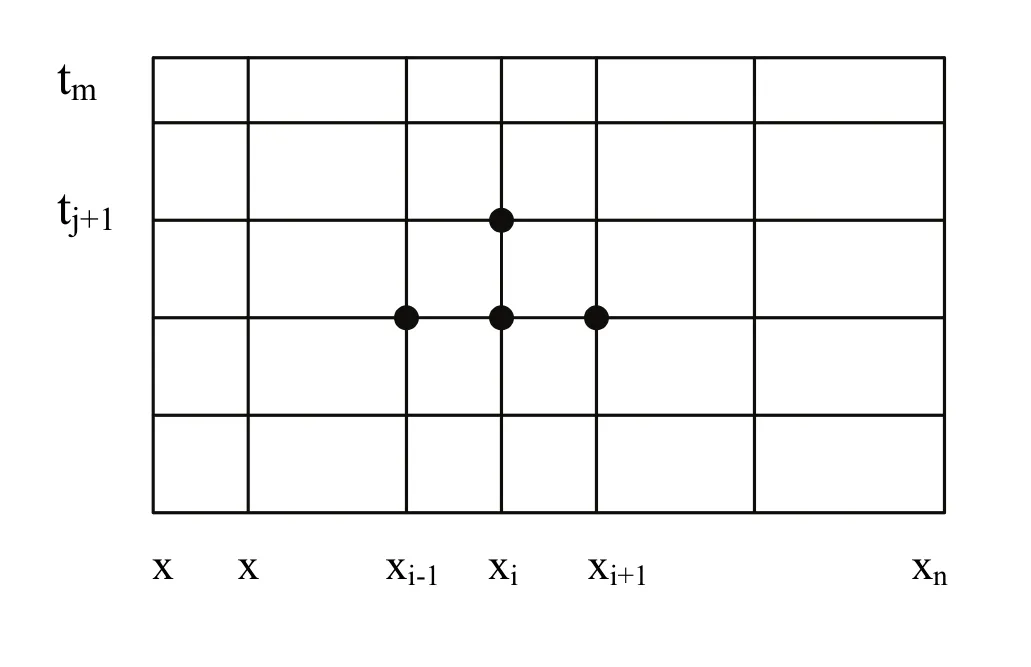
图1 在区间R内求解ut（x,t ）=c2uxx（x,t）网格

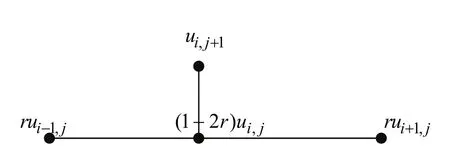
图2：向前差分空格样板

差分方程（7）的精度为O（k）+O（h2）。因为项O（k）随着k趋近于零而线性减小，所以使它的值小可得到更好的近似值。然而，稳定性需求需要考虑更多。设网格的解精度不够，而且Δx=h0和Δt=k0必须减小。为简单起见，设新的x增量为Δx=h1=h0/2。如果采用同样的r，则k1必须满足：

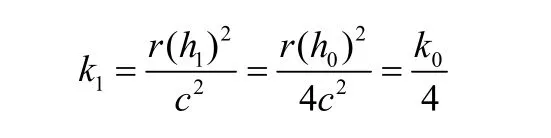
这使得沿x轴和t轴的网格点的数量分别增加到2倍和4倍。这样当减少网格大小时，会增加8倍的计算量。这样的努力是不提倡的，需要开发更有效的无稳定性限制的方法。通过增加方法的复杂性可达到所需的无条件稳定性。

（二）Crank-Nicholson法

由John Crank和Phyllis Nicholson发明的隐式差分格式是基于求解网格中在行之间点（x,t+k/2）处的式（1）的数值近似解。而且求解ut（x,t+k2）的近似值公式是从中心差分方程中得到，表示为：

其中i=2,3,…,n−1。式（15）右边的项都是已知的。因此，式（15）可形成对角线性方程组AX=B。式（15）中使用了 6个点，并结合了数值差分基于的中间网格点，如图3所示，有时通过使r=1来实现式（15）。在这种情况下，沿t轴的增量为Δt=k=h2/c2，同时式（15）可简化为：

当Crank-Nicholson法用计算机实现时，可通过直接解法或迭代法得到线性方程组AX=B。

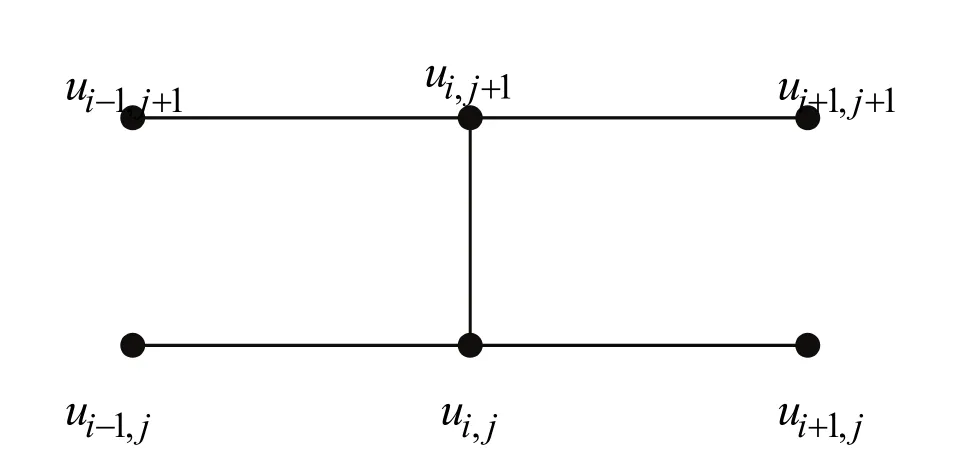
图3：Crank-Nicholson法的空格样板

2.稳定性研究

抛物型方程的差分格式在实际应用时，都取逐层计算的形式。当初始层上的解有误差时，必须逐层传播，影响以后各层的解，研究这个误差传播的规律是稳定性讨论的任务。下面以齐次边界条件热传导方程（1）、（2）、（3）的差分格式为模型，进行叙述和讨论：

3.数值算例

用向前差分法以及C-N格式求解热传导方程：

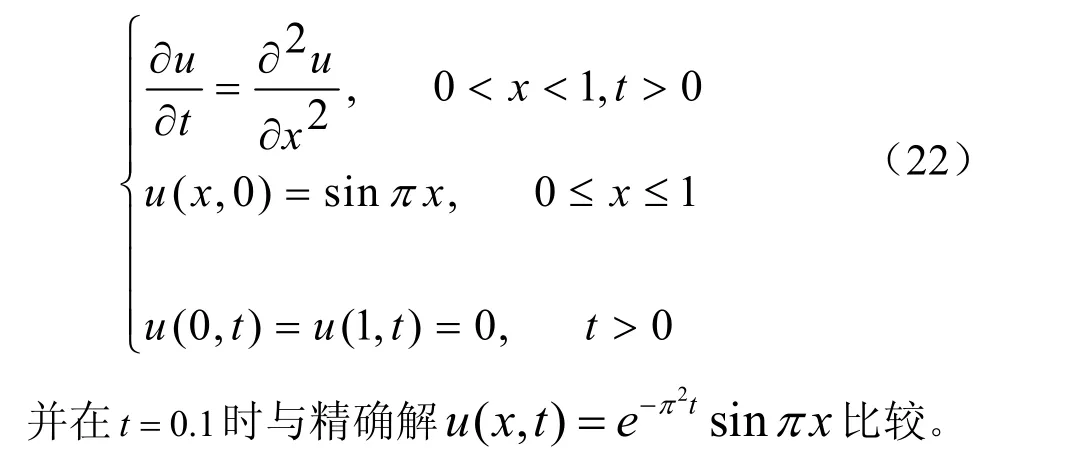
例1用向前差分法求解（22）如下：

（1）当r=0.1、t=0.1、h=0.1（m=10、N=100）时取部分节点上的运行结果（表1）及数值解剖分图（图4）如下：

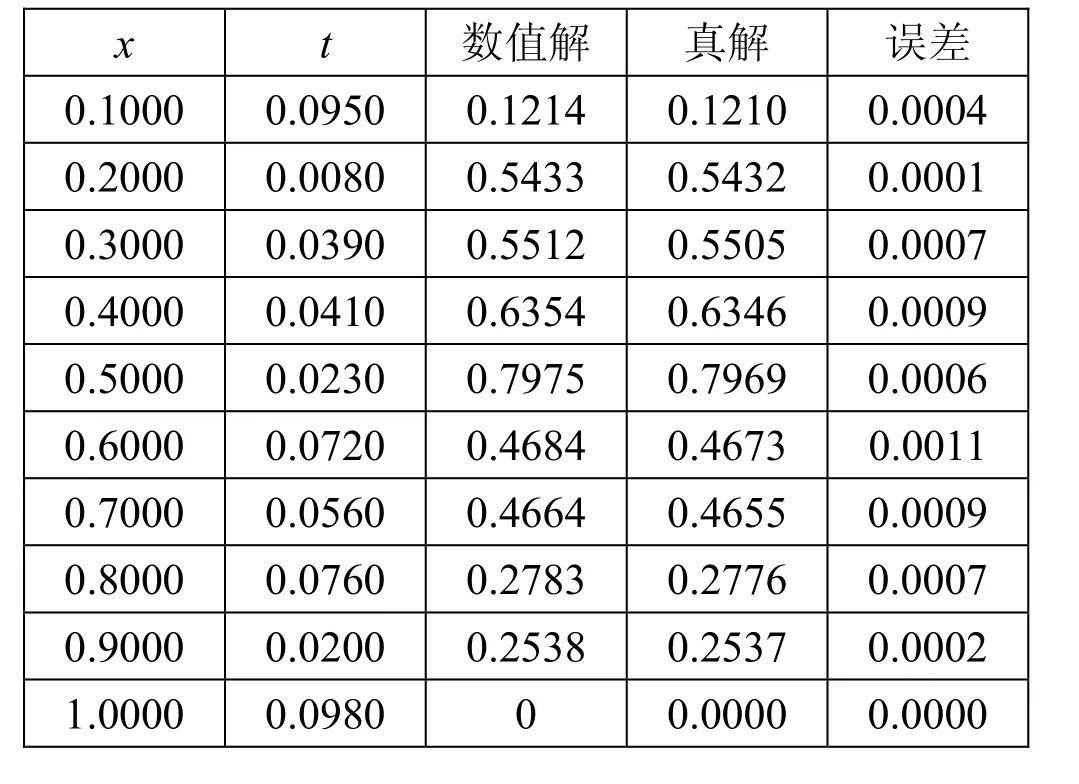
表 1 当r=0.1、t=0.1、h=0.1（m=10、N=100）时部分节点上的运行结果

（2）当r=0.5、t=0.1、h=0.1（m=10、N=20）时取部分节点上的运行结果（表2）及数值解剖分图（图5）如下：

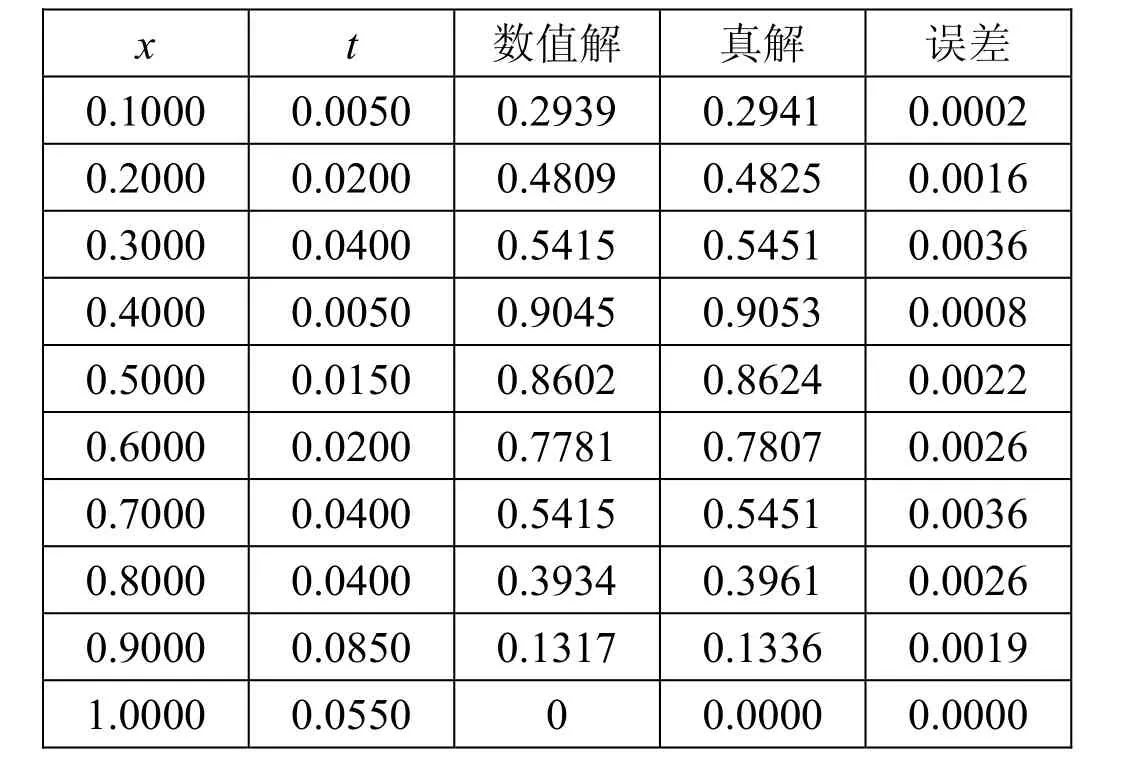
表2 当r=0.5、t=0.1、h=0.1（m=10、N=20）时部分节点上的运行结果

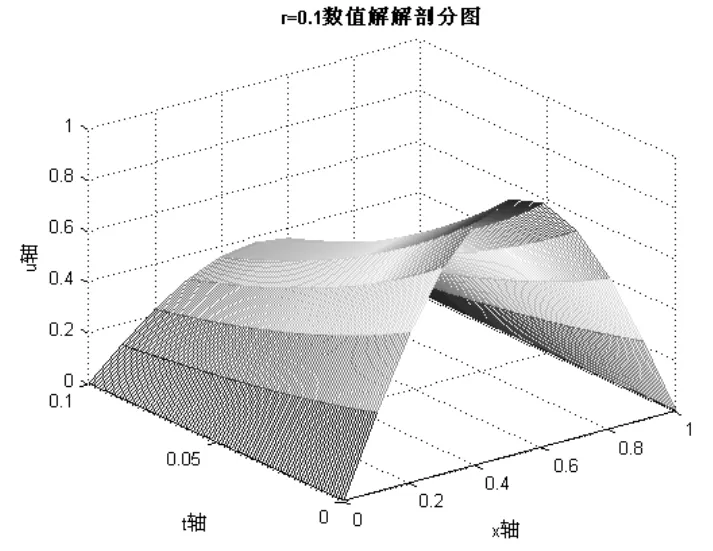
图4 数值解剖分图

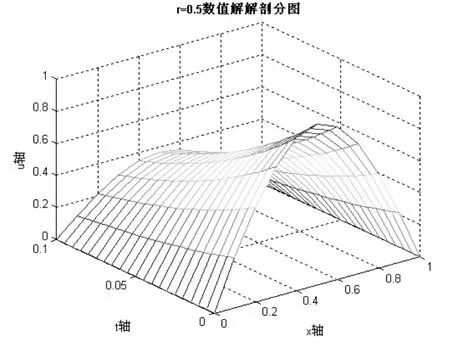
图5 数值解剖分图

例2用Crank-Nicholson法求解（22）如下：

<1>当r=0.1、t=0.1、h=0.1（m=10、N=100）时，取部分节点上的运行结果，见表3。

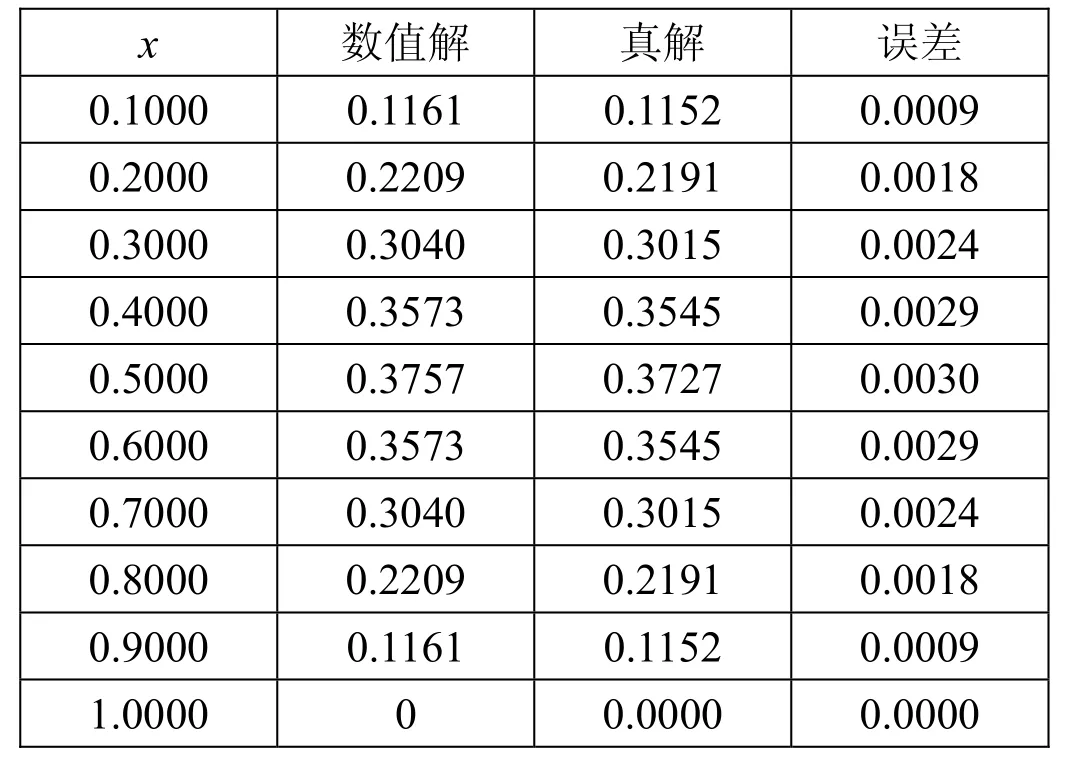
表 3 当r=0.1、t=0.1、h=0.1（m=10、N=100）时部分节点上的运行结果

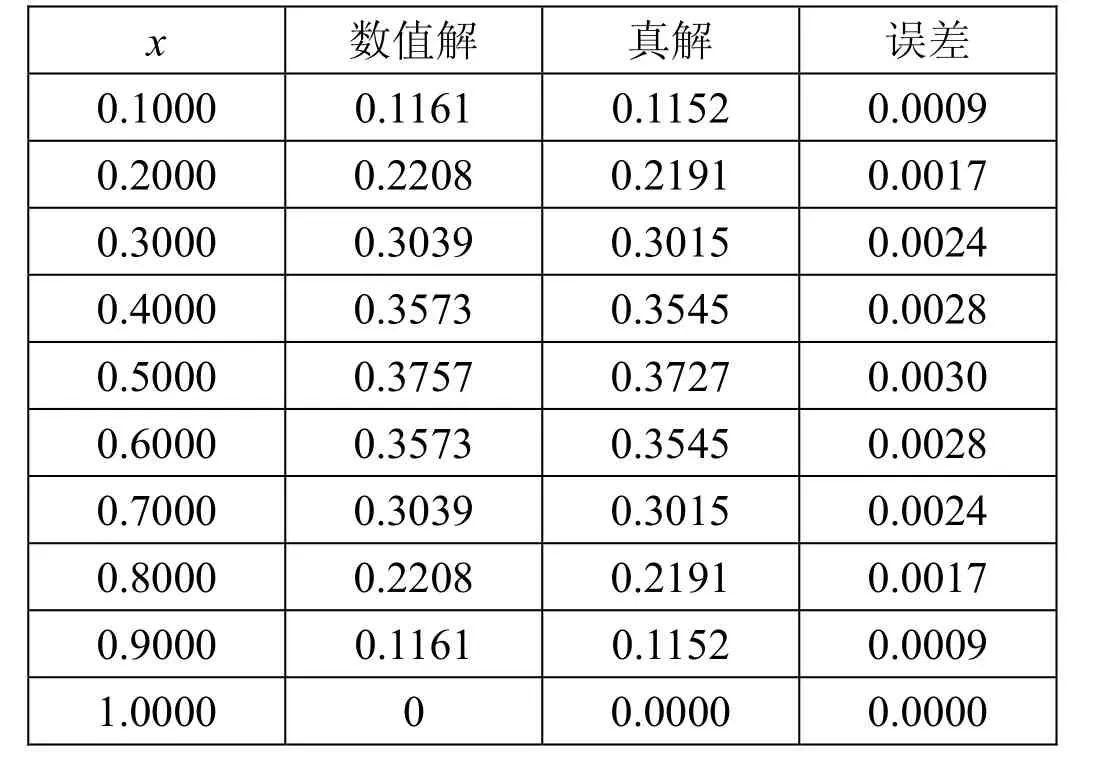
表4 当r=0.5、t=0.1、h=0.1（m=10、N=100）时部分节点上的运行结果

4.结论

本文利用有限差分法研究了一类抛物型偏微分方程边值问题，并建立了相应的稳定性分析。通过数值模拟可以看出，有限差分法在求解此类问题是有效性和可行的。并且该法求得的数值解有较高的精度。

[1] Carlos Castro, Sorin Micu. Boundary controllability of a linear semi-discrete 1-D wave equation derived from a mixed finite element method[J]. Numer. Math. （2006） 102：413–462.

[2] Partha Roy Chaudhuri. Sourabh Roy. Analysis of arbitrary index profile planar optical waveguides and multilayer nonlinear structures： a simple finite difference algorithm[J].Opt. Quant. Electron. （2007） 39： 221–237.

[3] LUO Yun-ju, LIU Dong-yan, LIU Xin-rong. Finite element numerical simulation for the hydrodynamic field evolution of geothermal water in the nanwenquan anticline in chongqing in china[J]. Journal of Hydrodynamics, 2006,18（4）： 443-448.

[4] 周顺兴.解抛物型偏分方程的高精度差分格式[J].计算数学，1982，4（2）：204-203.

[5] 金承日.解抛物型方程的高精度显式差分格式[J].计算数学，1991，（1）： 38-44.

[6] 李荣华.偏微分方程数值解法[M].北京：高等教育出版社，2005.

[7] 范德辉等.对流扩散方程差分格式稳定性分析[J].暨南大学学报（自然科学版），2006，27（1）：24-29.

A Finite Difference Method for Solving Parabolic Equation

LIU Xiang-guo, XU Fu-qiang
（ Department of Mathematics, Chaohu University, Chaohu, Anhui 238000, China ）

This paper uses finite difference method to solve the boundary value problem of parabolic equation,obtaining the corresponding stability analysis and numerical simulation. Simulation results show that the method is feasible and effective.

parabolic equation;finite difference;stability

（责任编辑 李宗宝）

H319 < class="emphasis_bold">文献标识码：A

A

1673-9639 （2011） 04-0139-05

2011-01-03

巢湖学院科研基金项目（编号：XLY-201006）。

刘相国（1979-），男，宁夏人，巢湖学院数学系教师。

徐富强（1984-），安徽宣城人，研究方向：智能计算。