数理模型下抵押贷款共同保险的Martingale评价

李 晨，李小春

（ 湖南农业大学 东方科技学院，湖南 长沙 410128 ）

数理模型下抵押贷款共同保险的Martingale评价

李 晨，李小春

（ 湖南农业大学 东方科技学院，湖南 长沙 410128 ）

假设未偿付额可由风险信用评估得到，房产价格服从一般It过程，构建了抵押贷款共同保险的数理评价模型，利用Martingale评价方法，得到了房屋抵押贷款共同保险的精确定价公式。

抵押贷款； 保险； Martingale评价

1.引言

住房抵押贷款这一金融业务现在已经非常普及，数量巨大，但其间也存在着巨大的风险, 如贷款条件风险、住房毁损风险、债务人信用风险、抵押物处理风险等。美国次级抵押贷款危机就是一个很好的警示。有风险就有保险的必要。风险愈大，保险开发和发展的可能性就越大。然而，我国住房抵押贷款保险的现状是发展滞后，险种单一，并且因地而异，远远不能满足我国的实际需要。现实生活中，不同的购房者有不同资信状况和经济实力，多样化的险种有利于银行和购房者做出灵活的决策。因此，有必要推出新的抵押贷款险种，或者在原有险种的基础上进行创新，使之更符合广大购房者的实际情况。[1][2][3][4][5][6]

本文借鉴国外保险经验，基于部分担保保证险，提出了如下抵押贷款共同保险的新概念。若贷款机构最终的损失额低于保险机构的第一赔付限额k1A0，则由保险公司取得房产权，并向贷款机构支付全部未偿贷款余额。此时，贷款机构所持有的共同保险保单可获得的赔付额为max（UH（T）−αPH（T）,0）。此处，A0表示原始贷款本金，UH（T）表示T时刻的未偿付金额，PH（T）表示T时刻的房产价格,表示保险公司实现房屋抵押权后所得的住房价值比例。超过这一赔付限额k1A0的部分，则按照一定的比例k2在保险公司和贷款机构之间分配损失额。因此我们不妨称这种保险为房屋抵押贷款共同保险。

贷款机构持有的这种抵押贷款共同保险保单到期收益为：

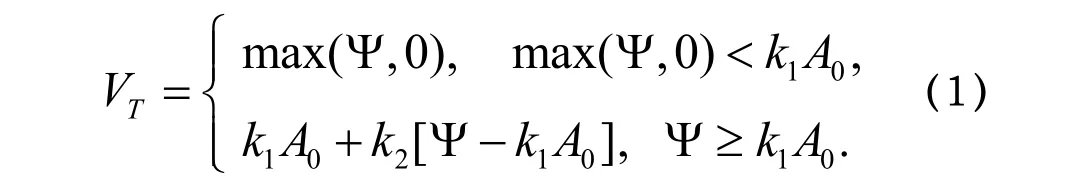
其中Ψ=UH（T）−αPH（T）.

2.共同保险评价模型的构建

给定某完备概率空间（Ω,F,Ρ），到期日用t=T表示，现在时刻用t=0表示，无风险利率用时间t的函数r（t）表示，t时刻的未偿付额用UH（t）表示。未偿付额UH（T）可以由风险信用评估得到，因此不妨设它为常数UH。房产价格PH（t）是定义在完备概率空间（Ω,F,Ρ）上的随机变量，且满足如下随机微分方程：

3.Martingale评价方法在求解共同保险评价模型中的应用

Martingale评价方法（又称为概率平赌评价方法）最早由Cox及Ross于1976年提出，主要用于对衍生性商品进行评价。在Martingale评价方法下，一种证券（或衍生性商品）的价格可通过对该证券未来的期望现金流进行贴现得到，且期望值贴现可在风险中性下进行。和评价衍生性商品的另一种常见方法——解偏微分方程相比，Martingale评价方法更简单，且很少涉及复杂的积分。许多偏微分方程式不能求解的问题，经由Martingale评价方法都可迎刃而解。

由Martingale评价方法，抵押贷款共同保险在现在时刻的价值为：

[1] 侯新华，田策.住房抵押贷款保证险研究[J].中国房地产金融，2002，（11）：11-13.

[2] 钱乃余.发展我国住房抵押贷款保险之构想[J].济南金融，2001，（6），37-38.

[3] 陈丽萍，杨向群.房价服从非时齐Poisson跳扩散的住房抵押贷款保证险的定价[J].应用概率统计，2007，23（4）：345-351.

[4] 李晨，陈丽萍，杨向群.随机波动率与跳扩散相结合的保证险的鞅定价[J].系统工程，2009，27（3）：41-45.

[5] Bladt M T, Rydberg H..An actuarial approach to option pricing under the physical measure and without market assumption[J].Insurance： Mathematics and Economics,1998, 22（1）： 65-73.

[6] 李晨，陈丽萍.指数O-U过程下保证险的保险精算定价[J].数学的实践与认识，2009，39（4）：21-26.

Pricing Mortgage Insurance with the Method of Martingale

LI Chen, LI Xiao-chun
（ Orient Science & Technology College, Hunan Agricultural University, Changsha, Hunan 410128, China ）

Under the assumptions that the unpaid money is a constant and the house price is driven by an Ito^process, introducing the Martingale Pricing Method, we obtain the pricing formulas of the mortgage insurance.

mortgage;insurance;Martingale pricing

（责任编辑 毛志）

F830.9；O211.6 < class="emphasis_bold">文献标识码：A

A

1673-9639 （2011） 04-0057-03

2011-06-26

国家自然科学基金资助（10871064）。

李 晨（1979-），男，湖南益阳人，讲师, 硕士，研究方向：数理金融学。

李小春（1979-），男，湖南邵阳人，讲师，硕士，研究方向：分形几何及生物信息学。