A356合金疲劳数据的数理统计分析

宋谋胜，晏登扬

（ 铜仁学院 物理与电子科学系，贵州 铜仁 554300 ）

A356合金疲劳数据的数理统计分析

宋谋胜，晏登扬

（ 铜仁学院 物理与电子科学系，贵州 铜仁 554300 ）

研究了不同加钛方式和钛含量对A356合金低周疲劳性能的影响，并重点对实验数据进行了数理统计分析，拟合了四种合金的Manson-Confin方程，分析了实验数据的统计可靠性与显著性。结果表明，A356合金低周疲劳寿命对加钛方式不敏感，其疲劳寿命仅受合金中Ti含量影响。无论电解加钛合金还是熔配加钛合金，Ti含量为0.1%的合金较0.14%的合金具有更优异的低周疲劳性能。

A356合金； 疲劳寿命； 拟合； 数理统计

材料的疲劳是指材料在应力或应变的交变作用下所发生的性能变化，一般情况下特指那些导致开裂或断裂的性能变化[1][2]。实际上，疲劳断裂一直是机械零件和工程构件破坏的最主要形式，在航空航天、化工机械、交通运输、工程机械等领域中，约有50%～90%的结构强度破坏是由疲劳破坏造成的。由于绝大部分工程结构材料在实际服役期间承受的是交变载荷，疲劳破坏成为了构件失效的主要形式，也是影响构件服役寿命的重要因素。在交变载荷下，应力集中部位的材料循环塑性变形行为对构件的疲劳服役性能起决定性影响[3][4]，因此研究材料在应变控制条件下的低周疲劳性能极具实际意义。然而，通常材料的疲劳测试是一项非常耗时耗财的繁重任务，需要投入大量的人力、物力，且所得的实验数据极为庞杂而分散，具有很大的随机分布性。但大量研究表明，在同一应变水平上，试样对数疲劳寿命统计分布呈正态分布规律[5]。因此，在材料的低周疲劳测试中，有必要对非常分散、相差较大的实验数据进行数理统计方面的分析，从而在设计选材、优化性能、疲劳寿命预测等方面获得更多的信息，最大效果地发挥材料的潜能。

A356合金因具有优良的铸造性能、热处理性能、加工性能、疲劳性能以及良好的强度与塑性而被广泛地使用在汽车、摩托车轮毂等产业中[6][7]。目前，人们对A356合金的常规力学性能研究较多，而对其疲劳性能的研究相对有限。本实验分别采用电解加钛和熔配加钛两种方式配制了两种 Ti含量的 A356合金，在对其低周疲劳性能进行测试基础上，利用数理统计的方法对测试数据进行了分析。

1.实验材料与方法

实验材料为两种Ti含量（0.10%, 0.14%）的电解加钛A356合金（E10, E14）和熔配加钛A356合金（M10, M14）。电解加钛 A356合金直接采用 Ti含量为0.18%的电解低钛铝合金熔配而成，熔配加钛A356合金则采用 Al-5%Ti中间合金和纯铝熔配而成，四种实验合金的化学成分见表1。浇注的试样经T6热处理后加工成标准的疲劳测试试样（φ8× 16），然后在MTS-810液压伺服材料试验机上进行低周疲劳测试。疲劳实验名义总应变半幅分别取Δε2=0.9× 10−2,0.7× 10−2,0.5× 10−2,0.3× 10−2,0.25× 10−2

t共5个幅值，应变比R=−1。最后对疲劳实验数据进行数理统计分析。

表1 A356合金的化学成分 （wt.%）Tab. 1 Chemical compositions of A356 alloys

2.实验结果分析

2.1. A356合金的低周疲劳寿命

在低周疲劳测试中，由于材料的应力应变已超过其弹性范围而进入塑性区，因此实验中的总应变半幅（Δt2）由弹性应变半幅（Δe2）和塑性应变半幅（Δp2）组成。材料的循环应变―疲劳寿命（Δε−Nf）关系是衡量和评估材料疲劳服役性能、预测材料疲劳寿命的重要参量。低周疲劳的Δε−Nf关系通常采用总应变半幅（Δt2）和循环反向次数（2Nf）在双对数坐标上表示，即Δεt2−2Nf曲线。同理，Δεe2−2Nf和Δεp2−2Nf关系也可在双对数坐标上表示。

图 1显示出了 Ti含量分别为 0.1%和 0.14%的A356合金在电解加钛和熔配加钛两种方式下的循环Δt2−2Nf、Δe2−2Nf、Δp2−2Nf关系曲线。可见，无论是电解加钛还是熔配加钛，Ti含量为0.1%的A356合金低周疲劳寿命要优于Ti含量为0.14%的A356合金低周疲劳寿命，表明前者具有更好的抗低周疲劳性能。还可以看出，弹性应变对A356合金低周疲劳寿命的影响不明显，而塑性应变的影响则较为明显，因此材料的低周疲劳寿命主要取决于材料的塑性应变。

图1 A356合金的循环应变―寿命曲线：（a）电解加钛，（b）熔配加钛Fig. 1 Cyclic Δ2−2Nf plots of A356 alloys

图2显示出了相同Ti含量下加钛方式对材料疲劳寿命的影响。很明显，在相同Ti含量下，两种加钛方式合金具有极为相近的低周疲劳寿命，表明A356合金的疲劳寿命对加钛方式的影响不敏感。当Ti含量为0.1%时，熔配加钛合金的低周疲劳寿命在高应变幅下略高于电解加钛合金的。这是因为后者是采用钛含量为0.1%的A356锭重熔而具有较粗的组织，使得疲劳性能略低，而在低应变幅下二者的疲劳寿命相当。当钛含量为0.14%时，两种加钛方式合金的疲劳寿命一直保持相当。这说明实验合金在相同的Ti含量下具有相近的循环疲劳强度与循环疲劳塑性，从而显示相当的疲劳寿命。

图2 A356合金的循环总应变―寿命曲线：（a）0.1%Ti，（b）0.14%TiFig. 2 Cyclic Δεt 2−2Nf plots of A356 alloys

2.2. 实验数据的数理统计分析

通常，金属材料的低周疲劳寿命Δε2−2Nf关系可用Manson-Coffin方程描述[8]：

对（5）式进行最大似然处理，可以得出A、B的最大似然估计值为：

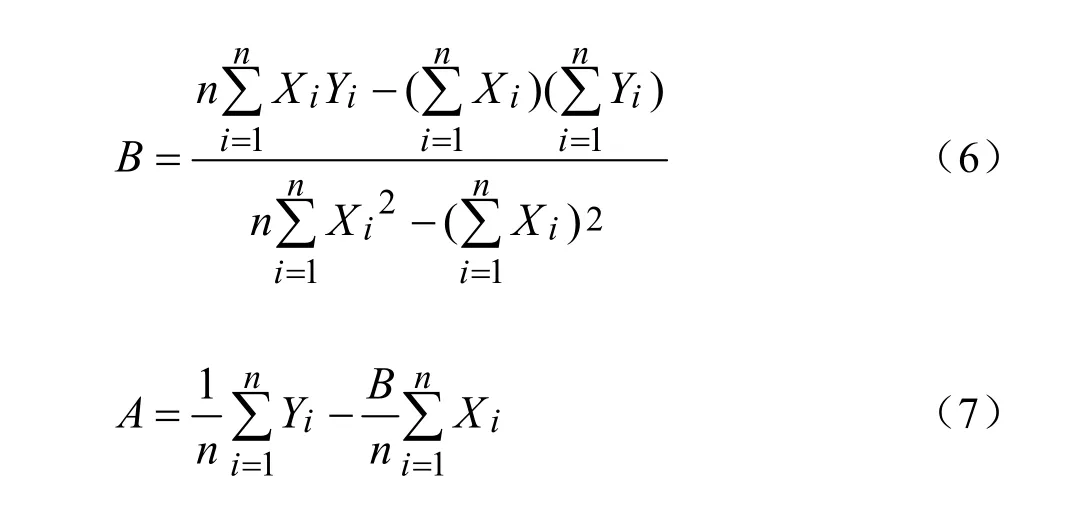
将A、B之值代入（4）式所得的方程则为Y关于X的线性回归方程。

利用实验的原始数据来计算出相应的X、Y值并将其代入A、B似然估计公式中，经整理后得：

得：XY=−99.8%，|XY|较大，它表明X，Y的线性相关程度非常好。

同理可拟合出 E10、E14、M10和 M14合金相应b，c，′f，′f值，结果如表2示。由表2可见，E14、M14及E10、M10合金的疲劳强度指数b、疲劳强度系数′f相当，表明电解加钛和熔配加钛合金

从而有：c=−0.63，′f=24%=0.24。另由X，Y的相关系数公式：的强度相当，弹性应变对材料所造成的疲劳损伤相当，而两种加钛方式合金的疲劳塑性指数 c、疲劳塑性系数′f也相近，表明二者的塑性相近，塑性应变对材料所造成的疲劳损伤相近，因此两种加钛方式合金的疲劳寿命也相近。但是钛含量为0.10%的合金却具有较大的疲劳塑性指数c和疲劳塑性系数′f，较低的疲劳强度指数b和疲劳强度系数′f，这使得其在疲劳服役过程中更能缓解由于材料的塑性变形所造成的疲劳损伤，从而具有较好的低周疲劳性能。

表2 Manson-Coffin方程的参数Tab. 2 Parameters of Manson-Coffin equation

实验时取n=5, =10%，将疲劳寿命数据代入（9）、（10）式，在t分布表中查出相应的值，从而计算出的值，μ、2Nf的置信区间，如表 3所示。

另外，由（9）式得：

在实验中，因测试数据分散性较大，一般取=α10%， =5%。现以E10的Δεt/2=0.9%为例，代入数据，得n0=4.5，而实验时试样个数n=5，因此实验数据应为可靠。

另外，还可考查合金间疲劳寿命的差异性，即材料的显著性。因疲劳对数寿命服从正态分布，即N（μ,2），其中μ为样品均值，σ2为样本方差。对于X，Y两组独立随机变量，设x1,x2,....,xn是来自X样本值，y1,y2,....,yn是来自Y样本值，这两组数据总是成对出现。另设Z为这两组数据之差，即Z=Y−X，z1,z2,....,zn是来自Z样本值，则Z也满足正态分布，于是有统计量：

表3 A356合金低周疲劳寿命的置信区间Tab. 3 Reliability region of LCF life for A356 alloys

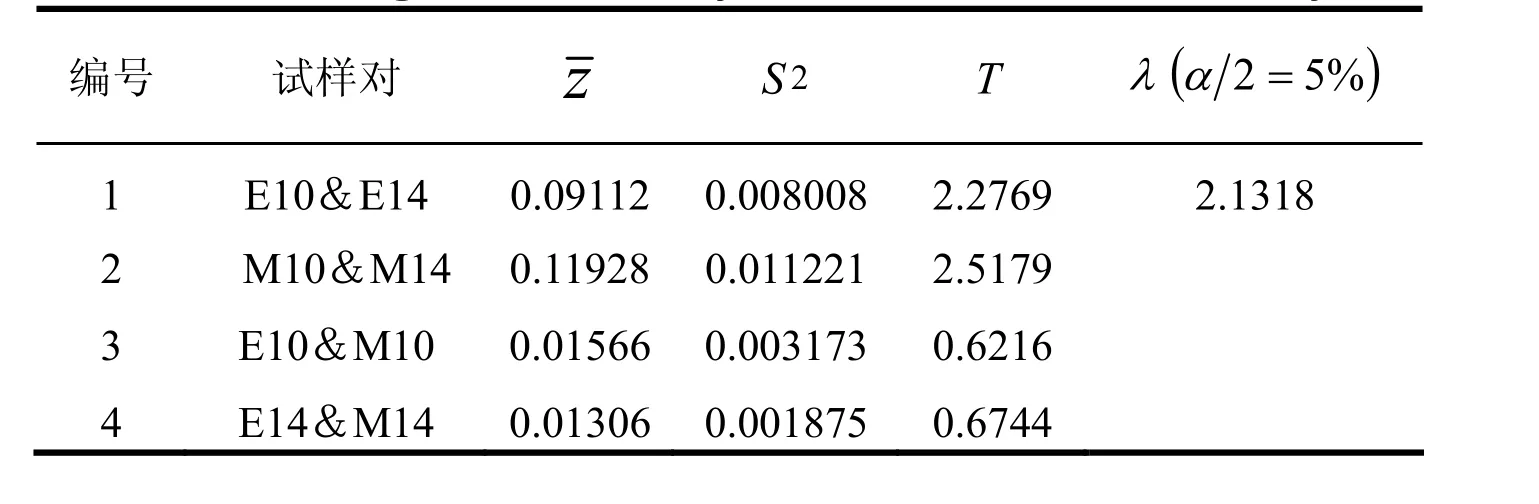
表4 A356合金疲劳寿命的显著性分析Tab. 4 Significance analysis of LCF life for A356 alloys

3.结论

对 A356合金低周疲劳实验数据的数理统计分析表明，加钛方式对 A356合金低周疲劳寿命的影响不明显，而Ti含量对低周疲劳寿命影响较大。无论是电解加钛合金还是熔配加钛合金，Ti含量为0.1%的 A356合金低周疲劳性能要优于 Ti含量为0.14%的。

[1] （美） Suresh S.材料的疲劳[M].王光中等，译.北京：国防工业出版社，第2版，1999，5.

[2] Murakami Y, Miller K J. What is fatigue damage? A view point from the observation of low cycle fatigue process[J].Int J Fatigue, 2005, 27（8）： 991-1005.

[3] Jian Y Y, Ott W, Baum C. Fatigue life predictions by integrating EVICD fatigue damage model and an advanced cyclic plasticity theory [J]. Int J Plast, 2009, 25（5）： 780-801.

[4] Emami A R, Begum S, Chen D L. Cyclic deformation behavior of a cast aluminum alloy [J]. Mater Sci Eng A, 2009,516（1-2）： 31-41.

[5] Goswami T. Low cycle fatigue life prediction, a new model[J]. Int J Fatigue, 1997, 19（2）： 109-115.

[6] Miller W S, Zhuang L, Bottema J. Recent development in aluminium alloys for the automotive industry[J]. Mater Sci Eng A, 2000, 280： 37-49.

[7] 宋谋胜，冉茂武，孔园园等.A356合金低周疲劳性能及其可靠性研究[J].铸造技术，2010，31（6）：735-739.

[8] Alush H, Katz Y, Maros M B. Some insights into the remote strain versus fatigue life relationship [J]. J Mater Process Technol, 2004, 157-158： 16-22.

[9] 刘瑞堂，刘文博.工程材料力学性能[M].哈尔滨：哈尔滨工业大学出版社，2001，8.

Mathematical Statistics Analysis of Fatigue Data for A356 Alloys

SONG Mou-sheng, YAN Deng-yang
（ Department of Physics and Electronics Science, Tongren University, Tongren 554300, China ）

The effects of Ti-addition methods and Ti contents on the low-cycle fatigue （LCF） properties of A356 alloys were investigated, as well as the mathematical statistics analysis of the experimental data of four alloys was chiefly performed, including their fittings of Manson-Confin equations and the analysis of statistics reliability and significance. It is found that the LCF life of A356 alloys is insensitive to the Ti-addition method, and is only influenced by the Ti content in the alloys. Whether added by electrolysis or by melting Al-Ti master alloy, A356 alloys with 0.1%Ti content exhibited the better LCF properties in comparion to those of A356 alloys with 0.14%Ti content.

A356 alloys;fatigue life;fitting;mathematical statistics

（责任编辑 毛志）

TG146.2 < class="emphasis_bold">文献标识码：A

A

1673-9639 （2011） 04-0133-06

2011-05-03

贵州省科学技术基金项目（J20102016），铜仁学院科研基金项目（TR084）。

宋谋胜（1972-），男，湖南怀化人，博士，副教授，研究方向：材料的强化和韧化。