基于虚拟连接点模型的机载LiDAR系统安置误差自检校
2011-01-04江万寿
张 靖,江万寿
武汉大学测绘遥感信息工程国家重点实验室,湖北武汉430079
基于虚拟连接点模型的机载LiDAR系统安置误差自检校
张 靖,江万寿
武汉大学测绘遥感信息工程国家重点实验室,湖北武汉430079
利用激光扫描直接定位的严格模型,分析LiDAR系统安置误差对定位精度的影响,并设计一种安置参数自检校方法。由于离散采样的激光点之间不存在真实的同名连接点,提出虚拟连接点模型,将虚拟连接点与真实激光点联系起来,并定义两组规则从激光点坐标计算出连接点坐标。采用安阳市内真实LiDAR数据进行试验,证明本文方法的可行性和有效性,自检校获得的安置参数稳定有效,可直接对原始LiDAR条带进行纠正,补偿系统安置误差。
LiDAR;自检校;安置误差;杆臂偏移;视准轴偏角;虚拟连接点模型
1 引 言
机载LiDAR(light detection and ranging)是一种快速采集三维信息的新型遥感技术,在国土测绘、资源勘查、灾害监测等领域都有着广泛的应用前景。典型的机载LiDAR系统包括激光扫描仪,差分GPS接收机和惯性导航单元(IMU)三个主要部分[1]。作为一种多传感器集成系统,LiDAR数据精度不仅受激光测距精度、DGPS定位精度以及IMU定姿精度等因素影响,还受传感器集成时各传感器之间对准精度的影响。LiDAR系统在安装时,GPS天线中心与激光扫描中心的不重合称为杆臂偏移,扫描框架与IMU框架之间的偏角称为视准轴偏角。将杆臂偏移和视准轴偏角这类由传感器未对准造成的误差统称为系统安置误差。与LiDAR系统其他误差源相比,安置误差在系统安装、拆卸过程中都可能发生变化,因此需要经常性地进行安置误差检校[2-3]。
近年来,如何消除LiDAR数据中的系统误差,提高激光点定位精度,一直是研究热点。现有的处理方法可以分成两类:一类是数据驱动方法(通常称为条带平差),另一类是模型驱动方法(通常称为系统检校)[4]。
由于LiDAR系统的各种误差会造成扫描条带之间不重合,条带平差通过选择合适的数学模型对LiDAR条带数据进行变换和改正,使变换后的LiDAR条带之间或LiDAR与实际控制数据之间的偏差最小。具代表性的如文献[5]提出的3参数模型;文献[6]提出的12参数模型;文献[7]提出的9参数模型等。条带平差方法本质上是通过选择合适的函数模型近似表达各种误差的影响,利用数学变换将原始的激光点坐标纠正到参考坐标系下。由于LiDAR系统误差源众多,许多误差源对定位精度的影响复杂,很难找到一种最优的数学模型,平差精度受模型选择的限制。
系统检校方法则是从激光脉冲的原始观测信息出发(激光脉冲发射时的位置和姿态信息,扫描角度以及激光脉冲测距值等),采用严格的物理模型来描述各项系统误差对于激光点坐标的影响,通过平差直接解算系统误差项,是一种理论上严密的方法。在文献[2,8]中对LiDAR系统误差源以及检校流程进行了阐述,文献[9]中给出了一种分步手工检校方法,文献[10—13]中介绍了几种利用共面条件进行表面匹配的方法。与条带平差方法相比,这类算法以严格物理模型为基础,直接对系统误差源进行补偿,平差精度和稳定性都较好。但这类方法也存在以下缺点:首先,系统误差源众多,许多误差项之间存在强相关性,需要选择合适的误差项进行平差;其次,系统检校需要确定不同条带上的同名特征作为平差约束条件,现有方法大都采用平面作为对应特征,利用共面约束进行平差,需要在测区内提取不同坡向、不同坡度的平面,对测区要求较苛刻,在实际应用中常常难以满足。
本文详细分析了LiDAR系统安置误差对激光点定位精度的影响,介绍一种LiDAR系统安置参数的严格自检校方法,针对离散激光点之间不存在真实同名点的问题,提出一种虚拟连接点模型,解决了激光点之间的同名对应问题。通过两组试验,验证方法的可行性和有效性。
2 安置误差自检校方法
2.1 安置误差的定量分析
机载LiDAR系统通过三角测量方式获取激光点的三维坐标。每个激光点的原始观测信息包括脉冲发射时刻激光器的位置和姿态,扫描镜扫描角度,脉冲观测距离等,按照激光点直接定位的严格模型[14],每个激光点坐标可以有其原始观测信息,按式(1)计算得到(采用局部摄影测量坐标系作为坐标参考)
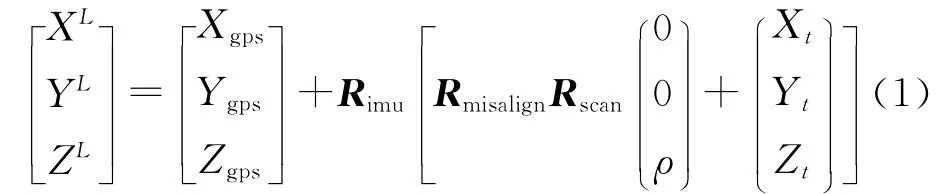
式中,[XL,YL,ZL]T为解算出的激光点三维坐标;[Xgps,Ygps,Zgps]T为GPS天线中心坐标;Rimu为由IMU姿态旋转矩阵;Rmisalign为视准轴偏角旋转矩阵;Rscan为扫描角旋转矩阵;ρ为激光脉冲测距值;[Xt,Yt,Zt]T为系统杆臂偏移。
由公式(1)可知,当IMU姿态角一定时,杆臂偏移对定位精度的影响成简单线性关系,而视准轴偏角对定位精度的影响与扫描角和测距值相关。下面对视准轴偏角的影响进行定量分析。为了简化,假设姿态旋转矩阵为单位矩阵,即X方向为飞行方向,Y方向为扫描方向,三个视准轴偏角分别为roll=0.1°,pitch=0.1°,heading=0.1°。激光点误差在三个坐标轴上随扫描角以及测距值变化见图1、图2、图3。
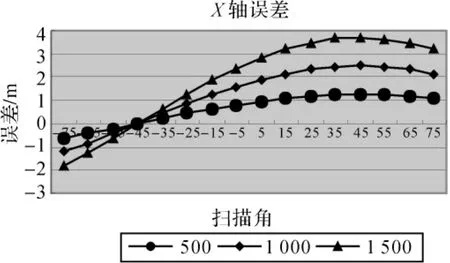
图1 视准轴偏角对X轴定位精度影响Fig.1 X-axis error by boresight misalignment

图2 视准轴偏角对Y轴定位精度影响Fig.2 Y-axis error by boresight misalignment

图3 视准轴偏角对Z轴定位精度影响Fig.3 Z-axis error by boresight misalignment
分析可见,安置误差对于激光点定位精度的影响有以下几个特点:
(1)安置误差对激光点平面和高程精度都有影响。
(2)安置误差中杆臂偏移的影响成线性关系,视准轴误差的影响成非线性关系。
(3)视准轴误差对激光点三个方向影响不同,在飞行方向上当扫描角为-45°时误差最小,随扫描角增大误差增大(图1);在垂直飞行方向上,扫描角0°时误差最大,随扫描角增大误差减小(图2);在高程方向上,扫描角0°时误差最小,随扫描角增大误差增大(图3)。
从三个图中可以发现,测距值会放大视准轴误差,因此航高越高,误差越明显。
2.2 平差模型
将杆臂偏移和视准轴偏角6个安置参数作为未知数,激光点坐标作为观测值,可列出观测方程(2)

未知数X= [Xt,Yt,Zt,ω,φ,κ]T;观测值L=[Xp,Yp,Zp]T,按照间接平差方式可列出误差方程(3)

式中,l=L-(AX0+Δ)=L-L0;A为待求未知数的系数矩阵;L0、X0分别为观测值的近似值和未知数近似值为未知数的改正数。按照最小二乘原理解算得式(4)

式中,P是观测值的权阵,假设观测值都是同精度,P可取为单位矩阵。对于不同形式的观测方程,A和L的具体形式有所不同,本文提出了一种基于虚拟连接点模型的平差方法,平差解算的具体形式将在2.4节中给出。
2.3 虚拟连接点模型
从平差的函数模型可见,每个激光点的三维坐标可以建立三个方程,只需要确定2个以上的激光点,就可按照间接平差原理解算出安置参数的最小二乘解。将不同条带上的同名点坐标均值作为观测值,通过自检校平差使各条带上同名点偏差的平方和最小,并解算出系统安置参数。
由于LiDAR系统离散采样的工作方式,使得在不同的扫描条带上并不存在真实意义上的同名点,这也是通常认为同名点对应方式不适用于LiDAR数据的原因。为了解决离散激光点的对应性问题,提出一种虚拟连接点模型VTPM(virtual tie point model)。如图4,点p和点q为两个激光扫描条带上选取的一对同名点。p、q并不是真实的激光点,将连接点p及其周围三个真实激光点p1、p2、p3组合成一个虚拟连接点P,连接点q及其周围三个真实激光点q1、q2、q3组合成虚拟连接点Q,将点的对应转换为三角形面片对应。由于连接点p位于p1、p2、p3所构成的三角形面片内部,设定两个规则来计算p点坐标。

图4 虚拟点模型Fig.4 Virtual tie point model
规则1:假设三个激光点p1、p2、p3与连接点p共面,按照线性内插方式可计算出p点的高程值。
设p1、p2、p3坐标分别为点的平面坐标为(X,Y),则p点的高程如式(5)
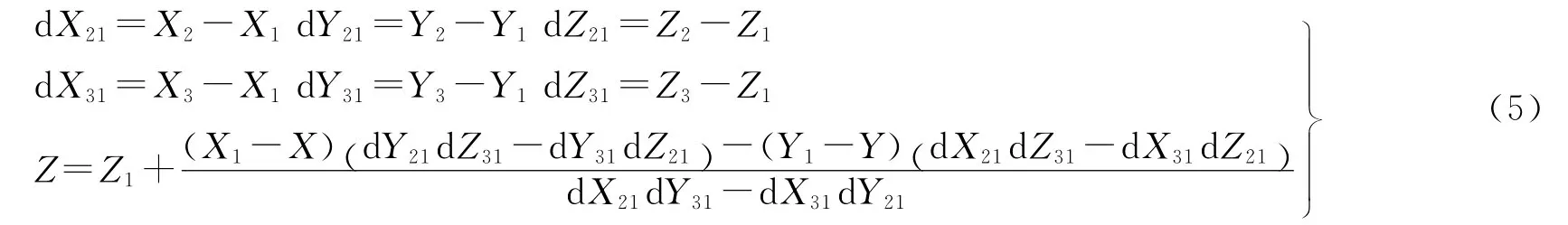
规则2:当LiDAR系统参数发生改变时,激光点坐标也会随之发生变化。
三个激光点距离p很近时,可以认为三个点之间的扫描角和测距变化都很小,将虚拟连接点模型中的微小三角形面片看成是刚体,连接点坐标的改变满足刚体变换,因此可以根据刚体变换参数计算出新的连接点坐标。刚体变换公式如式(6),[X0,Y0,Z0]T是变换前坐标,[X1,Y1,Z1]T是变换后坐标,Rrigid为刚体变换旋转矩阵,[Δx,Δy,Δz ]T为刚体变换的平移量。
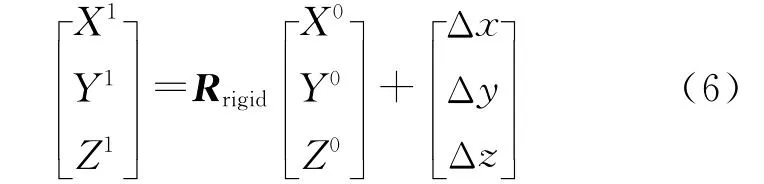
按照以上两个规则,即可将连接点用真实的激光点表示,从而将虚拟的同名点对应转化为真实的激光点对应。
2.4 算法流程
结合安置误差自检校的函数模型以及虚拟点模型,可按图5的流程设计算法。
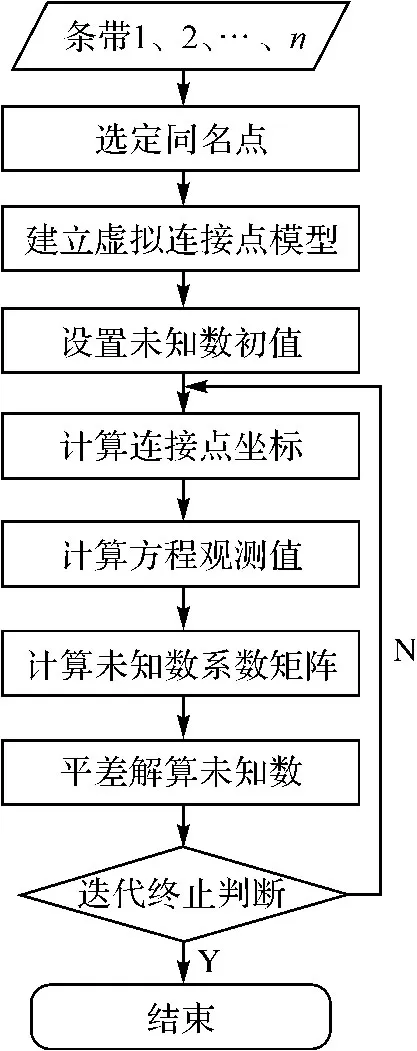
图5 安置误差自检校平差流程Fig.5 Flow chart of mounting error self-calibration
算法中各步骤具体处理过程如下:
(1)选定同名点。采用手工选点方式从不同的激光扫描条带上确定同名连接点,要求所选的同名连接点位于局部平面内,可采用激光高程信息和反射强度信息来辅助选点。激光强度信息反映了不同地物对激光脉冲的反射差异,可用来确定同名点的平面位置。在选取同名点时,可以选择道路斑马线,中心线等激光强度对比明显且局部平坦的区域[15]。
(2)建立虚拟连接点模型。对手工选定的同名连接点按以下方式建立虚拟点模型:首先提取连接点周围指定半径内(如1m,可根据平均点间距确定)的激光点,然后利用RANSAC(random sample consensus)算法[16]从中选出共面点,最后对所有共面点建立Delaunay三角网,选择包围连接点的三角形,并将该三角形的三个顶点作为虚拟点模型中的三个激光点,保证每个虚拟点模型中所选的激光点为手工选定的同名连接点最邻近的三个共面激光点。
(3)设置未知数初值。平差解算未知数是系统安置参数,初次执行时,可根据先验知识设定安置参数的近似值,也可将安置参数都设为0。
(4)计算连接点坐标。利用虚拟点模型计算各条带上的同名连接点坐标。对于同名点k在第i条带上的坐标为[Xki,Yki,Zki]T,在第一次计算时,由于平面坐标(Xki,Yki)在手工选择时已经确定,可按照公式(5)计算Zki;在迭代过程中,按照公式(1)利用当前未知数近似值计算虚拟点模型中三个激光点坐标,用当前激光点坐标和前一次的激光点坐标估算刚体变换参数,并对前一次的连接点坐标按公式(6)进行刚体变换,得到新的连接点坐标。
(5)计算方程观测值。将各条带上同名点坐标的平均值作为坐标观测值,如同名点X坐标计观测值可按式(7)计算。
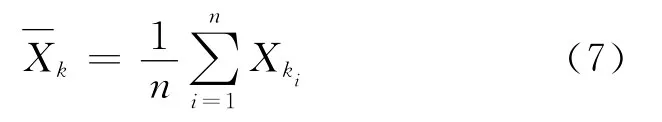
(6)计算未知数系数矩阵。依据2.2节中的平差模型和步骤(5),列出误差方程(8)

对方程进行线性化,得到未知数的系数矩阵为

按步骤(4)计算连接点坐标,[Xki,Yki,Zki]T与作为未知数的安置参数之间存在复杂的非线性关系,直接写出方程线性化后的解析形式非常困难,采用有限差分法计算未知数系数矩阵。例如连接点X坐标表示为式(9),对视准轴偏角ω的偏导数可按公式(10)计算。这里采用的是中心差分,能够保证结果具有二阶精度。利用差分方式计算出未知数的系数矩阵。

对应公式(4),A和l的具体形式为式(11)、式(12)。
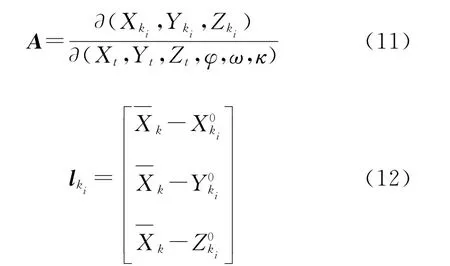
(7)平差解算未知数。在平差解算时,用LM算法进行优化[17],保证法方程秩亏时也能得到收敛的数值解。
(8)迭代终止判断。将残差是否收敛以及未知数是否改变作为迭代终止条件,满足其一则迭代终止,输出安置参数的平差结果;两者都不满足,则将当前结果作为未知数近似值,返回步骤(4)重新执行。
3 试验与分析
3.1 试验描述
试验采用Leica公司生产的ALS50II,该系统采用波长为1 064nm激光进行探测,激光发射频率最大可达150kHz,测距范围200~7 563m,飞行高度200~6 000m,扫描频率0~90Hz,最大扫描角为75°,系统具有记录多次回波能力,最大可记录四次回波数据。试验区域位于河南省安阳市内,地形平坦,建筑物较多,植被比较稀疏。在试验区域采集了8条激光扫描条带,前四个条带呈十字交叉,沿东西向、南北向飞行(图6(a)),同向两条带间具有较大重叠,条带1、条带2飞行高度760m,平均点间距约为0.5m,条带3、条带4飞行高度为1 310m,平均点间距为0.9m;后四个条带沿东西向飞行,相邻条带间重叠约为15%(图6(b)),飞行高度为3 200m,平均点间距为2.1m。

图6 试验区域激光扫描条带Fig.6 LiDAR strips on experimental area
将试验数据分为两组,前四个条带为第一组,用来进行系统检校,后四个条带为第二组,利用检校参数纠正后评价精度。为了验证检校的精度,采用Leica公司提供的Attune[18]软件检校结果与本文方法比较。Attune软件采用的检校算法见文献[10],主要检校LiDAR系统视准轴偏角。在试验1中,采用本文方法对第一组数据进行系统安置误差检校,分析虚拟连接点自检校的可行性和有效性。在试验2中,利用试验1中检校的结果和Attune检校的结果分别对第二组数据进行纠正,对比分析两种方法的检校精度。由于Attune不检校系统杆臂偏移,利用Attune结果进行条带纠正时,将杆臂偏移都设为0。
3.2 结果分析
3.2.1 试验1
在激光扫描强度图像上选取5组同名连接点,进行安置参数自检校试验,连接点分布如图7。选取的同名连接点如图8。

图7 激光条带上的同名点与检查平面Fig.7 Corresponding points and planes on strips

图8 选择的连接点Fig.8 The selection of connection point
将算法迭代过程中连接点坐标与最终连接点坐标比较,图9为5组同名点中的1号点前20次迭代坐标差值变化曲线。可见迭代过程中连接点X、Y、Z坐标都趋向于收敛,而平面坐标收敛较快。可见由虚拟连接点模型计算出的连接点坐标是稳定可靠的。
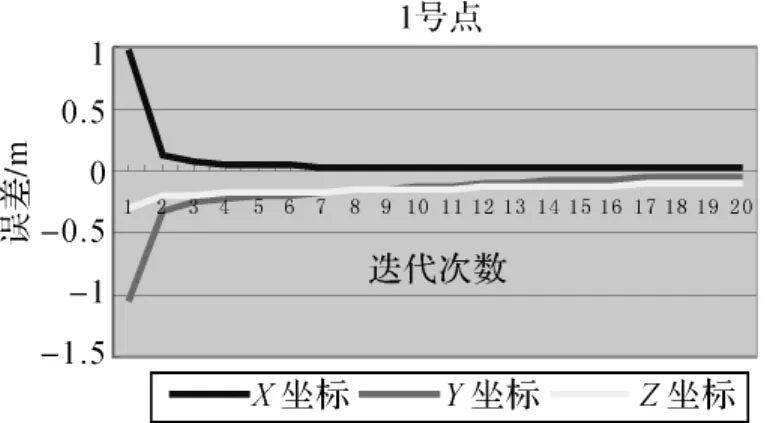
图9 连接点坐标变化规律Fig.9 Trend of coordinate change of connection points
在扫描条带的相同位置选择高程剖面,目视检查平差前后激光点的吻合情况,图10(a)为平差前的高程剖面,人字顶房屋和水平地面都存在较大错位,条带间水平误差更大;图10(b)为平差后的高程剖面,人字顶房屋和水平地面吻合得非常好。用激光强度图像可以直观地检查出个条带间的平面误差,图11(a)为平差前四条扫描条带的强度影像叠加图,平面误差造成机场跑道中心线错位,图11(b)为平差后强度影像叠加图,平面误差已得到很好的纠正。
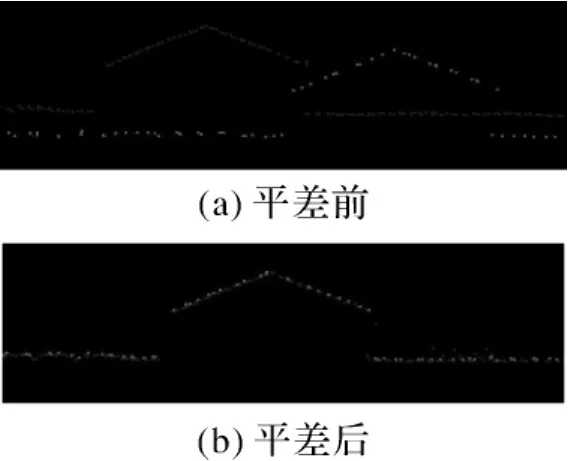
图10 自检校平差前后高程剖面对比Fig.10 Contrast of profile

图11 平差前后各条带强度图像对比Fig.11 Contrast of LiDAR intensity image
定量分析平差结果,计算5组同名点所对应的激光条带上12个连接点坐标平差前后的残差及中误差(表1)。平差后,连接点残差都得到改善,平面残差在0.1m以内,最大为0.179m,考虑到激光点采样间距大于0.5m,选点时存在的插值误差,平差后水平精度优于1/2点间距。高程残差最大为0.07m,说明高程精度明显高于平面精度。

表1 连接点残差平差前后对比Tab.1 Contrast of residual error of connection points m
3.2.2 试验2
利用Attune检校获得的参数与本文方法自检校获得的安置参数分别对后4个激光扫描条带进行纠正,选取高程剖面对纠正前后的激光点相对精度进行目视检查。图12为某个高程剖面上的激光点数据在纠正前后对比。其中,图2(a)为条带纠正前,图2(b)为采用Attune检校得到的视准轴偏角纠正,图2(c)为采用本文检校后得到的安置参数纠正,可见纠正后,条带间的相对精度都得到了提高,两种方法在视觉上差距不大。

图12 安置参数纠正前后高程剖面对比Fig.12 Contrast of profile
为了定量比较两种方法的检校精度,在后4条扫描条带的重叠区内选择7组同名点作检查点,两个平面作为检查平面,对纠正前后的相对精度进行定量分析。第二组数据的激光点间距较大,同名点一般选在道路交叉口,两个检查平面一个选在道路中心区域并避开车辆的影响,另一个选在某运动场中心区域。7组同名点对应的14个连接点的坐标残差在纠正前后对比见表2。采用检校参数纠正后,检查点坐标残差明显减小,利用Attune检校结果纠正后,平面坐标最大残差为1.735m,高程最大残差为0.35m,利用本文方法检校结果纠正后,平面最大残差为1.139m,高程最大残差为0.352m,平面最大残差在约为1/2点间距,Y方向的残差比X方向残差大,这与试验1中的残差分布一致。比较检查点坐标中误差可见,VTPM纠正后的平面精度明显优于Attune,高程精度略低于Attune。

表2 检查点残差纠正前后对比Tab.2 Contrast of residual error of check points m
对两个检查平面,计算点到平面的距离,利用点面距离的中误差评价检校参数的相对精度,计算方法见公式(13)。由于两个检查平面都是水平面,从表3可见,系统检校后,高程精度也得到了较大改善,Attune方法的高程精度略好于VTPM。
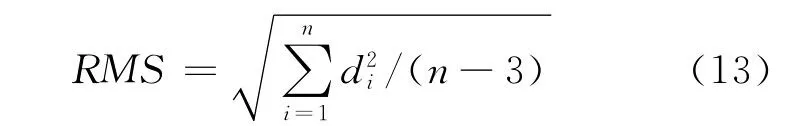
利用检查点和检查平面的中误差对比分析Attune方法和VTPM方法的检校精度,VTPM的平面精度明显优于Attune。这是因为Attune在平差时将激光点到对应平面的距离最小作为平差条件,而VTPM则直接采用对应点之间的距离最小作为平差条件,VTPM能够对三个坐标轴上的偏差直接改正,而Attune需要借助不同坡度的平面来间接改正平面偏差。当检校区域较平坦或选择的连接点不合适时,Attune的平面精度不理想。而Attune在检校时要求选择大量的同名点,这有助于提高检校结果的高程精度,VTPM在试验中仅选择5个虚拟连接点,通过选择更多的虚拟点同样能改善VTPM的高程精度。

表3 检查平面中误差对比Tab.3 RMS error of check planes m
4 结 论
本文所提出的方法可以有效地对LiDAR系统安置误差进行自检校,消除由杆臂偏移以及视准轴偏角所引起的激光扫描条带间平面偏移和高程错位,解算的安置参数稳定有效,可用来对原始激光数据直接进行几何纠正,提高LiDAR数据的相对精度。由于激光扫描离散采样的工作方式,决定了LiDAR数据中没有真实意义的同名点。本文提出了一种虚拟连接点模型VTPM,将虚拟的同名连接点与真实的激光点联系起来,解决了LiDAR数据中的离散点对应问题,实现了基于同名点的系统自检校。VTPM方法与传统的面对应方法相比,对检校场要求较低,只需要在局部平坦的区域内,存在一定辐射差异,能从激光强度影像上确定同名点即可。此外,该方法还能方便引入地面控制点数据进行平差,改善LiDAR数据的绝对精度。通过试验对比VTPM方法与Attune方法,VTPM只需要选取少量连接点就能达到与Attune相似的高程精度,而平面精度更高。
[1] BALTSAVIAS E P.Airborne Laser Scanning:Basic Relations and Formulas[J].ISPRS Journal of Photogrammetry and Remote Sensing,1999,54(2-3):199-214.
[2] MORIN K W.Calibration of Airborne Laser Scanners[D].Calgary:University of Calgary,2002.
[3] HABIB A F,AL-DURGHAM M,KERSTING A P,et al.Error Budget of LiDAR Systems and Quality Control of the Derived Point Cloud[C]∥Proceedings of the ISPRS 2008 Congress.Beijing:ISPRS,2008.
[4] SHAN J,TOTH C K.Topographic Laser Ranging and Scanning:Principles and Processing[M].Boca Raton:CRC Press,2008.
[5] CROMBAGHS M J E,BRÜGELMANN R,DE MIN E.On the Adjustment of Overlapping Strips of Laser Altimeter Height Data[J].International Archives of Photogrammetry and Remote Sensing,2000,33(B3/1):224-231.
[6] KILIAN J,HAALA N,ENGLICH M.Capture and Evaluation of Airborne Laser Scanner Data[J].International Archives of Photogrammetry and Remote Sensing,1996,31:383-388.
[7] VOSSELMAN G,MAAS H G.Adjustment and Filtering of Raw Laser Altimetry Data[C]∥Proceedings OEEPE Workshop on Airborne Laser Scanning and Interferometric SAR for Detailed Digital Elevation Models.[S.l.]:OEEPE Publication,2001.
[8] SCHENK T.Modeling and Analyzing Systematic Errors in Airborne Laser Scanners[R].Columbus:Ohio State University,2001.
[9] ZHANG Xiaohong.Precise Point Positioning Evaluation and Airborne Lidar Calibration[R].Copenhagen:Danish National Space Center,2005.
[10] BURMAN H.Calibration and Orientation of Airborne Image and Laser Scanner Data Using GPS and INS[D].Stockholm:Royal Institute of Technology,2000.
[11] FILIN S,VOSSELMAN G.Adjustment of Airborne Laser Altimetry Strips[J].International Archives of Photogrammetry,Remote Sensing and Spatial Information Sciences,2004,34(B3):285-289.
[12] SKALOUD J,LICHTI D.Rigorous Approach to Boresight Self-calibration in Airborne Laser Scanning[J].ISPRS Journal of Photogrammetry and Remote Sensing,2006,61(1):47-59.
[13] HABIB A F,BANG K I,SHIN S W,et al.LIDAR System Self-calibration Using Planar Patches from Photogrammetric Data[R].Padua:Fifth International Symposium on Mobile Mapping Technology(MMT’07),2007.
[14] VOSSELMAN G,MASS H G.Airborne and Terrestrial Laser Scanning[M].Dunbeath:Whittles Publishing,2010.
[15] TOTH C K,PASKA E,BRZEZINSKA D.Using Road Pavement Markings as Ground Control for Lidar Data[R].Beijing:The International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences,2008.
[16] FISCHLER M A,BOLLES R C.Random Sample Consensus:a Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J].Communications of the ACM,1981,24(6):381-395.
[17] MORÉJ J.The Levenberg-Marquardt Algorithm:Implementation and Theory[M]∥WATSON G A.Numerical Analysis:603.New York:Springer,1978:105-116.
[18] Leica Geosystems GIS &Mapping LLC.ALS Calibration Attune Operation Manual Revision 2[M].Heerbrugg:Leica Geosystems,2003.
Self-calibration of LiDAR System Mounting Biases Using Virtual Tie Point Model
ZHANG Jing,JIANG Wanshou
State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University,Wuhan 430079,China
A self-calibration method for estimating system mounting parameters is introduced.Firstly,using the rigorous model of LiDAR direct geo-referencing,the effect of mounting parameters on laser footprint location accuracy is quantitatively analyzed.Then the self-calibration model based on tie points is given.Laser footprints are discretely sampled,so the real corresponding laser points are hardly existent.A virtual tie point model(VTPM)is proposed to resolve the corresponding problem among discrete laser points.Each VTPM contains a tie point and three real laser footprints.Two rules are defined to calculate tie point coordinate from real laser footprints.The flow of self-calibration based on VTPM is described in detail.The practical examples illustrate the feasibility and effectiveness of the proposed self-calibration method.
LiDAR;self-calibration;mounting biases;lever-arm offset;bore-sight angle;virtual tie point model
ZHANG Jing(1982—),male,PhD candidate,majors in theory and application research of LiDAR.
JANG Wanshou
1001-1595(2011)06-0762-08
P246
A
国家自然科学基金(40671159);国家863计划(2006AA06A208;2007AA120203)
丛树平)
2011-01-26
2011-05-31
张靖(1982—),男,博士生,研究方向为LiDAR数据处理。
E-mail:zhang_jing00@sohu.com
江万寿
E-mail:jws@lmars.whu.edu.cn
