论精密单点定位整周模糊度解算的不同策略

张宝成，欧吉坤

1.中国科学院测量与地球物理研究所 动力大地测量学重点实验室，湖北 武汉430077；2.中国科学院 研究生院，北京100049

论精密单点定位整周模糊度解算的不同策略

张宝成1，2，欧吉坤1

1.中国科学院测量与地球物理研究所 动力大地测量学重点实验室，湖北 武汉430077；2.中国科学院 研究生院，北京100049

由于GPS非差相位观测值的相位偏差（initial phase biases，IPB）与整周模糊度难以分离，精密单点定位（PPP）估值均为模糊度浮点解。首先对GPS原始观测方程的秩亏问题进行分析，从参数整合的角度，推导卫星IPB估计的满秩函数模型，形成一种新的PPP－AR算法。以此为基础，对已有两种算法的特点进行对比分析。研究表明，分解法是一种观测信息的最优利用，且与传统的星钟估计方法具有一致性，但未发掘卫星IPB较为稳定的有利约束；非整法对所采用的组合观测值之间的相关性未加考虑，是一种次优估计，实时性较差，且较依赖于高精度的码观测。推导的新算法可有效克服已有算法的不足，便于施加部分参数的合理时变性约束，提高卫星IPB估计的可靠性。

精密单点定位；初始相位偏差；PPP模糊度固定；分解卫星钟差；非整相位偏差

1 引 言

自1997年Zumberge等人提出PPP概念以来［1］，该技术已广泛地应用于区域或全球坐标框架维持、高精度导航定位、精密授时以及大气延迟提取等领域［2］。与联合多测站GPS观测数据实施网平差相比，PPP在保证解算精度的同时，实施灵活方便且能有效减少计算负担。此外，PPP基于非差GPS观测值，与基于双差观测值的数据处理策略相比，其数据利用率更高，计算结果更为可靠［3］。

PPP目前的发展主要受到两个因素的制约：其一，PPP一般基于IGS等机构发布的卫星轨道和钟差产品，其实时性实施受到一定程度的影响［4］；其二，非差相位观测值中的IPBs与整周模糊度难以分离，使得PPP的各类估值均为模糊度浮点解。若能有效利用非差模糊度的整数特性，PPP的估值精度和收敛特性将有进一步改善的空间［5－12］。

当前，伴随通信技术的发展，基于区域参考站网的GPS观测数据实时估计、播发以及接收卫星轨道和钟差的研究已取得较大进展，在充分考虑数据传输和处理的时延后，实时PPP的定位精度可达到分米甚至厘米级［4］，有效地满足了大部分实时应用的需求。

与此同时，PPP模糊度固定（PPP ambiguity resolution，PPP－AR）的研究已经起步，且形成了两种不同的处理策略：估计分解卫星钟差（分解法）［6，11－14］或非整相位偏差（非整法）［5，7－10］算法。上述两种算法均采用区域或全球范围的GPS网，实时或事后分离卫星IPBs，用于改正PPP相位观测值，还原非差模糊度的整数特性。与标准PPP相比，PPP－AR可有效改善测站坐标解的东分量精度［7，12］。对于远离地面基准站的海上动态平台定位或低轨卫星定轨而言，上述PPP－AR算法还可有效代替目前常用的长基线解算策略［5，9］。

由此可知，为实现PPP－AR，关键在于如何利用GPS网估计卫星IPBs，不同网处理策略构成了现有两种PPP－AR方法的主要差异。此外，第一种方法采用消电离层组合的码、相位观测值以及MW组合观测值，第二种方法对之进一步实施星间单差［6－10，13－14］。上述组合和差分过程“简单”地消除了未知参数个数，但却可能模糊对各类线性相关参数所引起的秩亏现象的认识。

为给出完整的PPP－AR概念，笔者从GPS原始观测方程出发，研究它们的秩亏特性，通过选取适当的基准参数，依次消除了各类秩亏，构建了卫星IPBs估计的满秩函数模型，形成一种PPP－AR新算法。笔者还分别导出了现有两种方法各自的数学模型和理论假设，并从观测数据利用率、实时性以及用户实施等角度进行了对比分析。

2 卫星IPBs估计

本节推导利用参考站网GPS原始观测值估计卫星IPBs的函数模型，针对模型中的秩亏问题，采用参数整合的消秩亏策略。

2.1 秩亏函数模型

忽略观测噪声和多路径等误差，且假定测站和卫星位置已知，则GPS原始观测方程可表示为［15］

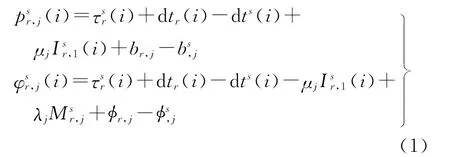
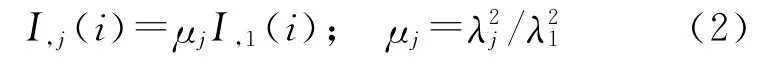
式中，λj表示频率j相位观测值的波长。

假定历元i，n个接收机共观测到m颗共视卫星，以双频观测数据为例，所有线性化方程可联合表示为

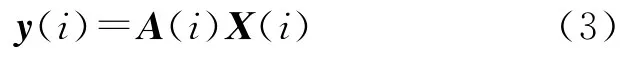
式中

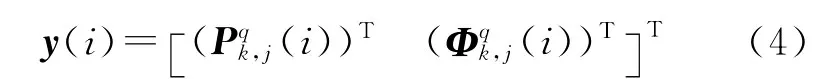
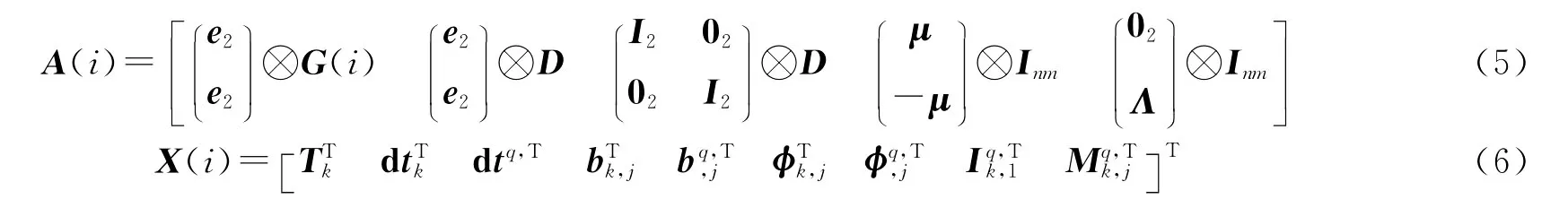
式中，k＝1，…，n、q＝1，…，m和j＝1，2分别代表测站、卫星和频率数；式（4）中的Pqk，j（i）和Φqk，j（i）为所有线性化的码和相位观测值；式（5）中的子矩阵（从左到右）分别对应于式（6）中的各类参数，含义与式（1）相同（省略了历元符号i，以简化表达）。另

式中，⊗、Im和en分别表示克罗内克积［18］、m维单位矩阵以及各元素均为1的n维列向量；Λ为二维对角阵，其对角元为双频GPS观测值的波长

分析A（i）中后四个子矩阵可知，钟差、CIDs、IPBs、模糊度以及电离层延迟之间存在线性相关性，导致A（i）存在列秩亏。

2.2 消秩亏策略

秩亏导致参数估计结果非唯一。为消除该秩亏对参数估计的不利影响，提出如下逐次消秩亏的策略：采用参数整合的方法，将式（6）中的部分参数选取为基准［16］，且遵循如下准则：① 基准参数的个数须与秩亏数相等；②卫星IPBs参数不宜被选取为基准，以确保其独立可估性；③ 最终可估的模糊度须保持其整数特性。具体过程如下：

首先，分析式（8）的D矩阵可知，该矩阵的秩亏源于接收机和卫星的钟差、CIDs以及IPBs之间的线性相关，将某测站（即基准站，此处假定为第一个参考站）的接收机钟差dt1、双频CIDs b1，j和IPBsφ1，j选取为基准。其余测站和卫星的相应参数可表示为

式中，p＝2，…，n。此时，A（i）中对应的第二和第三个子矩阵可表示为

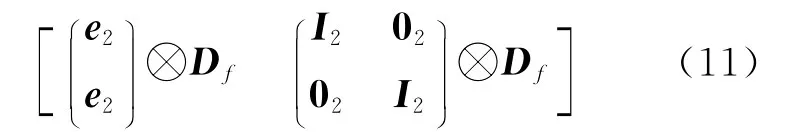
式中

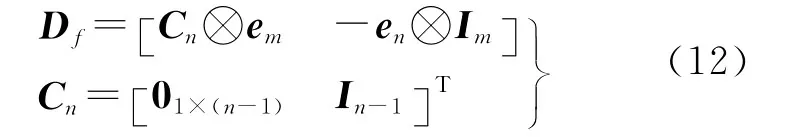
其次，考察式（11）可知，该矩阵的秩亏数为n＋m－1，且源于CIDs与钟差之间的线性相关性。将第一个频率的CIDs（式（10）中的和）选取为基准，可有效消除该秩亏，得到满秩矩阵和待估参数可分别表示为

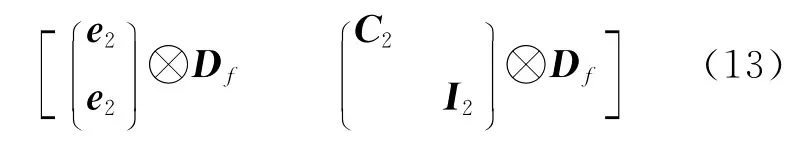
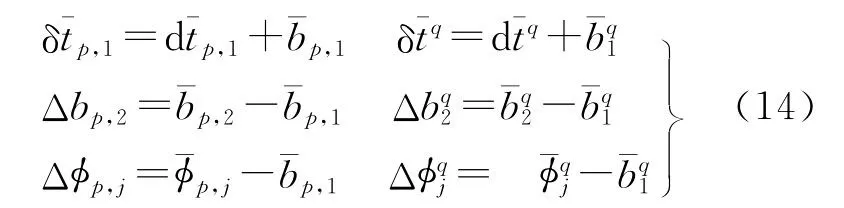
第三，单独考察第j个频率的卫星IPBs和模糊度的设计矩阵

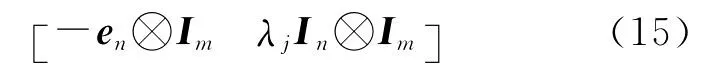
该矩阵秩亏数为m。解决的办法是将基准站观测到的m颗卫星的模糊度Mq1，j作为基准，得到的满秩矩阵和可估参数分别为

由式（17）可知，经由此步消秩亏，非差整周模糊度被参数化为站间单差的形式。随后，考察第j个频率的接收机IPBs和该单差模糊度的设计矩阵

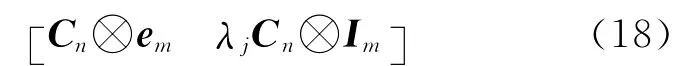
该矩阵秩亏数为n－1。可通过选取某卫星（即基准星，此处假定为第一颗卫星）至所有参考站（除基准站）的单差模糊度作为基准，得到满秩矩阵和可估参数分别为

式中，t＝2，…，s。至此，站间单差的模糊度被参数化为双差的形式，其整数特性可在参数估计过程中加以合理的考虑。

最后，经过上述消秩亏过程后，钟差、CIDs、IPBs以及电离层延迟参数的设计矩阵可联合表示为

式（21）对应矩阵的秩亏数为n＋m－1，可将第二个频率的CIDs（Δbp，2和Δbq2）选取为基准，以消除该秩亏。

至此，通过上述的逐项分析，选取适当的基准参数，经参数整合，原矩阵A（i）中的列秩亏可被充分消除，得到的满秩设计矩阵及部分待估参数分别为

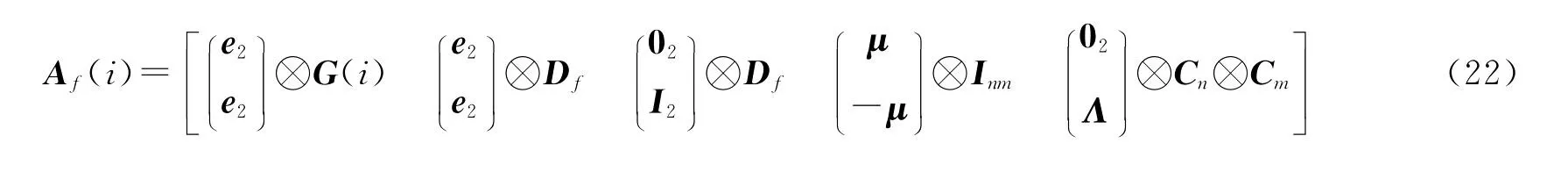
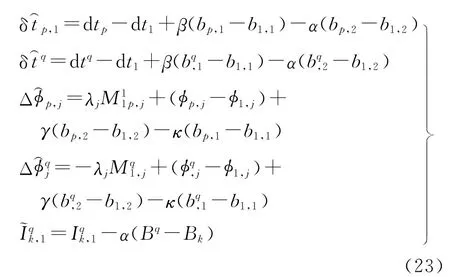
在实际数据处理中，基于上述推导的观测方程，先固定双差模糊度，随后回代，即可求解得到卫星的IPBs和钟差等参数的模糊度固定解，再播发给PPP用户使用。

3 现有PPP－AR策略分析

由上节的满秩函数模型出发，本节推导了两种现有PPP－AR方法的模型，并分别从观测信息利用率、实时性以及用户实施等方面进行了对比分析。

3.1 分解法

分解法［6，11－14］采用消电离层组合的码和相位观测值，在观测域事先消除电离层延迟的影响。通过引入MW组合观测值，将消电离层组合模糊度转换为宽巷和窄巷模糊度，同时有效保留原始观测值中的信息。上述三类组合观测值与原始码、相位观测值之间的转化关系为

事实上，将列满秩的转换矩阵Γ⊗Inm（rk（Γ⊗Inm）＝rk（Γ）rk（Inm）＝cl（Γ⊗Inm）＝3 nm，其中rk（）和cl（）分别表示矩阵的秩和列数［18］）乘以式（22）中的Af（i），且合并双频的IPBs和模糊度参数，可得到式（24）中组合观测值所对应的设计矩阵以及可估参数。具体形式分别为

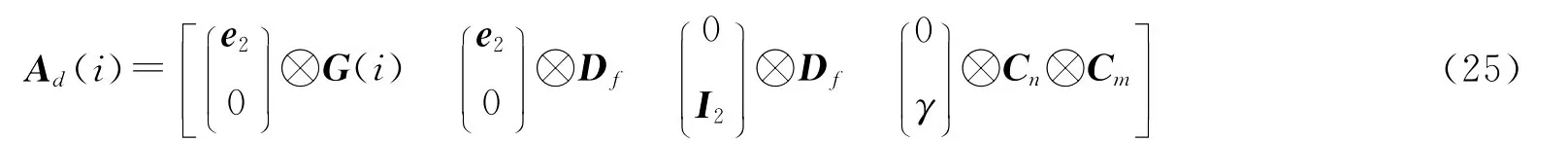
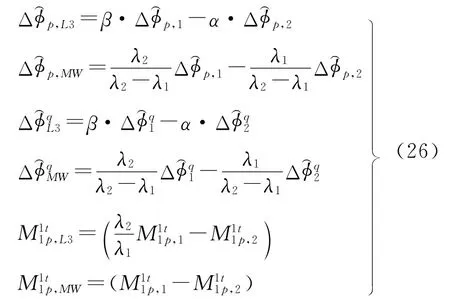
式中，Ad（i）中不再包含电离层延迟的设计矩阵，其余子矩阵与Af（i）中的对应部分含义相同；和分别为中的站星IPBs；和为的站星CIDs；和分别为和的模糊度参数，其波长因子为其余参数的含义同式（23）。站星钟差和天顶对流层延迟等参数的形式未受转换矩阵的影响，此处不再列出。

传统的卫星钟差估计算法中，码和相位观测方程中包含的可估钟差参数形式一致［4］，该参数化形式可导致钟差估值易受码观测值的影响，进而出现日间不连续等异常现象［19］。在分解法的参数估计过程中，码和相位分别对应不同类型的钟差参数，具体为将式（26）中的和与对应于的站星钟差合并，且模型化为具有白噪声特性的时变参数，由此得到对应于的新站星钟差分别为

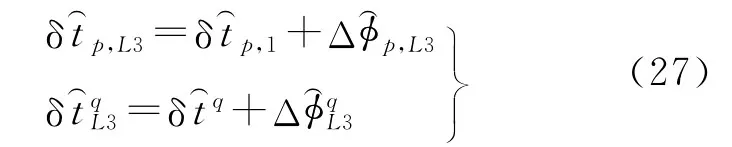
至此，分解法函数模型的设计矩阵可表示为

基于上述推导得到的函数模型，分解法的实施特点可概括如下。

该算法基于上述三类组合观测值（式（24））实施参数估计，在有效消除电离层延迟的同时，充分利用了原始观测值中的有效信息。在观测值加权策略中，若合理考虑由于观测值组合所引起的数学相关性，则各类参数估计结果与基于原始观测值等价。

基于卡尔曼滤波算法，分解法可实现各类参数的实时递归估计，模糊度参数的整数特性可在参数估计过程中被合理利用，以有效提高其余各类参数的精度和可靠性。

对于用户而言，PPP－AR的实施与标准PPP类似，区别仅在于消电离层组合的码、相观测值需采用分解法计算得到的分别改正（标准PPP算法中，码、相观测值均采用改正），同时用户可选择MW组合观测值并施加改正以辅助整周模糊度的快速固定。这意味着目前常用的标准PPP软件，经过简单的升级即可满足模糊度固定的要求，故实施过程将比较经济、有效。

3.2 非整法

非整法［5，7－10］基于星间单差的和三类观测值。将差分矩阵I3n⊗［－em－1Im－1］乘以式（29），可得非整法函数模型的设计矩阵

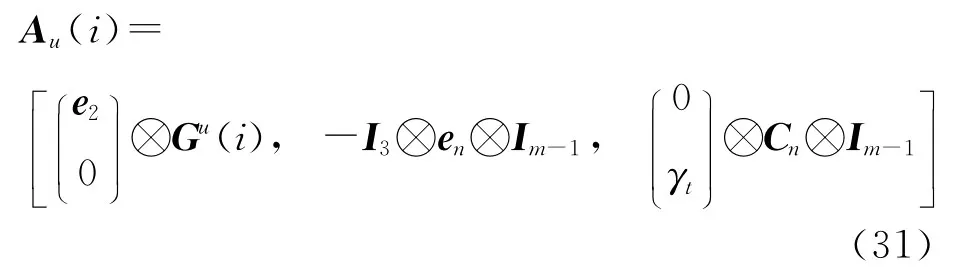
式中

非整法的实施基于如下的分步数据处理策略。

类似于第一步，将连续弧段内的式（34）经由取平均和取整运算，分离得到（窄巷IPBs）的小数部分至此，可将得到的连同播发给PPP用户以实现模糊度解算。

与分解法相比，非整法的实施特点可简要概括如下。

非整法对分解法中所采用的三类组合观测值进一步实施星间差分运算，以消除与测站有关的偏差影响，进而减少了待估参数的个数。然而，由此所引起的各类观测值之间的数学相关性在非整法的分步实施过程中未合理考虑：如计算或均基于逐卫星求解的方法，各卫星单差观测值之间的相关性一般被忽略，导致上述两类估值的精度评定复杂。

此外，非整法取平均过程使得实时参数估计难以实施，不仅如此，简单的取平均运算并不能有效消除部分非模型化误差的影响（如码观测值的多路径等），尤其是当连续弧段的时长较短时，对于较为依赖码观测值的求解过程而言，估值结果往往并不可靠。

最后，由于非整法提供给PPP用户的产品均为星间单差的形式，故用户需要采用相同的星间单差观测值，这与目前标准PPP算法中基于非差观测值的数据处理策略差别较大，用户的软件升级所需成本等代价较之分解法更高。

4 结论与建议

本文推导了利用参考站网GPS原始观测值估计卫星IPBs的满秩观测方程。通过卡尔曼滤波，可估计得到卫星IPBs，为PPP－AR提供一种新算法。作为对比，分别导出了目前常用的两种PPP－AR策略：分解法和非整法的数学模型，并对两种方法的实施特点进行了对比性的论述。分析表明，分解法的参数估计过程充分利用了观测值中的有效信息，便于用户实时或事后实施PPP模糊度解算；非整法采用逐卫星取平均的策略估计星间单差的IPBs，其实时性的实施较为困难，且用户需采用相同的星间单差运算，增加了可能的计算负担。

上述两类方法的本质区别还在于站星IPBs的时变模型选择：分解法认为两类参数随时间变化的特性在参数估计过程中难以有效描述，故该方法将上述两类偏差的消电离层组合项与对应的站星钟差合并，且模型化为具有白噪声性质的参数；与之相反，非整法则认为两类参数均随时间缓慢变化，且其随时间变化的部分可通过简单的取平均加以消除。

与上述两种基于组合或差分观测值的算法不同，本文基于原始观测值估计卫星IPBs的算法具有如下的优势：观测值的组合或差分所引起的数学相关性对于观测值合理定权的不利影响可以较好地避免；可估电离层延迟的平稳时间变化可作为一种有效的约束以增强各类估值的精度与可靠性；站星IPBs的时变性可采用较为合理的模型加以描述（如随机游走），以避免分解法中将其模型化为白噪声所引起的待估参数增多，估值精度不高，同时也可避免非整法中将之过强地约束为时不变参数所引起的可靠性降低等问题。

［1］ ZUMBERGE J，HEFLIN M，JEFFERSON D，et al.Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks［J］.Journal of Geophysical Research，1997，102（B3）：5005－5017.

［2］ ZHANG Baocheng，OU Jikun，YUAN Yunbin，et al.Precise Point Positioning Algorithm Based on Original Dualfrequency GPS Code and Carrier－phase Observations and Its Application［J］.Acta Geodaetica et Cartographica Sinica，2010，39（5）：478－483.（张宝成，欧吉坤，袁运斌，等.基于GPS双频原始观测值的精密单点定位算法及应用［J］.测绘学报，2010，39（5）：478－483.）

［3］ BLEWITT G.Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000km［J］.Journal of Geophysical Research，1989，94（B8）：10187－10203.

［4］ ZHANG Xiaohong，Li Xinxin，Guo Fei，et al.Servicebased Real－time Precise Point Positioning and Its Application［J］.Chinese Journal of Geophysics，2010，53（6）：1308－1314.（张小红，李星星，郭斐，等.基于服务系统的实时精密单点定位技术及应用研究［J］.地球物理学报，2010，53（6）：1308－1314.）

［5］ BERTIGER W，DESAI S D，HAINES B，et al.Single Receiver Phase Ambiguity Resolution with GPS Data［J］.Journal of Geodesy，2010，84（5）：327－337.

［6］ COLLINS P，BISNATH S，LAHAYE F，et al.Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing［J］.Navigation，2010，57（2）：123－135.

［7］ GE M，GENDT G，ROTHACHER M，et al.Resolution of GPS Carrier－phase Ambiguities in Precise Point Positioning（PPP）with Daily Observations［J］.Journal of Geodesy， 2008，82（7）：389－399.

［8］ GENG J，TEFERLE F N，SHI C，et al.Ambiguity Resolution in Precise Point Positioning with Hourly Data［J］.GPS Solutions，2009，13（4）：263－270.

［9］ GENG J，TEFERLE F N，MENG X，et al.Kinematic Precise Point Positioning at Remote Marine Platforms［J］.GPS Solutions，2009，14（4）：343－350.

［10］ GENG J，MENG X，DODSON A H，et al.Integer Ambiguity Resolution in Precise Point Positioning：Method Comparison［J］.Journal of Geodesy，2010，84（9）：569－581.

［11］ LAURICHESSE D，MERCIER F，BERTHIAS JP，et al.Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination［J］.Navigation，2009，56（2）：135－149.

［12］ ZHANG Xiaohong，LI Xinxin.A New Method for Zerodifferenced Ambiguity Resolution and Its Application to PPP［J］.Geomatics and Information Science of Wuhan University，2010，35（6）：657－660.（张小红，李星星.非差模糊度固定解PPP新方法及实验［J］.武汉大学学报：信息科学版，2010，35（6）：657－660.）

［13］ COLLINS P.Isolating and Estimating Undifferenced GPS Integer Ambiguities［C］∥Proceedings of ION National Technical Meeting.San Diego：［s.n.］，2008：720－732.

［14］ COLLINS J P.US 2010／0188285A1Decoupled Clock Model with Ambiguity Datum Fixing［P］.Ottawa：Minister of Natural Resources，2010.

［15］ TEUNISSEN P J G，KLEUBERG A.GPS for Geodesy［M］.2nd ed.Berlin：Springer，1998.188－194.

［16］ OU Jikun.Uniform Expression of Solutions of Ill－posed Problems in Surveying Adjustment and the Fitting Method by Selection of the Parameter Weights［J］.Acta Geodaetica et Cartographica Sinica，2004，33（4）：283－288.（欧吉坤.测量平差中不适定问题解的统一表达与选权拟合法［J］.测绘学报，2004，33（4）：283－288.）

［17］ SCHAFRIN B，GRAFAREND E.Generating Classes of Equivalent Linear Models by Nuisance Parameter Elimination，Applications to GPS Observations［J］.Manuscripta Geodetica，1986，11（3）：262－271.

［18］ AMIRI－SIMKOOEI A R.Least－square Variance Component Estimation：Theory and GPS Applications［D］.Delft：Delft University of Technology，2007.

［19］ LAHAYE F，COLLINS P，CERRETTO G，et al.Advances in Time and Frequency Transfer from Dual－frequency GPS Pseudorange and Carrier－phase Observations［C］∥Proceedings of 40th Annual Precise Time and Time Interval（PTTI）Meeting.Virginia：［s.n.］，2008：415－432.

On the Different Strategies for Integer Ambiguity Resolution in Precise Point Positioning

ZHANG Baocheng1，2，OU Jikun1
1.Key Laboratory of Dynamic Geodesy，Institute of Geodesy and Geophysics，Chinese Academy of Sciences，Wuhan 430077，China；2.Graduate University of Chinese Academy of Sciences，Beijing100049，China

Due to the inseparability between the initial phase biases（IPB）and the integer ambiguities in undifferenced（UD）GPS carrier phase observable，the solutions from precise point positioning（PPP）are always ambiguity－float.The rank－defect UD GPS observation equation is firstly investigated，and the full－rank mathematical model for satellite IPB estimation is derived by means of re－parameterization，thus forming a new strategy for PPPAR.Comparative analysis of the characteristics of both existing methods is subsequently conducted based on the derived re－parameterized equations.It is concluded from the analysis that full utilization of information from GPS observations is guaranteed in DSC method.The process of generating DSC is consistent with the standard satellite clocks estimation.However，the stable temporal behaviors of satellite IPB are not reasonably exploited.In contrast，the FPB method doesn’t fully account for the mathematical correlations between the adopted linear combinations of GPS observations，which would result in a sub－optimal satellite IPB.Additionally，the real－time implementation of this method is more troublesome than the DSC，and the GPS code observations with high accuracy are always required.The newly presented strategy here can avoid the shortcomings in both current methods，and reasonable constraints that are converted from the temporal stability of several unknowns can be easily imposed upon the parameter estimation to lead to more reliable satellite IPB.

precise point positioning（PPP）；initial phase biases（IPB）；PPP ambiguity resolution（PPP－AR）；decoupled satellite clocks（DSC）；fractional phase biases（FPB）

ZHANG Baocheng（1985—），male，PhD candidate，majors in study of applications of precise point positioning and network－based RTK.

1001－1595（2011）06－0710－07

P228

A

国家自然科学基金（40874009；41074013）；国家杰出青年科学基金（40625013）；中国科学院研究生科技创新与社会实践资助专项

丛树平）

2010－10－11

2011－05－16

张宝成（1985—），男，博士生，研究方向为精密单点定位与网络RTK技术的应用。

E－mail：b.zhang＠whigg.ac.cn