中国余数定理在双基线InSAR相位解缠中的应用

张红敏，靳国旺，2，徐 青，秦志远，孙 伟

1.信息工程大学测绘学院，河南 郑州450052；2.中国科学院 电子学研究所 微波成像技术国家级重点实验室，北京100190

中国余数定理在双基线InSAR相位解缠中的应用

张红敏1，靳国旺1，2，徐 青1，秦志远1，孙 伟1

1.信息工程大学测绘学院，河南 郑州450052；2.中国科学院 电子学研究所 微波成像技术国家级重点实验室，北京100190

介绍利用中国余数定理求解同余方程组的基本公式，并将中国余数定理引入到双基线InSAR相位解缠中。构造关于干涉相位模糊数的同余方程组，设计基于中国余数定理的双基线InSAR相位解缠方法，扩展相位解缠的非模糊区间，为解决干涉相位欠采样区域的相位解缠难题奠定基础。利用不同地区的多套DEM仿真的双基线InSAR干涉图进行相位解缠试验，验证该方法在干涉相位欠采样等区域的解缠能力。

中国余数定理；合成孔径雷达干涉测量；多基线；双基线；相位解缠

1 引 言

中国余数定理（CRT，Chinese remainder theory）可用于解决理想两两互素情况下线性同余方程组解的计算问题［1］。该定理在信号处理、密码系统等领域已得到实际应用。文献［2］将中国余数定理应用于多基线相位干涉仪的相位差解模糊；文献［3］研究了基于中国余数定理的同步图像压缩与加密方法；文献［4—5］应用中国余数定理解决SAR动目标成像时的相位模糊问题；文献［6］设计了基于中国余数定理作为陷门的公钥密码系统；文献［7］分析了中国余数定理用于分布式星载SAR－ATI系统解速度模糊的方法。

多基线InSAR技术［8－9］具有高可靠性与高精度优势，已经成为InSAR技术的重要发展方向之一。多基线InSAR获取高精度DEM技术的核心问题之一是相位解缠。考虑到多基线InSAR相位解缠与同余问题的相通性，为了解决多基线InSAR相位解缠难题，笔者从最简单的双基线InSAR基本原理入手，将中国余数定理应用于双基线InSAR相位解缠中。构造了关于干涉相位模糊数的同余方程组，设计了基于中国余数定理的双基线InSAR相位解缠方案。利用多套不同地区DEM仿真的双基线InSAR干涉图进行了相位解缠试验，得到了满意的解缠结果，验证了所设计解缠方案的有效性。

2 中国余数定理

中国余数定理又称中国剩余定理、孙子定理，最早见诸南北朝时期的数学名著《孙子算经》［11］，用于解决理想两两互素情况下线性同余方程组求解问题。

《孙子算经》中记载的“物不知其数”［1］问题是中国余数定理的典型应用：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”用同余式表示“物不知其数”问题，就转化为如式（1）所示的线性同余方程组求解问题。

式中，x为同余方程组的解，x≡a（mod m）表示x和a模m同余，整数m称为同余的模。

《孙子算经》中给出了“物不知其数”问题的解法，程大位进一步在《算法统宗》中给出了计算口诀［11］：“三人同行七十稀，五树梅花廿一枝，七子团圆正月半，除百零五便得知。”数学语言表述，即

式中，a1、a2、a3为余数，满足式（1）的最小正整数解为23。

“物不知其数”问题描述了同余问题的一个典型特例，其解法口诀实际上是中国余数定理的一个特定用法。中国余数定理的表述有多种，依据本文需要，表述如下［1，12］

若m1，m2，…，mn两两互素，a1，a2，…，an是任意整数，则同余方程组

在0≤x＜m＝m1m2…mn内有唯一的解，并且解一定可以写为

式中

3 双基线InSAR获取DEM基本原理

如图1所示，假定主天线相位中心S1和从天线相位中心S2、S3位于同一直线上，三天线相位中心分别形成两副稳定基线，构成单发三收式双基线InSAR系统。记S1的高程为H，S1和S2形成的基线为B，基线水平角为α。沿视线向的基线分量，即平行基线为B‖，垂直于视线向的基线分量，即垂直基线为B⊥。对目标点P的侧视角为θ，干涉图中相邻像元对应的地面点为P′，P′对P的相对高程为dZ，P到天线相位中心S1和S2的斜距分别为R和R－ΔR，ΔR为斜距差。

图1 双基线InSAR几何模型Fig.1 Geometry of dual－baseline InSAR

由图1所示几何关系可知，地面点P的高程Z为

式中，侧视角θ与基线水平角α及角β的关系为

斜距R的计算公式为

式中，R0为SAR系统近距延迟，Mslant为SAR图像斜距向像元大小，y为地面点P对应像点的斜距向坐标。

在△S1S2P中，根据余弦定理有

则

由式（6）、式（7）和式（10），得

记λ为雷达波波长。对于单发多收模式，斜距差ΔR与真实干涉相位Φa的关系为

由于干涉图中记录的是干涉相位主值φ，其值域为［0，2π），在InSAR处理中需要经过相位解缠和干涉相位偏置参数定标才能由φ得到Φa。

式（11）对ΔR求偏导，可得

ΔR相对于R是一个可以忽略的小量，上式可近似为

联立式（12）和式（14），得

整理上式，可得

式中，

Z＊表示引起一个2π干涉相位变化所对应的高程变化，称为高程模糊数。由式（17）不难看出，高程模糊数与垂直基线成反比，垂直基线越长，高程模糊数越小，高程反演精度越高；反之，垂直基线越短，高程模糊数越大，高程反演精度越低。对于如图1所示的几何构型，垂直基线之比等于基线长度之比。为简化算法，本文以基线长度之比代替垂直基线之比。

4 双基线InSAR相位解缠原理

为了将中国余数定理应用于双基线InSAR相位解缠中，需要建立同余方程组形式的双基线InSAR相位解缠模型。

假设在基线分别为B1和B2的情况下获取的缠绕干涉相位分别为φ1和φ2，对应的真实干涉相位分别为Φa1和Φa2，解缠后的干涉相位分别为Φ1和Φ2。根据式（15）可知，同一相对高程dZ与各干涉相位微分dφi（i＝1，2）之间的关系为

式中，ki为dφi的模糊数。

任意有限位数的实数均可以乘以10q（其中，q为该实数的小数位数），保留全部有效位数，转换为无精度损失的整数。因此，可假定基线长度B1、B2均为正整数。两基线长度的最小公倍数为B0＝［B1，B2］，记模mi（i＝1，2）为mi＝B0／Bi。则由式（18）可得

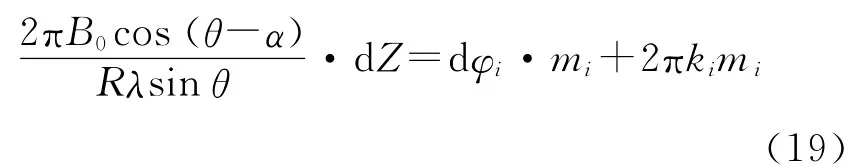
其中，ai取整数，且－mi＜ai＜mi。需要指出的是，余数a1、a2是实际干涉图中缠绕干涉相位微分的函数，是一组实数。并且由于实际中相位噪声的存在，式（20）可能并不成立。然而，在一定的噪声水平下，通过余数取整，仍可将双基线InSAR相位解缠问题视为整数域内的同余问题，表示成线性同余方程组为

因为mi＝B0／Bi，以此方式构造的模m1、m2互素，从而满足了中国余数定理的要求。根据中国余数定理，同余方程组（21）在0≤x＜m内有唯一解，并且解可以写成

式中

式中，M－1i是Mi的乘法逆元，即

求解M－1i是应用中国余数定理的关键之一，可利用扩展欧几里得算法［12］递归求解M－1i。

由中国余数定理求得式（21）在［0，m）的最小正整数解xmin后，可由下式计算两幅干涉图中对应像元处的模糊数ki（i＝1，2），为

式中，余数ai需进行取整，也可写作Int（ai）。那么，两幅干涉图中该像元处解缠后的干涉相位微分dΦi分别为

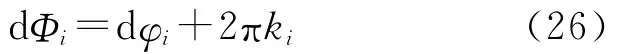
在两幅干涉图中，均以像素（x0，y0）为相位解缠种子，分别对dΦi沿某一路径积分，就可以同时解缠两幅干涉图，即

式中，（x，y）为干涉图像点的方位向和斜距向坐标。

由上述分析可知，将双基线InSAR相位解缠问题转化为线性同余方程组求解问题，突破了传统相位解缠方法对相邻干涉相位差不超过半周期的限制，扩展了正确解缠的非模糊区间，即将非模糊区间从［－π，π）扩展到［－mπ，mπ），从而可以解决干涉相位欠采样和频谱混叠区域的相位解缠难题。

5 双基线InSAR相位解缠流程

基于中国余数定理的双基线InSAR相位解缠包括依据基线情况构造互素模、建立关于缠绕相位微分模糊数的同余方程组、利用中国余数定理求解同余方程组、计算模糊数、求得解缠后的相位微分值、相位积分等关键步骤。其基本流程如图2所示。

图2 基于CRT的双基线InSAR相位解缠流程Fig.2 Phase unwrapping flowchart based on CRT for dual－baseline InSAR

（1）根据配准结果，获取分别对应于基线B1、B2的双基线InSAR干涉图（即缠绕干涉相位）φ1、φ2。构造互素模m1、m2

式中，B0＝［B1，B2］。当B1、B2为有限位数的小数时，首先将其同时扩大整数倍，转化为正整数。

（2）计算相邻像素（x1，y1）和（x2，y2）之间的缠绕干涉相位微分dφ1、dφ2

（3）构造a1、a2。由dφ1、dφ2构造同余方程组的余数a1、a2，并进行取整，将同余方程组纳入整数环

（4）建立线性同余方程组。建立关于缠绕相位微分的模糊数k1、k2的同余方程组

（5）计算p。根据中国余数定理，在0≤p＜m1m2内，解同余方程组，得到p。其中，乘法逆元利用扩展欧几里得算法迭代求解。

（6）计算k1、k2。模糊数k1、k2为

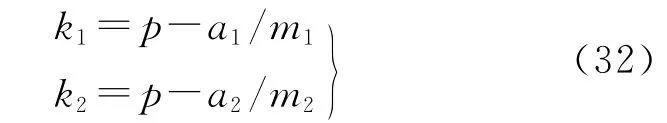
（7）计算dΦ1、dΦ2。解缠后的干涉相位微分dΦ1、dΦ2为

（8）进行相位积分，计算干涉图任意像元的解缠干涉相位Φ1、Φ2。分别以给定的相位解缠种子φ1（x0，y0）、φ2（x0，y0），对dΦ1、dΦ2沿某一路径积分，得到两幅干涉图的解缠结果

6 试 验

为了验证基于中国余数定理的双基线InSAR相位解缠方法的有效性，本文利用不同地区的DEM仿真了多套双基线InSAR干涉图，进行了相位解缠试验。采用的DEM如图3所示，其中（a）为由SIR－C／X－SAR干涉数据获取的天山地区10m格网间距的DEM，（b）为SRTM获取的海南地区90m格网间距的DEM。为了充分验证该方法对含任意有限位小数基线情况的适用性，试验中，选择的基线长度既有整数也有一般实数。所用仿真参数如表1所示，仿真的去平地效应后的双基线干涉图如图4所示。

图3 DEMFig.3 DEM

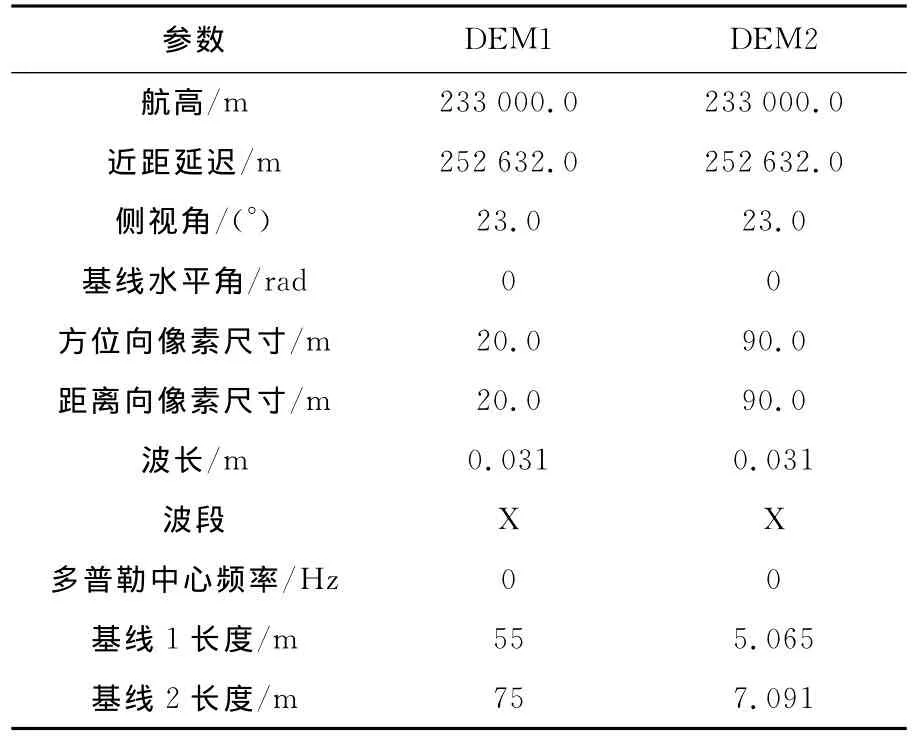
表1 干涉图仿真参数Tab.1 Parameters of interferogram simulation

图4 仿真的双基线干涉图Fig.4 Simulated dual－baseline InSAR interferograms

由图3和图4不难看出，天山及海南地区的仿真干涉图中均存在欠采样和频谱混叠现象。为了突出单基线InSAR技术在欠采样和频谱混叠区域的相位解缠问题，在进行相位解缠时，两类解缠方法均采用沿距离向直接相位积分策略。其中，单基线解缠结果如图5所示；基于中国余数定理的双基线相位解缠结果如图6所示。

图5 单基线相位解缠结果Fig.5 Unwrapped interferograms with single baseline

图6 基于中国余数定理的双基线相位解缠结果Fig.6 Unwrapped interferograms with dualbaseline based on CRT

由图5不难看出，由于仿真干涉图中存在频谱混叠现象，采用单基线相位解缠方法，难以得到良好的相位解缠结果。并且，由于积分路径没有绕开残差点，误差传递导致了整行解缠错误的点，从而更加鲜明地反映了单基线InSAR技术在频谱混叠区域的相位解缠困境。采用基于中国余数定理的双基线InSAR相位解缠方法时仍采用相同的积分路径，由图6易知，天山和海南地区的仿真双基线干涉图均得到了良好的解缠效果，解缠后的干涉图所显示的地形起伏状况分别与图3 DEM1和DEM2所显示的地形相吻合，较长基线对应的解缠后干涉图包含更多的细部信息。为直观比较两种方法的解缠差异，分别计算了两种方法对天山地区仿真干涉图的解缠结果（图5（a）（b）和图6（a）（b））与理论结果的较差图，分别如图7和图8所示。

对比图7和图8可知，基于中国余数定理的相位解缠方法通过将双基线相位解缠问题转化为线性同余方程组的求解问题，扩展了正确解缠的非模糊区间，从而解决了频谱混叠区域的相位解缠难题。以海南地区仿真干涉图的相位解缠为例，采用单基线InSAR相位解缠方法时，正确解缠的非模糊区间为［－π，π）；而采用本文所设计的双基线InSAR相位解缠方法时，正确解缠的非模糊区间扩展为［－mπ，mπ），从而能够正确解缠频谱混叠区域的缠绕相位。其中，m＝35，计算过程如下：

图7 单基线相位解缠结果与理论解缠结果较差图Fig.7 Interferogram difference between unwrapped interferograms with single－baseline and unwrapped interferograms in theory

图8 双基线相位解缠结果与理论解缠结果较差图Fig.8 Interferogram difference between unwrapped interferograms with dual－baseline and unwrapped interferograms in theory

记基线B1和B2扩大取整后对应值分别为B′1和B′2

B′1和B′2的最小公倍数B′为

构造模m1和m2分别为

m是模m1和m2的最小公倍数，为

由图8易知，在无噪声情况下，采用所设计方法，不同地区仿真干涉图均得到了良好的解缠结果，验证了所设计方法的正确性和有效性。

为了分析噪声对基于中国余数定理的双基线InSAR相位解缠方法的影响，又采用仿真含噪声干涉图进行了试验。在利用天山地区DEM仿真干涉图时，加入了均值为0，方差为0.000 2rad2的随机相位噪声，干涉图仿真结果如图9所示。

图9 仿真的含噪声双基线干涉图Fig.9 Simulated dual－baseline interferograms with noise

对图9所示含噪声干涉图，采用直接相位积分的单基线InSAR相位解缠方法进行相位解缠的结果如图10所示；采用基于中国余数的双基线InSAR相位解缠方法进行相位解缠，结果如图11所示。

由图10和图11可以看出，两种方法的解缠结果均受到了噪声的影响，出现了解缠错误的点并导致了沿积分路径的误差积累。其中，基于中国余数定理的解缠结果中部分解缠错误区域如图11中方框所示。为了避免噪声影响引起的误差积累，下一步研究中将选择避开残差点的积分路径进行基于中国余数定理的双基线InSAR相位解缠。关于噪声量值对本文算法的定量影响及其解决方案将在后续工作中进行深入研究。

图10 单基线相位解缠结果Fig.10 Unwrapped interferograms with single baseline

图11 基于中国余数定理的双基线相位解缠结果Fig.11 Unwrapped interferograms with dualbaseline based on CRT

7 总 结

中国余数定理是解决同余问题的有效方法，而多基线InSAR相位解缠的实质可认为是同余问题。为了给多基线InSAR相位解缠提供良好技术方案，本文着眼于最简单的双基线InSAR技术，将中国余数定理应用于双基线InSAR相位解缠中，设计了基于中国余数定理的双基线InSAR相位解缠方法。采用SIR－C／X－SAR获取的天山地区DEM和SRTM海南地区DEM仿真的双基线InSAR干涉图，进行了相位解缠试验，得到了理想的解缠结果。通过进一步对仿真含噪声干涉图的解缠试验，验证了一定噪声水平下，该方案的正确性和有效性。与单基线相位解缠结果对比，验证了多基线InSAR技术高可解缠性的优势。

论文成果为进一步研究三基线以上的InSAR相位解缠方案提供了参考。在后续研究中，将把该方法扩展至三基线以上的相位解缠中；研究基线组合方案对相位解缠的影响；研究噪声对相位解缠的影响，及采用质量图区域生长、选择避开残差点的积分路径以及利用优化思想改化同余方程组等方法，减弱噪声对解缠结果的影响。

［1］ PEI Dingyi，ZHU Yuefei.Algorithmic Number Theory［M］.Beijing：Science Press，2002.（裴定一，祝跃飞.算法数论［M］.北京：科学出版社，2002.）

［2］ ZHOU Yaqiang，CHEN Zhu，HUANG Pukan，et al.Algorithm of Solving Multi－baseline Interferometer Phase Difference Ambiguity in Noisy Circumstance［J］.Journal of Electronics and Information Technology，2005，27（2）：259－261.（周亚强，陈翥，皇甫堪，孙仲康.噪扰条件下多基线相位干涉仪解模糊算法［J］.电子与信息学报，2005，27（2）：259－261.）

［3］ JAGANNATHAN V，MAHADEVAN A，HARIHARAN R，et al.Number Theory Based Image Compression Encryption and Application to Image Multiplexing［C］∥Proceedings of International Conference on Signal Processing，Communications and Networking.Chennai：［s.n.］，2007：59－64.

［4］ XIA Xianggen，WANG Genyuan.Phase Unwrapping and a Robust Chinese Remainder Theorem［J］.IEEE Signal Processing Letters，2007，14（4）：247－250.

［5］ LI Xiaowei，XIA Xianggen.A Fast Robust Chinese Remainder Theorem Based Phase Unwrapping Algorithm［J］.IEEE Signal Processing Letters，2008，15：665－668.

［6］ YASUYUKI M，KIYOKO K，MASAO K.A New Class of Cryptosystems Based on Chinese Remainder Theorem［C］∥Proceedings of International Symposium on Information Theorem and Its Applications.Auckland：［s.n.］，2008：1－6.

［7］ QI Weikong，DANG Yawen，YU Weidong.Deblurring Velocity Ambiguity of Distributed Space－borne SAR Based on Chinese Remainder Theorem［J］.Journal of Electronics and Information Technology，2009，31（10）：2493－2497.（齐维孔，党雅文，禹卫东.基于中国剩余定理解分布式星载SAR－ATI测速模糊［J］.电子与信息学报，2009，31（10）：2493－2497.）

［8］ JIN Guowang.Research on Key Processing Techniques for Accurate DEM Deriving from InSAR［D］.Zhengzhou：Institute of Surveying and Mapping，Information Engineering University，2007.（靳国旺.InSAR获取高精度DEM关键处理技术研究［D］.郑州：信息工程大学测绘学院，2007.）

［9］ ZHANG Hongmin.Research on Data Simulation and Phase Unwrapping for Multi－baseline InSAR［D］.Zhengzhou：Institute of Surveying and Mapping，Information Engineering University，2010.（张红敏.多基线InSAR数据仿真及其相位解缠技术研究［D］.郑州：信息工程大学测绘学院，2010.）

［10］ JIN Guowang，XU Qing，ZHANG Yan，et al.The Zero Intermediate Frequency Vector Filtering for Interferograms［J］.Acta Geodaetica et Cartographica Sinica，2006，35（1）：24－29.（靳国旺，徐青，张燕，等.InSAR干涉图的零中频矢量滤波算法［J］.测绘学报，2006，35（1）：24－29.）

［11］ SHEN Hua，LIU Heguo.Application of Chinese Remainder Theorem on Some Problems［J］.High School Mathematics，2003，12：43－44.（沈华，刘合国.中国剩余定理对几道赛题的应用［J］.中学数学，2003，12：43－44.）

［12］ KENNETH H R.Elementary Number Theory and Its Application［M］.XIA Honggang，trans.Beijing：China Machine Press，2009：104.（KENNETH H R.初等数论及其应用［M］.夏鸿刚，译.北京：机械工业出版社，2009：104.）

Application of Chinese Remainder Theorem in Phase Unwrapping for Dualbaseline InSAR

ZHANG Hongmin1，JIN Guowang1，2，XU Qing1，QIN Zhiyuan1，SUN Wei1
1.Institute of Surveying and Mapping，Information Engineering University，Zhengzhou 450052，China；2.National Key Laboratory of Science and Technology on Microwave Imaging，Institute of Electronics，Chinese Academy of Sciences，Beijing 100190，China

The basic formulation of solving congruence equations with Chinese Remainder Theorem（CRT）is introduced，and CRT is applied to phase unwrapping for dual－baseline InSAR.The congruence equations refer to interferometric phase fuzzy numbers are designed，and the phase unwrapping method for dual－baseline InSAR based on Chinese Remainder Theorem is proposed.In this algorithm，the un－fuzzy phase interval of phase unwrapping is extended，which helps to solve the difficult problem of phase unwrapping in sub－sampling area.The phase unwrapping experiments are done with simulated interferograms from different areas DEMs.The satisfying phase unwrapping results are gotten，as validated the phase unwrapping ability for the proposed algorithm in sub－sampling area.

Chinese remainder theorem；interferometric synthetic aperture radar；multi－baseline；dual－baseline；phase－inwrapping

ZHANG Hongmin（1984—），female，PhD candidate，major in InSAR，photogrammetry and remote sensing.

1001－1595（2011）06－0770－08

TP701

A

国家自然科学基金（40771142；40871213；41071296）；中国博士后科学基金（200801111）；国家西部1∶50 000地形图空白区测图工程项目；测绘学院学位论文创新与创优基金

雷秀丽）

2010－09－25

2010－12－31

张红敏（1984—），女，博士生，主要从事合成孔径雷达干涉测量、摄影测量与遥感技术研究。

E－mail：zhmin1206＠163.com