一类二阶非线性微分方程零解的全局渐近稳定性
2011-01-04张红玲裴新年李宝毅
张红玲,裴新年,李宝毅
(1.天津师范大学 数学科学学院,天津 300387;2.中共天津市委党校 基础课教研部,天津 300191)
一类二阶非线性微分方程零解的全局渐近稳定性
张红玲1,裴新年2,李宝毅1
(1.天津师范大学 数学科学学院,天津 300387;2.中共天津市委党校 基础课教研部,天津 300191)
研究一类二阶非线性微分方程零解的全局渐近稳定性,证明了该系统所有正半轨都是正向有界的,从而得到该系统零解全局渐近稳定的一些条件.推广了相关文献的某些结论,之前较多结果都可由本研究结果推出.
二阶非线性微分方程;零解;全局渐近稳定性;正半轨;正向有界
1 引言及主要结论
考虑一类二阶非线性微分方程

零解的全局渐近稳定性,其中函数φ,F,k,h,ω,g都是R上的连续函数,且满足一定的条件以保证柯西初值问题解的存在唯一性.当k(y)≡1时,系统(1)变为
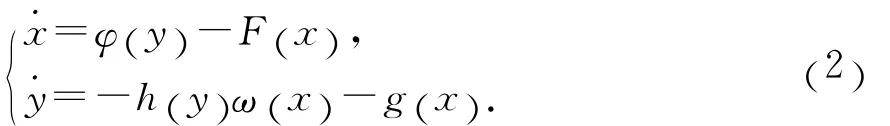
文献[1]给出了系统(2)零解全局渐近稳定的一些条件.系统(1)可看作广义Liénard型方程的进一步推广.关于Liénard型方程解的定性问题已有很多研究,包括解的周期性、振荡性、有界性、稳定性和中心等问题[2-3].本研究在已有成果的基础上对文献[1]进行推广,得到如下结论:
定理1 设则系统(1)的零解全局渐近稳定.

定理2 设

2 主要结论的证明
下面通过3个引理得到以上结论.
引理1 设系统(1)满足如下条件1),2),3)或1),2),3′).


考虑由曲线Γ1和直线x=x1组成的区域Ω1(见图1),可知从点(x0,y0)出发的正半轨线永远停留在区域Ω1内,因此解(x(t),y(t))是正向有界的,故由巴尔巴辛-克拉索夫斯基定理知方程的零解是全局渐近稳定的.

图1 G(+∞)=+∞,G(-∞)<∞时的曲线Figure 1 Curve when G(+∞)=+∞,G(-∞)<∞



图2 G(+∞)<∞,G(-∞)=+∞时的曲线Figure 2 Curve when G(+∞)<∞,G(-∞)=+∞

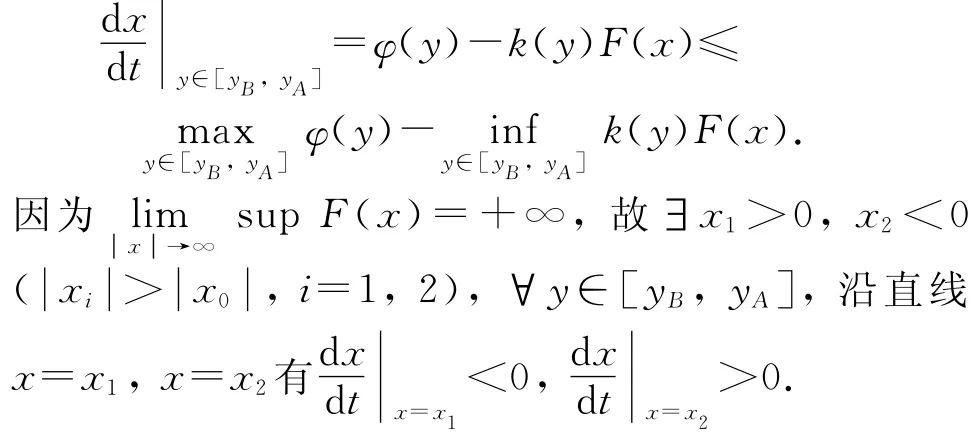
考虑由曲线Γ3和直线x=x1,x=x2组成的区域Ω3(见图3),可知从(x0,y0)出发的正半轨线永远停留在区域Ω3内,因此解(x(t),y(t))是正向有界的,结论成立.

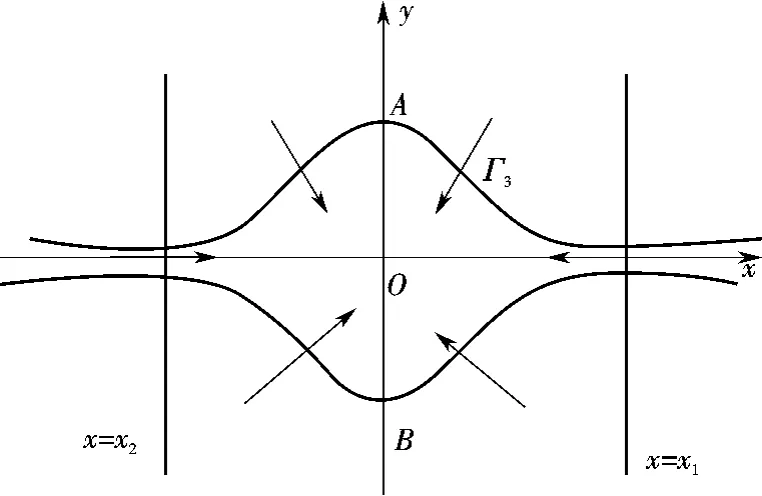
图3 G(+∞)<∞,G(-∞)<∞时的曲线Figure 3 Curve when G(+∞)<∞,G(-∞)<∞

情况2 条件1),2),3′)成立.
当φ(±∞)发散或至少有一个收敛时,同理可以证明结论成立.
引理2 设系统(1)满足如下条件1),2),3)和式(4)或1),2),3′)和式(5).

证明 情况1 条件1),2),3)和式(4)成立.
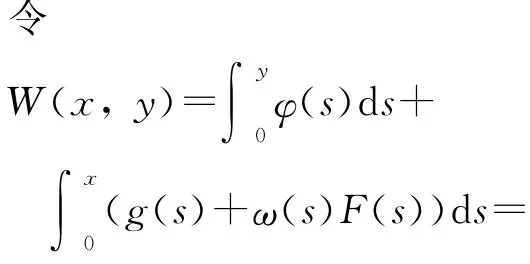


考虑系统(1)从(1,y0)出发的解曲线(x(t),y(t)),可以证明对一切t>0,(x(t),y(t))落在直线y=M之上且不与y=M相交.否则,存在t1>0,使得y(t1)=M,y(t)>M,t∈[0,t1),于是∀t∈[0,t1),有


[1] Zhao L Q.On global asymptotic stability of trivial solution for a class of second order differential equations[J].Advances in Mathematics,2006,35:378-384.
[2] 李惠卿.Liénard方程零解全局渐近稳定的充要条件[J].数学学报,1988,31(2):26-32.
[3] 刘正荣.Liénard方程全局稳定性的条件[J].数学学报,1995,38(5):614-620.
[4] Zhou J.Boundedness and convergence of a second order nonlinear differential system[J].Journal of Mathematical Analysis and Applications,2001,256:360-374.
[5] 赵丽琴.一类微分方程零解全局弱吸引和全局吸引的充要条件[J].数学物理学报,2009,29A(3):529-537.
[6] 张芷芬,丁同仁.微分方程定性理论[M].北京:科学出版社,1985.
[7] 高素志.二阶非线性微分方程零解的全局渐近稳定性[M]//焦善庆.数学、物理、力学高新技术研究进展.成都:西南交通大学出版社,1996:6-7.
[8] 严平,蒋继发.Liénard系统零解的全局渐近稳定性[J].安徽师范大学学报:自然科学版,1999(2):16-18.
[9] Wang D S,Tan Y S.Asymptotic stability in the large of zero solution of second order nonlinear differential equations[J].Chinese Quarterly Journal of Mathematics,2001,16(2):13-16.
Global asymptotic stability of zero solution for a class of second order nonlinear differential equations
ZHANGHongling1,PEIXinnian2,LIBaoyi1
(1.College of Mathematical Science,Tianjin Normal University,Tianjin 300387,China;
2.Department of Basic Courses,Party School of CPC Tianjin Municipal Committee,Tianjin 300191,China)
The global asymptotic stability of the zero solution for a class of second order nonlinear differential equations is studied.Some sufficient conditions and a necessary condition are obtained by proving that all the positive semi-orbits of the system are positively bounded.Some results of relevant literatures are extended and some previous results can be obtained from this paper's results.
second order nonlinear differential equations;zero solution;global asymptotic stability;positive semiorbit;positivelybounded
O175.1
A
1671-1114(2011)03-0013-04
2010-09-30
张红玲(1986—),女,硕士研究生.
李宝毅(1963—),男,教授,主要从事常微分方程定性理论及其应用方面的研究.
(责任编校 马新光)
