一类基于时滞和年龄分布的非线性种群系统解的唯一性

管文文，赵 春

（天津师范大学 数学科学学院，天津 300387）

一类基于时滞和年龄分布的非线性种群系统解的唯一性

管文文，赵 春

（天津师范大学 数学科学学院，天津 300387）

研究一类基于时滞和年龄分布的非线性种群系统，其状态方程由一阶偏泛函微分方程描述.利用不动点定理得到了系统解的存在唯一性.

种群模型；时滞；年龄结构

生物种群系统解的存在唯一性一直是人们十分关心的问题，关于年龄分布的种群系统，已有学者做了大量的研究，并积累了较为丰富的研究成果.文献［1］研究了依赖年龄的单种群动力系统非线性模型解的存在唯一性问题.而在种群演化过程中，时滞是客观存在的因素，因此较为合理的种群模型应当考虑时滞因素的影响.文献［2］研究了基于时滞和年龄分布的齐次模型，证明了解的存在唯一性.本研究在此基础上考虑非齐次模型解的存在唯一性问题.

本研究提出如下数学模型：

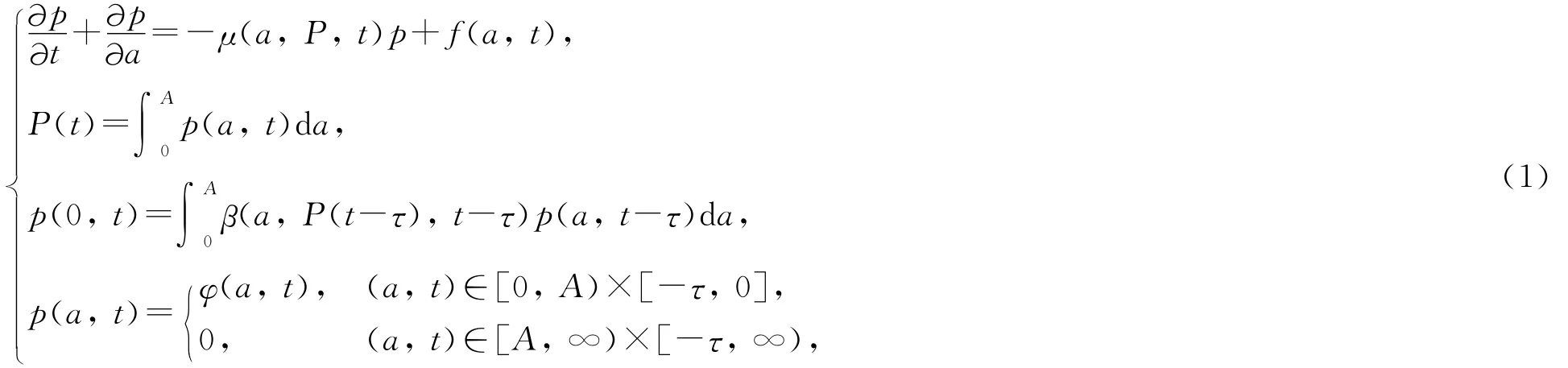
其中，A表示个体最高寿命，状态变量p（a，t）表示时刻t年龄为a的种群个体密度，常数τ＞0表示孕育期，函数μ，β，φ分别表示个体平均死亡率、出生率、初始时间段上的种群个体分布，f（a，t）表示转移人口的数量，P（a，t）表示种群总的数量.

本研究假设：

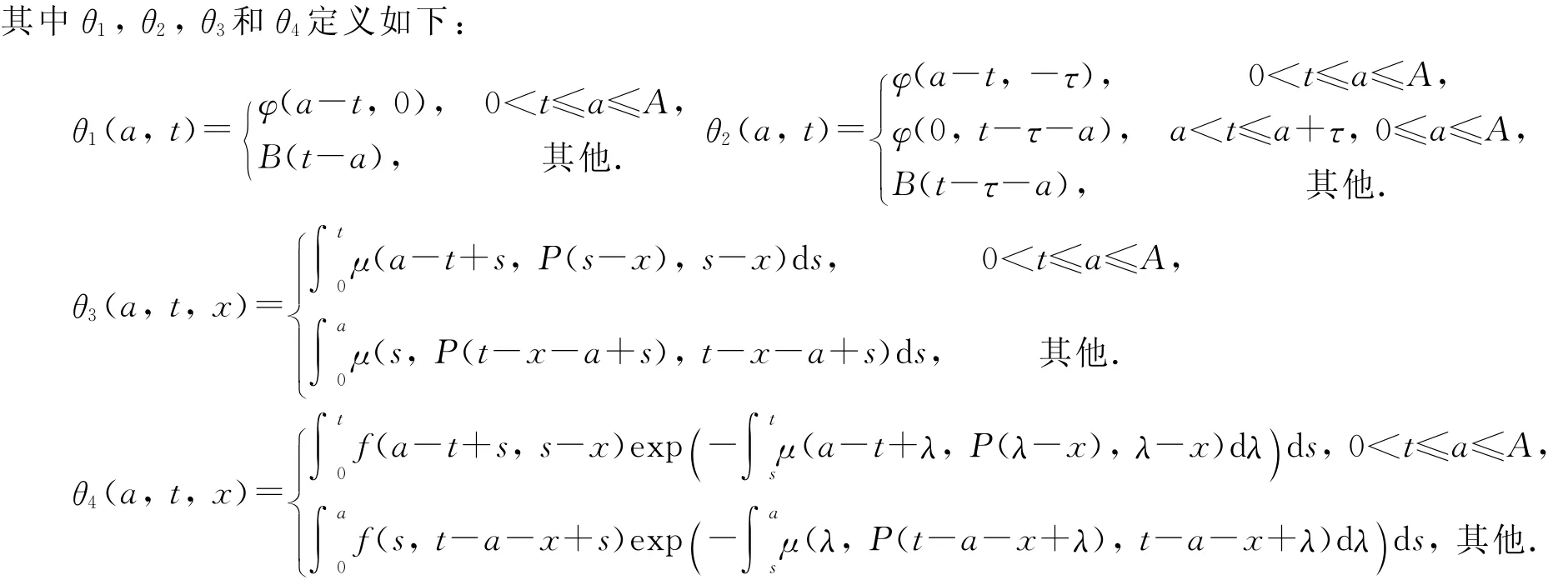
引理 如果p是系统（1）的解，那么P（t）和B（t）在［0，T］上满足式（7）—（8）.如果P（t）和B（t）满足式（7）—（8），且是连续非负函数，那么p是系统（1）的解.

定理 如果条件（H1）和（H2）成立，那么系统（1）存在唯一非负解.

证明 只需证明P（t）和B（t）有唯一解即可，再由引理则可知系统（1）存在唯一非负解.

因为τ＞0，且φ（a，t）已知，则当0≤t≤τ时，B（t）可由式（8）直接求出.首先定义C＋（γ）＝C［［0，γ］，R＋］，其中0≤γ≤τ.设g∈C＋（γ），令

［1］ Gurtin M E，Maccamy R C.Non－linear age－dependent population dynamics［J］.Arc Ratinal Mech Anal，1974，54：281－300.

［2］ 何泽荣.一类基于时滞和年龄分布的种群控制问题［J］.系统科学与数学，2010，30（1）：53－59.

［3］ Swick K E.A nonlinear age－dependent model of single species population dynamics［J］.SIAM J Appl Math，1977，32（2）：484－498.

［4］ Cushing J M.Model stability and instability in age structured populations［J］.J Theor Biol，1980，86：709－730.

Uniqueness of solution for a class of nonlinear population systems with time delay and age distribution

GUANWenwen，ZHAOChun
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

A class of nonlinear population systems with time delay and age distribution is studied，whose state system is described by apartial functional differential equation.The uniqueness of solution for the system is proved by means of fixed point theorem.

population model；time delay；age distribution

O175.1

A

1671－1114（2011）03－0001－04

2010－12－05

国家自然科学基金资助项目（60972089）；天津市高等学校科技发展基金计划资助项目（20060401）；天津师范大学博士科研启动基金资助项目（5RL047）

管文文（1984—），女，硕士研究生.

赵 春（1963—），男，教授，主要从事控制论及其应用方面的研究.

（责任编校 马新光）