基于有限元法进行人体腓肠肌振动模型仿真研究

张海岛,闵一建,刘新元,龙娇群

基于有限元法进行人体腓肠肌振动模型仿真研究

张海岛1,2,闵一建1,2,刘新元1,2,龙娇群3

研究腓肠肌振动频谱分布规律,利用有限元软件ANSYS建立腓肠肌振动模型,计算腓肠肌提踵时振动的固有频率及振型,并使用专门的肌声检测系统测量10名大学男生负重提踵时的腓肠肌肌声信号。模拟结果显示,腓肠肌的振型随频率的增大存在一定的分布规律,实验测量表明振动的能量主要集中在超低频区。将模拟结果与实验数据进行对比分析,表明能量集中在超低频区的振型主要有4种。

有限元法;腓肠肌;振动模型

1 引言

骨骼肌是构成人体的重要组织,约占体重40%。骨骼肌的功能是收缩躯体运动,包括体育运动中各式各样的运动动作,都是由骨骼肌的收缩来实现的[1]。因此,骨骼肌的生物力学研究历来是国内外科学家研究的重点,其研究成果对于运动训练、恢复治疗以及自动控制的理论研究有积极的意义。研究骨骼肌力学特性,建立力学模型是一种很重要的途径。但是,由于模型的理论表达、物体的几何形状以及载荷作用方式很复杂,求解一般是非常困难,甚至是不可能的,惟一的方法就是应用数值法,求得近似解。作为数值法的一种,有限元法是一种将连续体简化为有限个单元组成的离散化模型,再对离散化模型进行求解的数值方法,由于其物理概念清晰,灵活性和实用性强的特点,被逐渐地运用到骨骼肌的力学分析中。国外学者Hatze在1981年提出的由多个集中参数模型联合组成的肌肉模型被认为是肌肉有限元模型的先驱[10];Van Leeuwen将骨骼肌中的应力描述为主动、被动应力之和,并试图将主动行为这个概念引入类似肌肉的材料中[13];Johansson考虑骨骼肌为纤维增强复合材料,导出关于骨骼肌的大形变、超弹性本构关系,得到形变与应力分布规律[14];Kojic等将Hill模型的串联弹簧发展为非线性模型,采用多重并联模型描述骨骼肌性能,开发了计算肌肉模型的专用有限元软件PAK,用于肌肉疲劳计算[2,8]。此类研究的主要特点是通过建立骨骼肌的近似模型模拟骨骼肌的机械力学行为,利用有限元软件预测骨骼肌的应力、应变分布及形变的规律。但是,有关以声学振动方式研究肌肉的振动模态未见文献报道。

本文以骨骼肌的机械振动为研究对象,着重研究腓肠肌振动模态,通过有限元软件ANSYS建立腓肠肌的数值模拟,结合实验测得的骨骼肌振动信号,探讨腓肠肌运动态的振动规律。

2 仿真模型的建立

人类的小腿后部肌肉特别发达,这是由于此肌群对维持人体直立姿势有关,特别是小腿三头肌更是发达。腓肠肌是小腿三头肌的一部分,位于小腿后群肌最浅层,与比目鱼肌形成小腿肚。在近固定时,屈膝关节,并能使足在踝关节处跖屈;远固定时,和比目鱼肌拉股骨后端和小腿骨向后,使膝关节伸直,维持人体直立[4]。因此,它对运动起着至关重要的作用。

图1 腓肠肌模型示意图Figure 1. Gastrocnemiusmodel

腓肠肌有内外两个头,外侧头、内侧头分别起自股骨头外上髁和内上髁,由两头起的肌束向下,于小腿中部相互愈着,移行于较厚的腱膜,再与比目鱼肌腱膜愈着,构成跟腱[3]。由于腓肠肌的外部轮廓不规则,有限元模型的外形通过实际测量健康男性小腿外围尺寸与表面皮脂厚度,并假设皮脂层厚度均匀,测得具体平均尺寸,得到关键点之间的相对位置,结合腓肠肌一般尺寸,利用ANSYS软件中的B-splines方法生成。腓肠肌的一般尺寸来自《中国人解剖学数值》:腓肠肌全长为39.64±3.65 cm,腓肠肌内侧头肌腹长22.30±3.43 cm,宽6.10±1.89 cm,厚1.12 ±0.32 cm。外侧头长20.82±4.53 cm,宽5.56±1.75 cm,厚0.82±0.37 cm,跟腱长17.58±2.40 cm,宽1.37± 0.3 cm[6,7]。建立的腓肠肌模型的长度方向为Y轴,宽度方向为X轴,厚度方向为Z轴。图1模型采用8节点单元SOL ID45,设腓肠肌材料各向同性,材料性能参数为:杨氏模量E=2.12 KPa,泊松比=0.4999,密度=1 000 kg/ m3[9,11]。

3 腓肠肌的模态计算与分析

根据弹性力学的有限元法,系统的运动微分方程如下式所示:

时自由振动时阻尼对其模态频率及振型的影响很小,通常忽略。此时方程表到为:

其对应的特征方程为:

式中,ω为自然圆频率。求得圆频率后,将其代入方程,求得对应的特征向量u,对应于振动频率ω的主振型。当n个主振型汇集在一个方阵内,该方阵的每一列代表着各个主振型,此方阵被称为振型矩阵。

结构系统的振动,主要是求解系统的动力学方程(1),以求得系统产生的位移、速度和加速度的值。常用的解法有振型法和直接积分法。振型法首先利用自由振动的振型矩阵对系统的动力学方程进行解耦处理,以得到各自独立的动力学方程,然后进行分别求解;直接积分法就是直接将动力学方程对时间进行分段数值离散,然后计算每一时刻的位移的数值。Ansys的模态分析就是结合有限元方法与上述理论,用来确定结构或部件的振动特性的。

模态就是结构振动时所具有的基本振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。每一个模态代表的是一个单自由度系统的振动。对于多自由度系统,振动可以分解为单自由度的振动的叠加,也就是说,系统不是做某一固有频率的振动,而是做多个固有频率的简谐振动的合成振动。用ANSYS对腓肠肌模型进行模态分析,模拟腓肠肌近固定时的运动,探究腓肠肌提踵时的振动规律。根据腓肠肌运动时收缩的实际情况,在模型近端施加零位移约束,在内表面施加横向约束,远端施加非轴向约束;腓肠肌运动时受轴向的力,在模拟时通过静力分析把预应力计算出来加到结构上。力是以应力的形式施加于模型末端的平面,大小为外载荷与小腿下端截面积的比值为34 KP。利用提取的模态分析腓肠肌振动特征,发现其前20阶模态阶数与对应固有频率及振型在超低频范围(表1)。

其中,第1～5阶为刚体振型,它们在物理结构中的激活不是弹性力,故略去不计。

图2给出腓肠肌在低频下的4个具有代表性的振动模态,分别是Z轴方向弯曲、Y轴方向伸缩、X轴方向弯曲和扭曲振动。

4 肌肉振动数据的测量、采集与处理

肌声是肌肉运动时由于肌肉的机械振动发出的声波,是一种微弱的低频声信号[5]。因此,有效采集肌肉的声信号是关键。使用陕西师范大学声学研究所专门的肌声检测系统[12]对信号进行拾取和分析。检测系统的硬件平台是由声电换能器、高性能数据采集器以及计算机组成。使用声电换能器采集肌声信号,将信号经放大器处理,传输到数字采集器进行采集、数字化,并把信号传输到计算机上,最后在计算机上对信号进行FFT分析处理。

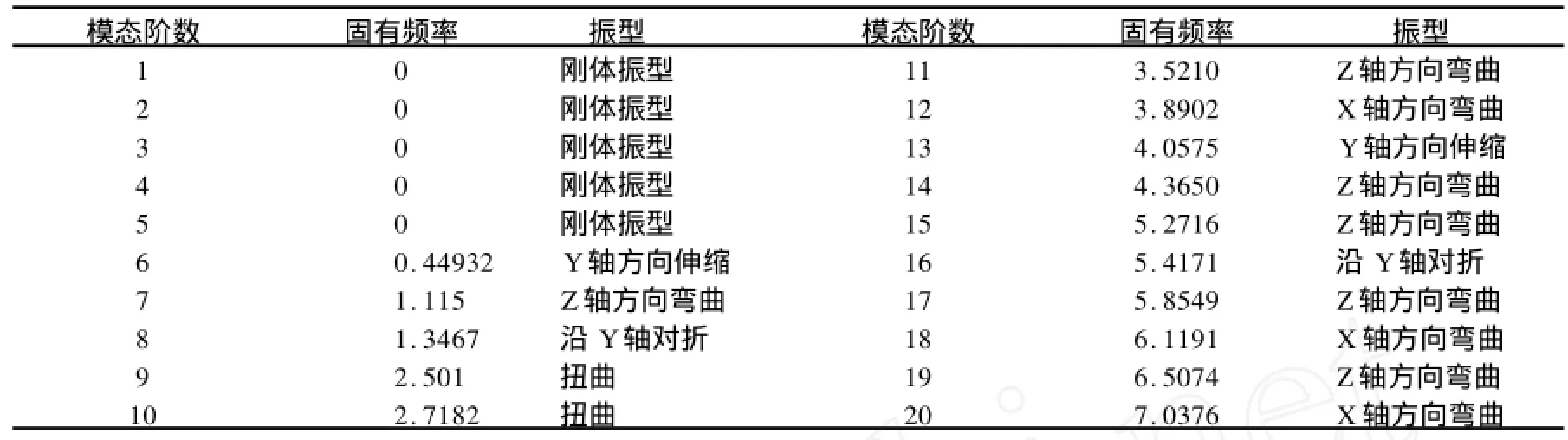
表1 本研究腓肠肌振动前20阶固有频率及振型一览表Table 1 The First 20 Natural Frequency and Major Shapes of the Gastrocnemius

图2 腓肠肌典型振动模态示意图Figure 2. Typical Vibrational Model of the Gastrocnemius

测试对象为陕西师范大学物理学与信息技术学院2006级身体健康的男学生10名,24 h之内未参加过剧烈运动。利用多功能健身器(Torus408美国),使用直立恒定负重提踵的运动方式,负重为13.50 kg,手握负重,按照预先设定的节拍垂直提踵。采集信号的传感器固定于腓肠肌外侧头肌腹处。图3、图4分别为其中一名被测试人员的时域及频域腓肠肌声图。

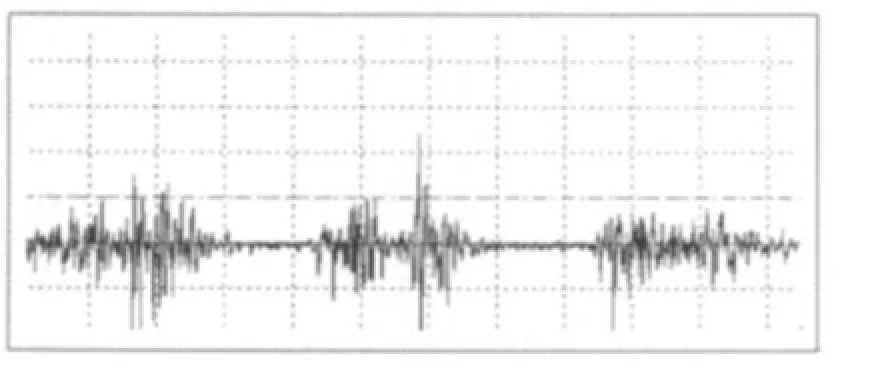
图3 腓肠肌声信号时域图Figure 3. The Time-domain Diagram of the Acoustic Signal of the Gastrocnemius

图4 腓肠肌声信号FFT频域图Figure 4. The Frequency-domain Diagram of the Acoustic Signal of the Gastrocnemius

表2 本研究小腿腓肠肌声频谱统计一览表Table 2 Statistical Table of the Frequency Spectrum of the Gastrocnemius (Hz)

将测试获得的腓肠肌声频域谱进行统计分析处理(表2)。从表2可以看出,受试者在提踵测试时,肌声频率范围在1.5672±1.205 Hz～45.927+9.057 Hz,主峰频率平均值在7.672±1.903 Hz,主能量区范围在5.218± 2.324 Hz～11.0896+5.291 Hz。

5 分析与讨论

从模态分析得到的结果可以看出,腓肠肌各阶模态的振型随着频率的增大有一定的变化规律。阶次低的模态振型是以Z轴方向弯曲振动和Y轴方向伸缩振动为主,随着频率的增大,X轴方向弯曲振动成为主要的振型,其次是扭曲振动,但所占比例很少。其他振型无规律的分布在这两种振动之间。

振动时的振型和运动时物体受到的边界条件及初始条件有关。测试人员在进行负重提踵测试时,腓肠肌沿轴向收缩使踝关节跖屈,肌肉沿Y轴方向运动,力作用的方向主要在Y轴,在这样的条件下,腓肠肌的扭曲振动在肌肉做伸缩运动时受到一定程度的限制,主要振动是Y轴方向伸缩振动和小幅度(低阶)Z轴方向弯曲振动。虽然腓肠肌振动的频带较宽,但能量集中在超低频区,峰值频率基本在10 Hz以下。数值模拟腓肠肌振动的固有频率与实验测量的结果主峰频率比较接近,揭示了腓肠肌在超低频区的振动模态是Y轴方向伸缩振动和Z轴方向弯曲振动为主。

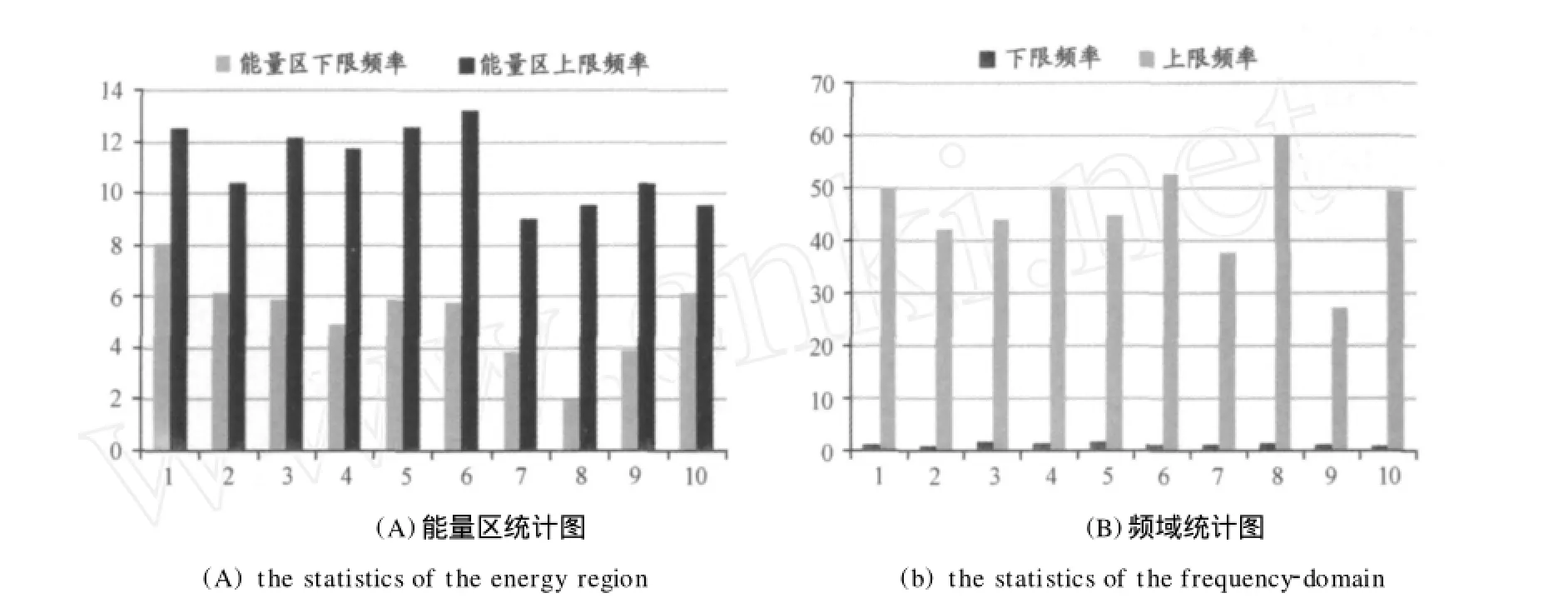
图5 腓肠肌频域及能量区统计示意图Figure 5. The Statistical Diagram of the Frequency-domain and the Energy Region of the Gastrocnem ius

6 结论

本文使用有限元软件ANSYS建立了腓肠肌三维振动模型,利用软件计算得到了腓肠肌近固定时振动固有频率和相对应的振型,计算结果显示,在不同的频段腓肠肌振型有一定的分布规律。通过FFT测量分析得到负重提踵时腓肠肌的肌声信号,频谱显示腓肠肌振动的能量主要集中在5.22±2.32 Hz～11.09±5.29 Hz的超低频区。对比分析数值计算和实验测量结果,发现与能量集中的低频区所对应的振型是在腓肠肌受轴向力是容易激发的Z轴方向弯曲与Y轴方向伸缩。研究结果表明,建立的数值模型可以描述腓肠肌振动的频率特性。通过声学振动的方法研究腓肠肌生理与运动特征,可以为肌肉力量训练研究提供肌声测试方法和理论依据,使运动训练手段的选择更加科学有效。

[1]邓树勋,王健,乔德才.运动生理学[M].北京:高等教育出版社, 2005:33.

[2]龚亚琦,樊建平.基于纤维增强超弹性基体模型的骨骼肌有限元模拟[J].中国生物医学工程学报,2009,28(5):792-796.

[3]河北新医大学《人体解剖学》编写组.人体解剖学[M].北京:人民卫生出版社,1977:473-477.

[4]李月玲.卫星电视教育、教育学院、函授、自学通用运动解剖学[M].北京:高等教育出版社,1987:183-187.

[5]闵一建,赵春燕.原动肌与协同肌在运动中的作用[J].中国现代临床医学,2005,4(3):18-19.

[6]王沫楠,张猛.基于有限元法人体腿部生物力学仿真研究[J].系统仿真学报,2008,20(20):5638-5641.

[7]中国解剖学会体质调查委员会.中国人体解剖学数值[M].北京:人民卫生出版社,2000:134.

[8]C Y TANG,C P TSU I,B STOJANOV IC,et al.Finite element modelling of skeletal muscles coup led w ith fatigue[J].Int J M echanical Sci,2007,49:1179-1191.

[9]ERIC J CHEN,JAN NOVAKOFSKI,W KENNETH JENKINS,et al.Young’s modulus measurements of soft tissues with application to elasticity imaging[J].IEEE Transactions On U ltrasonics,Rerroelectrics,and Frequency Control,1996,43(1) :191-194.

[10]HA TZE H.M yocybernetic control models of skeletal muscle: Characteristics and app lication[M].Preto ria:Univesity of Sou th A frica,1981:201-211.

[11]HERZOG W.(ed.).Skeletal muscle mechanics:f rom mechanisms to function[M].New York:John Wiley&Sons,2000: 207-224.

[12]M YI-JIAN,W SHENG-JU,Q TIE-QUN,et a l.Research of themusclemotive characteristic based on sound spectrum technology Science and technology for social and economic development:Toward the 21century[M].Zguang-zhao chief editor Beijing:China Science Technology Press,1999:858.

[13]VAN LEEUW EN J L.Op timum pow er output and structru ral design of sarcomeres[J].J Theoretical Biology,1991,149:229-256.

[14]Y L IANG,R M MCMEEKING,A G EVANS.A finite element simulation scheme fo r biological muscular hydrostats[J].J Theoretical Biology,2006,242:142-150.

Simulation of Vibrational Model of the Gastrocnem ius Based on the Finite Elemen t Method

ZHANG Hai-dao1,2,M IN Yi-jian1,2,L IU Xin-yuan1,2,LONG Jiao-qun3

In this paper,natural frequency and majo r shapes of the gastrocnem ius at heel raised are calculated w ith the vibrational model of the gastrocnemius established by ANSYS.In addition,acoustic signal of the gastrocnem ius at heel raised w ith heavy load of 10 male students are measured w ith specialized sound detection system.The result show s that the majo r shapes regulate to the increase of the natural frequency.Further mo re,the energy of the vibration observed in the experiment is largely concentrated in low-frequency.Comparing w ith these results,it indicates that the majo r shapes w here the energy of the vibration is concentrated in super low-frequency mainly have four types.

the finite element;gastrocnem ius;vibrationa lm odel

G804.6

A

1000-677X(2011)01-0044-04

2010-11-08;

2010-12-16

国家自然科学基金资助项目(10974129)。

张海岛(1985-),男,内蒙古人,硕士研究生,研究方向为运动声学,E-mail:262268197@qq.com;闵一建(1953-),男,福建莆田人,副教授,硕士研究生导师,研究方向为生物声学与信号处理,E-mail:minyj@snnu.edu.cn。

1.陕西师范大学应用声学研究所,陕西西安710062; 2.陕西省超声学重点实验室,陕西西安710062;3.陕西师范大学物理学与信息技术学院,陕西西安710062 1.Instituteof Applied Acoustics,Shanxi No rmal University,Xi’an 710062,China;2.Key Lab of A coustics,Xi’an 710062,China;3.College of Physics and Information Technology,Shanxi No rmal University,Xi’an 710062, China.