基于ABAQUS 的粘弹性动力人工边界精确自动施加

徐 磊 叶志才 任青文 杜小凯

(1.河海大学水利水电工程学院, 南京 210098;2.河海大学土木工程学院, 南京 210098;3.宿迁市水务局, 江苏宿迁 223800;4.中国水电工程顾问集团公司, 北京 100120)

在对结构-地基动力相互作用问题的计算分析中,如何考虑无限地基的辐射阻尼效应是核心问题之一[1].若人工截取有限区域地基来模拟无限地基,则会使得散射波在人工截取的边界上产生反射而导致模拟失真.目前,在截取的有限域边界上设置合理的动力人工边界条件是解决这一问题的有效方法[2].近年来,相关学者已提出了多种动力人工边界条件,如粘性边界、旁轴近似边界、透射边界和粘弹性边界等[3].其中,粘弹性动力人工边界[4]以其精度较高、能模拟人工边界外半无限介质弹性恢复性能且有良好的频率稳定性而在结构-地基动力相互作用问题的有限元分析中得到了广泛的应用.

对于实际工程中的结构-地基动力相互作用有限元分析,一般均需采用三维计算模型,随着工程仿真建模的日益精细化,有限元分析模型存在大量的边界结点,数量通常可以达到数千甚至更多.当采用粘弹性动力人工边界时,由于各边界结点与散射波源(结构)之间距离不等、各结点所控制的边界面积不等以及各点所在区域的地基材料也会有所差别,因而,对于各边界结点,需逐点计算其弹簧系数及阻尼系数并施加弹簧单元及阻尼器单元,有限元前处理工作量浩繁.为了便于处理,通常采用一些近似方法来进行粘弹性边界的施加,如各边界结点取散射波源至其所在人工边界面的平均距离作为其与散射波源实际距离的近似等[5],这些近似势必会对边界条件的精度造成一定程度的影响.

为此,基于粘弹性动力人工边界理论大型商用有限元软件ABAQUS,开发相关程序,实现了对粘弹性动力人工边界的精确自动施加.算例分析验证了程序的合理性和有效性.此外,还将本文方法和通常的近似施加方法进行了对比分析,结果表明,近似施加方法会引起较大计算误差,本文所提出方法的施加简便性、施加精度均优于通常的近似施加方法.

1 粘弹性动力人工边界

粘弹性动力人工边界可以等效为在计算模型截断边界上连续分布的并联弹簧-阻尼器系统,其中,弹簧系数Kb及阻尼系数Cb的计算公式如下:

式中,G、ρ分别为人工边界处介质的剪切模量、密度;R 为散射波源至人工边界的距离;c 为人工边界处介质的波速,法向阻尼系数取为纵波速cp,切向阻尼系数取为剪切波速cs;α的取值取决于粘弹性动力人工边界的类型及设置方向,见表1.

表1 α的取值

粘弹性动力人工边界是一种连续分布的人工边界条件.当采用有限元法将计算区域离散化后,连续的人工边界面也随之离散化,此时,在有限元计算模型中,为了实现粘弹性动力人工边界的施加,需要在边界结点的法向和切向分别设置并联的弹簧单元和阻尼器单元,相应的弹簧系数K 和阻尼系数C 除了与式(1)有关外,还与边界结点的等效控制面积相关,计算表达式如下

式中,Gi、ρi、ci及Ai分别为与边界结点相关联单元的材料物理力学参数及面积.

对于实际工程问题,由于有限元计算分析模型的边界结点数量众多,且需逐点按式(2)计算其弹簧系数及阻尼系数并施加弹簧单元及阻尼器单元,有限元前处理工作十分困难,若采用近似处理又难免引入误差.为此,在上述基础上,基于ABAQ US 编制了用于粘弹性动力人工边界精确自动施加的fortran 程序.

2 粘弹性动力人工边界精确自动施加

近年来,作为国际上最先进的大型通用商业非线性有限元分析软件之一,A BAQ US 在结构-地基动力相互作用等问题中的应用日益广泛[6].ABAQUS 中的弹簧阻尼器单元也为施加粘弹性动力人工边界提供了方便.此外,用户还可以通过二次开发接口[7]或编程读写input 计算文件等方式实现更为复杂的计算功能.为此,基于粘弹性动力人工边界理论以及ABAQ US 的input 计算文件的相关格式,编制了用以实现粘弹性动力人工边界精确自动施加的fortran程序.该程序在获取有限元计算模型相关信息的基础上,直接生成用以施加粘弹性动力人工边界的命令文本,该文本完全符合input 计算文件的相关格式,将其放入相应input 文件的指定位置即可完成基于ABAQ US 的粘弹性动力人工边界精确自动施加.

为了实现粘弹性动力人工边界精确自动施加,首先需要完成有限元计算模型的网格剖分、材料分区等,在此基础上,获取所需的有限元网格的结点坐标、各单元的结点编号及其材料号、需要施加粘弹性动力人工边界的边界结点编号、各边界结点所在边界面的法线方向以及散射波源位置等信息.

在上述基础上,编制了相应的fortran 程序,实现了基于ABAQUS 的粘弹性动力人工边界条件精确自动施加,图1 给出了相应的程序流程图.

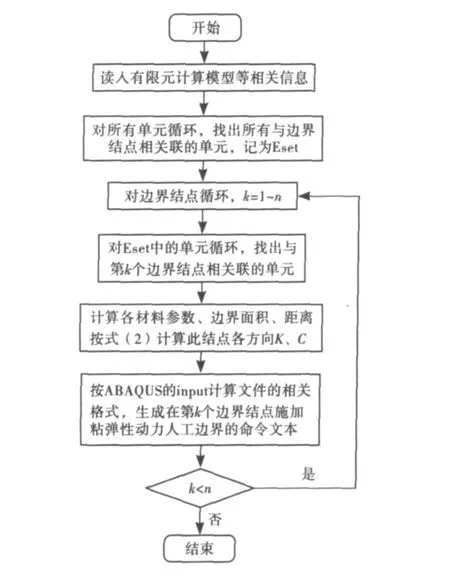
图1 程序流程图

下面对程序中较为关键的问题进行扼要的说明,首先是如何计算关联单元边界面(即位于截断边界上的单元面)的面积,一般而言,与某一边界结点相关联的单元有多个,对任一关联单元,可首先依据单元各结点坐标与边界结点坐标之间的关系,并结合边界结点所在面的法向来确定在单元边界面的所有结点.其次是如何计算单元边界面的面积,对于二维问题,边界面的面积计算实质上是计算两点间线段的长度,易于解决;对于三维问题,单元边界面形状一般为三角形或四边形,对于三角形,依其顶点坐标容易计算其面积,而对于四边形,当只知其4 个顶点坐标而不知其顶点顺序时,无法应用通常的四边形面积公式进行求解,此时,可先应用海伦公式计算由此4 个顶点中任意3 个顶点所确定的4 个不同三角形的面积,则四边形面积即为这4 个三角形面积之和的一半.需要说明的是,以上关于面积计算的说明中仅考虑不含中结点的单元,对于非此类单元,一般均可将其单元形态近似为不含中结点的单元来加以处理.

3 算例验证及对比分析

为了验证2 中所编程序的正确性和有效性,进行了如下算例分析.

考虑半无限空间z ≥0,分析模型如图2 所示,人工截取计算区域取为|x|≤10 m 、|y|≤10 m、|z|≤10 m.模型介质的物理力学参数如下:弹性模量E =50 MPa;泊松比v=0.3;剪切波速cs=83.62 m/s;纵波速cp=156.48 m/s;密度ρ=2 750 kg/m3.为了便于对计算成果进行分析,在分析模型上设置了2 个观察点A、B,其坐标分别为(0,0,10),(5,0,10).在自由面上沿z 方向加一集中面源(作用范围为-5 m ≤x ≤5 m,-5 m ≤y ≤5 m,z=10 m)时变荷载f(t), f(t)的函数表达式如式(3)所示.

式中,0 ≤t ≤2 s.

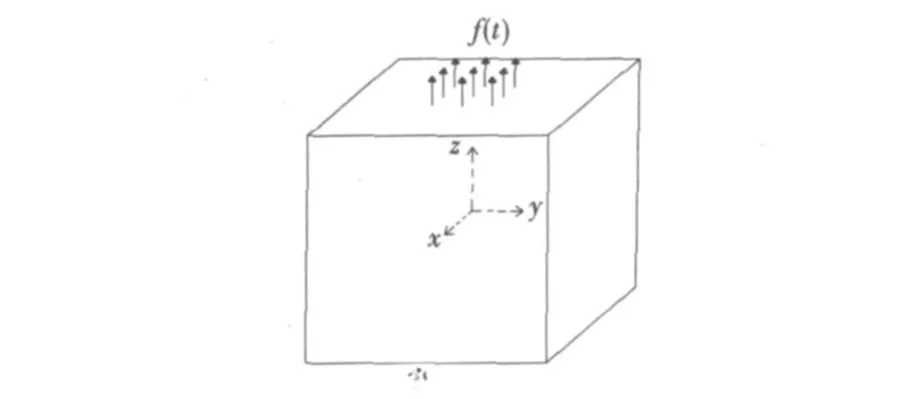
图2 算例分析模型

采用8 结点六面体单元进行网格剖分,有限元模型如图3 所示,网格尺寸Δx=Δy =Δz=1 m,散射波源取为荷载作用面的中心.在截断边界上,采用节2中编制的fortran 程序实现粘弹性动力人工边界的精确自动施加,记为C.B.;为了对比分析本文方法与通常近似方法之间的差别,还采用了后一方法对上述算例进行了粘弹性边界的施加,在施加过程中,各边界结点取散射波源至其所在人工边界面的平均距离作为其与散射波源实际距离的近似,记为A.B.;此外,还给出了远置粘弹性动力人工边界(本文采取在模型各个方向均扩大20 倍范围后设置人工边界的方法)的有限元解作为精确解,记为E.B..

图3 有限元计算网格图

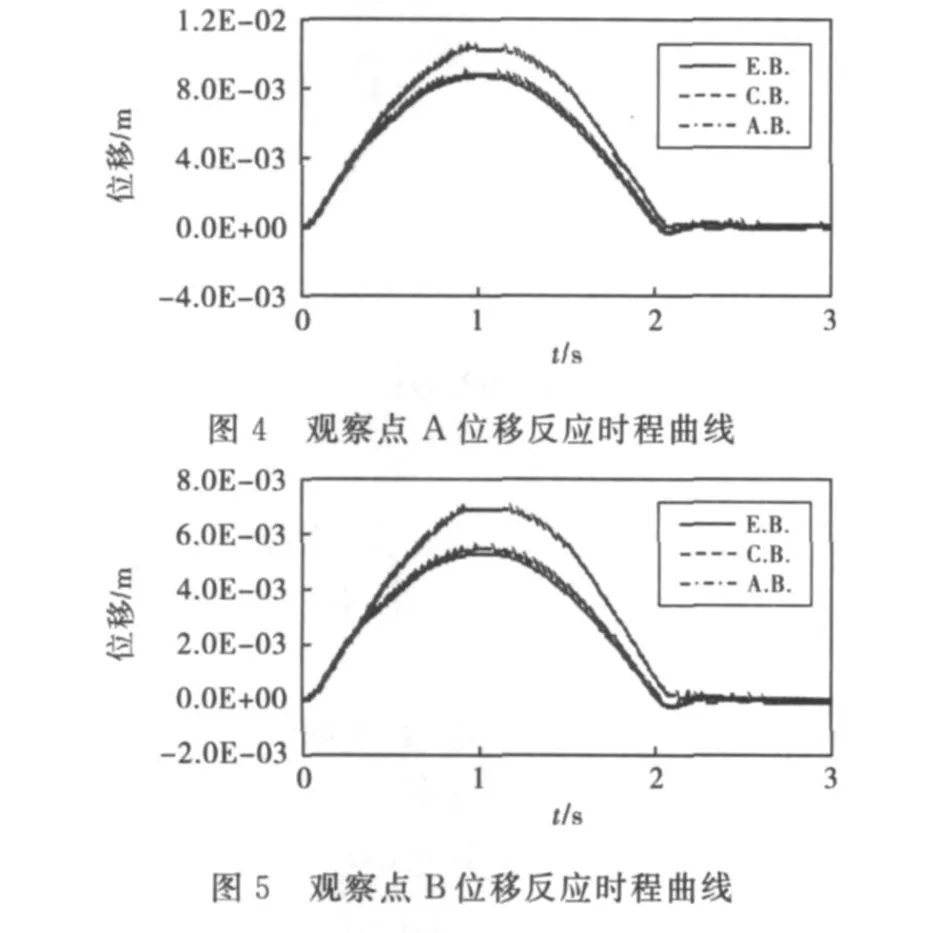
动力时程分析的时间步长取为0.01 s,计算总时长为3 s.图4 ～5 给出了观测点A、B 在不同边界条件下的z 向位移反应时程曲线.从中可以看出,与精确解相比,本文所提出的粘弹性动力人工边界精确自动施加方法(C.B.)与近似施加方法(A.B.)均可以给出与精确解(E.B.)总体趋势一致的计算结果,但也可明显发现,C.B.方法所给出的计算结果与A.B.方法所给出的计算结果相比,与精确解更为一致,而A.B.方法所给出的计算结果与精确解相比有较大误差,这是由于其在设置粘弹性动力人工边界时所采用的简化近似处理而造成的.以上分析表明,本文所提出的粘弹性动力人工边界精确自动施加方法在计算精度上相比通常的近似施加方法有明显的优势,可以给出更为精确的计算结果,此外,由于本文所提出方法为自动施加,其在施加速度上较通常近似施加方法也有明显的优势,尤其是对于计算规模较大、边界结点较多的结构与地基动力相互作用分析问题.

4 结 语

在结构-地基动力相互作用问题的有限元分析中,粘弹性动力人工边界得到了广泛的应用.但对于规模较大的复杂计算模型而言,粘弹性动力人工边界的施加存在着前处理工作量浩繁、施加精度不高等问题.为此, 本文基于粘弹性动力人工边界理论及ABAQ US 软件平台,提出了粘弹性动力人工边界精确自动施加方法,编制了相关程序并进行了验证.算例将本文方法和通常的近似施加方法进行了对比分析,结果表明,近似施加方法会引起较大计算误差,本文所提出方法的施加简便性、施加精度均优于通常的近似施加方法.

[1] 刘晶波, 谷 音,杜义欣.一致粘弹性动力人工边界及粘弹性边界单元[ J] .岩土工程学报, 2006, 28(9):1070-1075.

[2] 刘晶波,王振宇,杜修力等.波动问题中的三维时域粘弹性动力人工边界[ J] .工程力学,2005,22(6):46-51.

[3] 廖振鹏.工程波动理论导论[ M] .2 版.北京:科学出版社, 2002.

[4] Deeks A J, Randolph M F.Axisymmetric Time-domain Transmitting Boundaries[ J] .Journal of Engineering Mechanics, 1994,120(1):25-42.

[5] 张燎军,张慧星, 王大胜等.黏弹性人工边界在ADINA中的应用[ J] .世界地震工程,2008,24(1):12-16.

[6] 庄海洋,陈国兴,胡晓明.两层双柱岛式地铁车站结构水平向非线性地震反应分析[ J] .岩石力学与工程学报,2006, 25(S1):3074-3079.

[7] 叶志才, 徐 磊,王 超.基于ABAQUS 的三维锚杆单元开发[ J] .三峡大学学报:自然科学版, 2008, 30(5):29-32.