基于离散指数函数优化GM(1,1)模型的重新优化

2010-08-02陈鹏宇段新胜

三峡大学学报(自然科学版) 2010年1期

陈鹏宇段新胜

(中国地质大学(武汉)工程学院,武汉 430074)

灰色预测模型是灰色理论的重要组成部分,而GM(1,1)模型是灰色预测模型中最基本的预测模型,已经在许多领域得到了广泛应用[1-3].但是GM(1,1)模型在许多情况下预测精度并不高,即使拟合纯指数序列也得不到满意的结果,因此一些学者对其进行了研究[4-13],包括初始值确定[4-5]和背景值构造两方面[6-13].初始值确定虽然在一定程度上影响了GM(1,1)模型的预测精度,但是最主要的精度影响因素还是背景值构造的缺陷.文献[7-8]以拉格朗日中值定理在理论上分析了背景值构造的不足,文献[9]从几何思想上分析了背景值构造的不足,文献[10-12]从积分思想上分析了背景值构造的不足,文献[13]在非严格等比数列的基础上对积分思想的背景值构造进行进一步优化.本文将基于文献[13]提出的非严格等比数列(文中称之为近似指数序列)思想,重新审视文献[12]中的背景值构造,并指出文献[13]优化方法的不足,建立新的背景值构造形式.实例应用结果显示,新背景值构造形式下的GM(1,1)模型具有更高的精度.

1 GM(1,1)模型建模机理及其缺陷

令x(0)为GM(1,1)建模序列

令x(1)为x(0)的AGO 序列

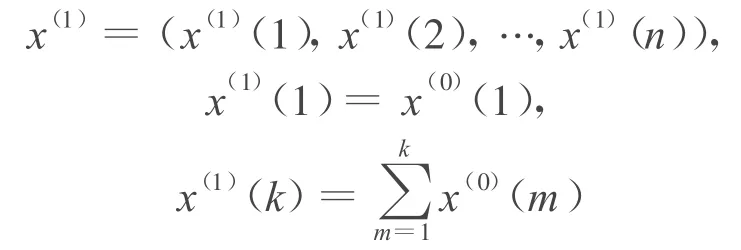
令z(1)为x(1)的均值(MEAN)序列

则GM(1,1)的定义型,即GM(1,1)的灰微分方程模型为

式中,a为发展系数,b为灰作用量,是微分方程的参数.

灰微分方程白化型为

GM(1,1)白化型响应式为

由最小二乘法,可以求得参数

在区间[k-1k]上对灰微分方程白化型两边积分[12]:

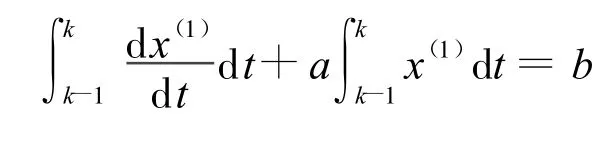
即

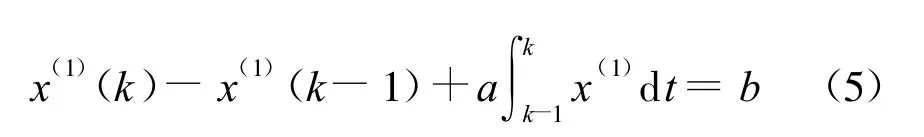
将式(5)与灰微分方程x(0)(k)+az(1)(k)=b比较可以得到两者的差别仅为x(1)(k-1)),显然以x(1)(k-1))更能适应灰微分方程白化型.文献[12]以原始数据为纯指数序列的前提下导出的表达式,具体如下:

假设原始数据x(0)(k)=gea(k-1)为纯指数序列,则其一次累加序列为x(1)(k)=Gea(k-1)+C,其中G=g(1-e-a)-1,C=-Ge-a,k=1,2,…,n.

经计算可得

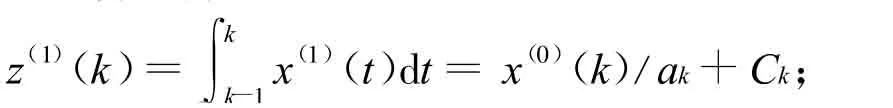
2 背景值构造的重新优化

文献[13]指出文献[12]中的背景值构造是基于纯指数序列推导出的,其并不适合于非严格等比序列或者说近似指数序列,并给出了优化后的背景值形式

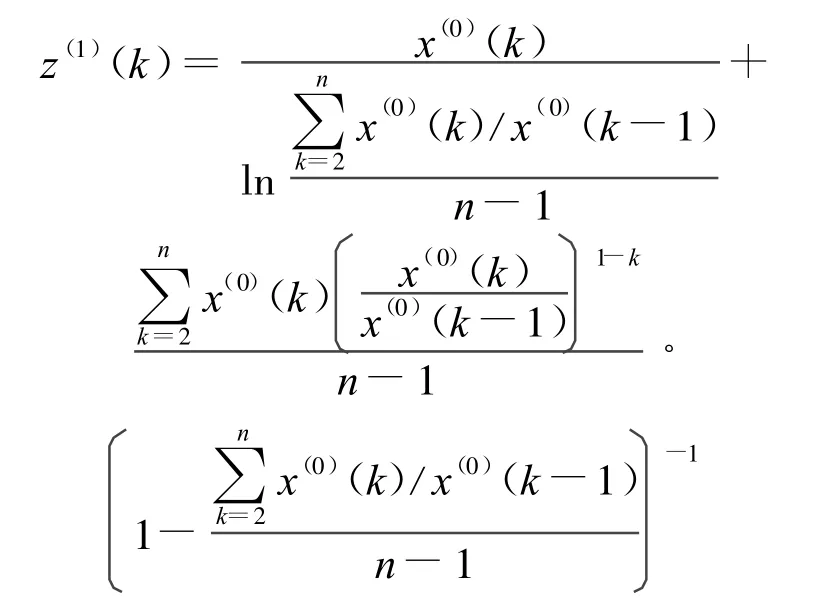
文献[13]虽然认识到了由纯指数推导出的背景值构造形式并不适合于近似指数序列,但是其仅仅是将文献[12]中的ak和Ck用近似值a′和C来代替,该方法并不能从根本上解决背景值构造形式对近似指数序列的适用性问题.下面仍以文献[12]中的积分思想推导出新的背景值构造形式.

至于动态修正项的求解本文采用具有全局寻优能力的遗传算法.具体操作可利用Matlab编程及其遗传算法工具箱,在原始数据残差平方和最小目标下进行搜寻,即

3 实例分析

以江苏省1997～2002年的财政科技投入数据[12]建立原GM(1,1)模型、文献[12-13]中背景值重构模型以及本文模型,原始数据见表1,各模型预测值见表2.

表1 1997～2002年江苏省财政科技投入

表2 各模型预测结果比较

利用1997～2002年的财政科技投入数据建立原GM(1,1)模型得时间响应式为

建立文献[12]中背景值重构模型时间响应式为

建立文献[13]中再优化模型,得时间响应式为

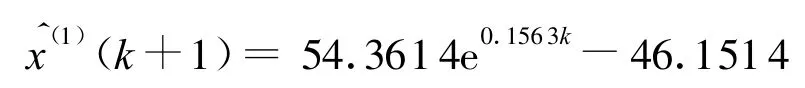
建立本文重新优化模型,得时间响应式为

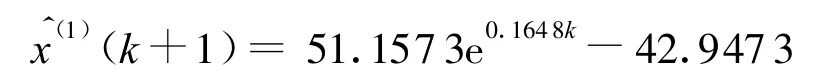
其中 α(k)={-0.204,0.350,0.031,4,0},k=2,3,4,5,6,它们的累加还原值为

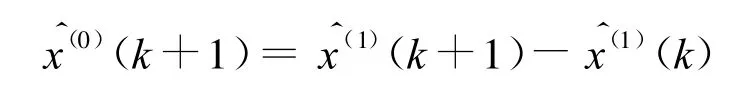
从表2预测结果可以看出由纯指数导出背景值形式的文献[12]中的改进模型以及将级比看作常数的文献[13]中再优化模型都不适合于近似指数序列,文献[12]模型预测值明显偏大,而文献[13]模型预测值明显偏小,两种模型预测精度甚至不如原始的GM(1,1)模型,这样的改进意义不大,而本文的重新优化模型解决了GM(1,1)模型对于近似指数序列拟合的问题,其残差平方和由GM(1,1)模型的0.294减小到了0.279,提高了预测精度.