噪声关联程度时间周期调制频率对单模激光随机共振的影响

闫旭东

(湖北工业大学理学院,武汉 430068)

随机共振概念提出30年来,随机共振现象多次被实验所观察,对随机共振现象的研究成为人们关注的重要课题,并有大量的理论和实验研究报道[1-7].采用线性化近似理论讨论随机共振已有很多研究成果[8-11],陈德彝等对噪声关联程度受时间周期调制情况下的随机共振进行了系列讨论[12-17].在“噪声关联程度的时间周期调制对单模激光随机共振的影响”一文[17]中指出,输出信噪比R随抽运噪声强度Q的变化曲线,以及输出信噪比R随量子噪声强度D的变化曲线,都存在随机共振,并且都随噪声关联程度时间周期调制的频率 Ωλ而变化.当 Ωλ增大时,共振峰向左移,且振幅降低,最后共振消失.我们进一步仔细研究了噪声关联程度时间周期调制的频率 Ωλ的变化对R-Q曲线和R-D曲线的影响,发现一新的现象:随着噪声关联程度时间周期调制的频率 Ωλ的变化,R-Q曲线和R-D曲线都会反复出现由共振到单调衰减的变化.

1 噪声关联时间周期调制下的单模激光的信噪比

受信号调制的单模激光增益模型的光强朗之万方程是:

式中,Ωλ是对噪声间关联程度λ的时间周期调制频率,I表示光强,K为损失系数,Γ是增益系数,β=A/Γ,式中,A为自饱和系数,D是量子噪声强度,A为输入信号振幅,Ω为输入信号频率.

方程(1)中噪声ξ(t)和 η(t)的统计性质为

式中,Q是抽运噪声强度,λ为噪声间关联程度.

平均光强相关函数为

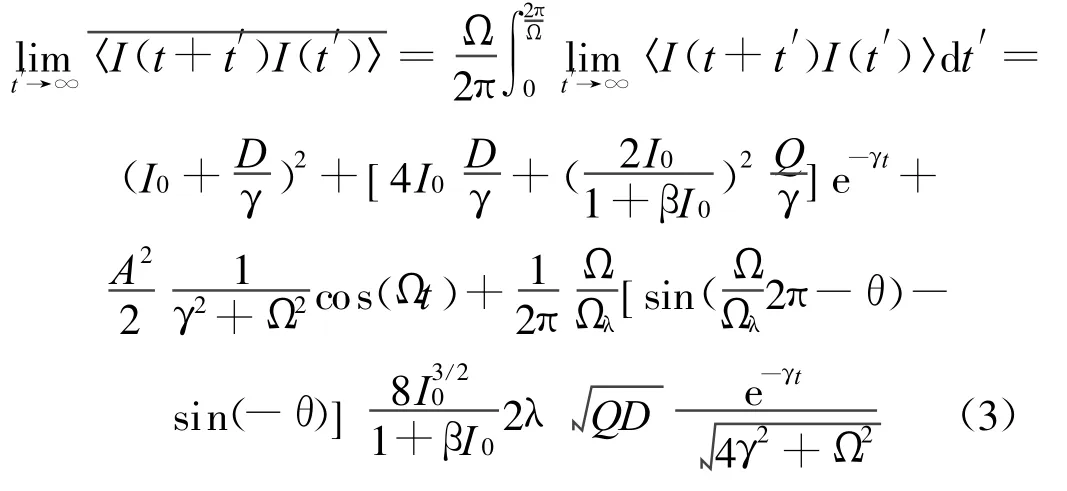
输出功率谱为

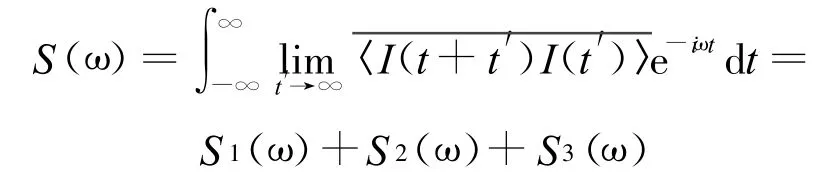
其中:

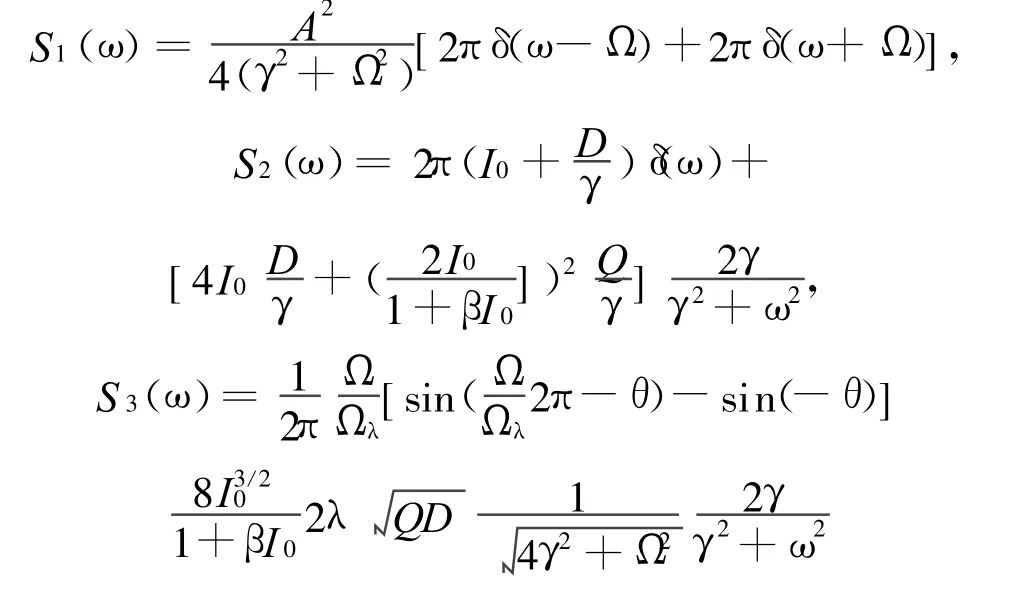
式中,S1(ω)是输出信号功率谱,S2(ω)和S3(ω)是输出噪声功率谱.

输出信号总功率为

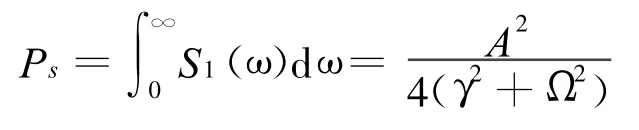
ω=Ω处单位噪声谱的平均功率是

最后计算出输出信噪比:

表达式中θ由下式确定:

当 Ω=nΩλ(n=1,2,3,…)时,输出信噪比为

即输入信号频率为时间周期调制频率的整数倍时,输出信噪比与噪声间关联程度λ无关.

本文以下仅讨论 Ω≠nΩλ(n=1,2,3,…)时的情况.

2 讨 论

2.1 R-Q曲线随噪声关联时间周期调制频率 Ωλ的变化

图1和图2都是输出信噪比R随抽运噪声强度Q在不同调制频率Ωλ下的变化曲线.

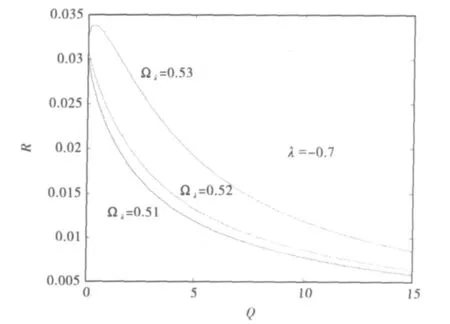
图1 Ωλ由0.53到 0.51时R-Q曲线的变化

图 2 Ωλ由0.45到0.43时 R-Q曲线的变化

图1显示,当噪声关联时间周期调制频率 Ωλ的值由0.53变化到0.51时,R-Q曲线经历了由共振到单调衰减的变化;图2表明,当噪声关联时间周期调制频率Ωλ的值由0.45变化到0.43时,R-Q曲线再次经历了由共振到单调衰减的变化.研究表明,随着噪声关联时间周期调制频率Ωλ的变化,这种由共振到单调衰减的变化会重复发生.

2.2 R-D曲线随噪声关联时间周期调制频率 Ωλ的变化

图3和图4都是输出信噪比R随抽运噪声强度D在不同调制频率Ωλ下的变化曲线R-D曲线,它们和R-Q曲线表现出相同的特性.图3中,当噪声关联时间周期调制频率 Ωλ的值由0.81变化到0.79时,R-D曲线经历了由共振到单调衰减的变化;图4中,当噪声关联时间周期调制频率 Ωλ的值由1.1变化到1.08时,R-D曲线再次经历了由共振到单调衰减的变化.研究也表明,随着噪声关联时间周期调制频率Ωλ的变化,这种R-D曲线由共振到单调衰减的变化也会重复发生.

图3 Ωλ由0.81到0.79时 R-D曲线的变化

图4 Ωλ由1.1到1.08时 R-D曲线的变化

3 结 论

研究证实了文献[17]中关于 Ωλ的变化导致RQ和R-D曲线共振峰消失的结论,并且进一步发现:R-Q和R-D曲线会随着噪声关联时间周期调制频率Ωλ的变化周期性地出现由共振到单调衰减的变化.这一发现提示,在一定程度内,可利用噪声间关联程度系数λ的时间周期调制频率Ωλ来控制激光光强.

[1]Benzi R,Sutera A,Vulpiani A.The Mechanism of Stochastic Resonance[J].J.Phys.A.Math.Gen.,1981,14(11):453-457.

[2]Gammaltoni L,Haggi P,Jung P,et al.Stochastic Resonance[J].Rev.Mod.Phys.,1998,70(1):223-287.

[3]胡 岗.随机力与非线性系统[M].上海:上海科技教育出版社,1994.

[4]McNamara B,Wiesenfeld K.Theory of Stochastic Resonance[J].Phys.Rev.A.,1989,39:4854-4868.

[5]Hu G,Nicolis G,Nicolis C.Periodically Forced Fokker-Planck Equation and StochasticResonanceVPhys[J].Rev.A.,1990,42:2030-2041.

[6]Hu G,Haken H,Ning C Z.A Study of Stochastic Resonance without Adiabatic Approximation[J].Phys.Lett.A.,1992,172:21-28.

[7]张良英,曹 力,吴大进.具有色关联的色噪声驱动下单模激光线性模型的随机共振[J].物理学报,2003,52:1174-1178.

[8]韩立波,曹 力,吴大进等.信号直接调制下色关联噪声驱动的单模激光的随机共振[J].物理学报,2004,53:2127-2132.

[9]张良英,曹 力.[J].华中科技大学学报:自然科学版,2005,33(8):119-120.

[10]程庆华,曹 力,吴大进.信号调制色泵噪声和实虚部间关联量子噪声驱动下单模激光的随机共振现象[J].物理学报,2004,53:2556-2562.

[11]韩立波,曹 力,吴大进等.偏置信号调制下色关联噪声驱动的单模激光的光强相对涨落[J].物理学报,2004,53:3363-3368.

[12] Chen Deyi,Zhang Li.Stochastic resonance driven by time-modulated correlated coloured noise sources in a single-mode laser[J].Chinese Physics B,2009,18(5):1755-1760.

[13]陈德彝,王忠龙.偏置信号调制下噪声关联的周期调制对单模激光随机共振的影响[J].物理学报,2009,58:2907-2913.

[14]陈德彝,王忠龙.信号调制下色噪声间关联的周期调制对单模激光随机共振的影响[J].物理学报,2009,58:1403-1409.

[15]陈德彝,王忠龙.噪声交叉关联程度受时间周期调制下单模激光的光强关联时间[J].中国激光,2009,36(1):119-124.

[16]陈德彝,王忠龙.色噪声间关联的周期调制对单模激光随机共振的影响[J].物理学报,2009,58:102-106.

[17]陈德彝,王忠龙.噪声间关联程度的时间周期调制对单模激光随机共振的影响[J].物理学报,2008,57(6):3333-3336.