三峡水库中期优化调度方法研究

董晓华 刘 冀 邓 霞 薄会娟

(三峡大学土木水电学院,湖北宜昌 443002)

三峡水电站是当今世界单机容量和总装机容量最大的水电站.三峡水电站单机容量70万kW,一台机组的出力足以满足一个拥有100万人口的城市的用电需求.在兼顾其他兴利要求的前提下,采取措施优化发电调度方法,将带来巨大的发电效益.

三峡工程建成后,将暂时以调度图调度,并辅以一些调度规则[1].调度图由一些控制水库蓄供水的指示线所划分的不同电站出力区组成.依据调度图进行调度所需的输入和输出之间的关系可以表达为下列函数关系

式中,N为电站平均出力(MW);H为库水位(m);t为水库当前所处的时段(d).

利用调度图对水库进行调度的优点在于两点:(1)偏于安全;(2)日常调度中便于实施.这也是目前国内的大部分水库的调度方法仍然采用调度图的原因.

但是,如果将一个水库看做一个物理系统,系统输入将为入库径流,系统输出将为发电流量(或出力),系统的状态变量将为库水位和时间.由公式(1)可见,应用调度图进行水库调度时,只考虑了某时段t的系统输出N,和状态变量H,而没有考虑时段t的系统输入:入库径流量I.在缺少系统输入信息的情况下,调度图的调度方式将很难对面临时段的发电量作出优化,以获得最大发电量,因此有必要采用优化方法改进对水库的调度.优化调度法依据所采用的算法,可分为线性规划[2],非线性规划[3],动态规划[4-6],遗传算法[7],多目标优化[8-9]及大系统协调分解法[10],蚁群算法[11],混沌算法[12].其中,动态规划法理论较为完善,应用最广泛,因此文章将以动态规划法为优化算法,研究三峡水库的中长期优化调度方法,以及它们之间的耦合方法;然后应用所开发的优化模型,模拟中期(3～7 d)入库径流的预见期对发电调度结果的影响,以验证该模型的合理性.

1 优化算法-离散动态规划法

1.1 原理

在研究中将使用离散动态规划法(Discretized Dynamic Programming,DDP)对三峡水库的调度进行优化.

离散动态规划法的结构是由时段、状态变量、决策变量、目标函数、约束以及递归方程组成的.在一个调度周期内,重复针对每一个时段应用递归方程,就可以获得最优调度策略.在研究中,1994水文年(从1994年6月1日至1995年5月31日)的数据被用来应用研究所开发的方法.

研究针对三峡工程完建后的工程状态,根据设计和调度规程,三峡水库以防洪为主,发电服从于防洪.为了防洪需要,每个水文年的供水期末,库水位应降至防洪限制水位,即每年5月末至6月上旬,水库库水位逐步降至145m,6月中旬至9月底水库一般维持在防洪限制水位145m运行.汛后10月份,水库蓄水,库水位逐步升高至正常蓄水位175m运行.研究以汛初为优化调度的起始点,则初始状态应为145 m,调度周期末的终止状态也应为145m.

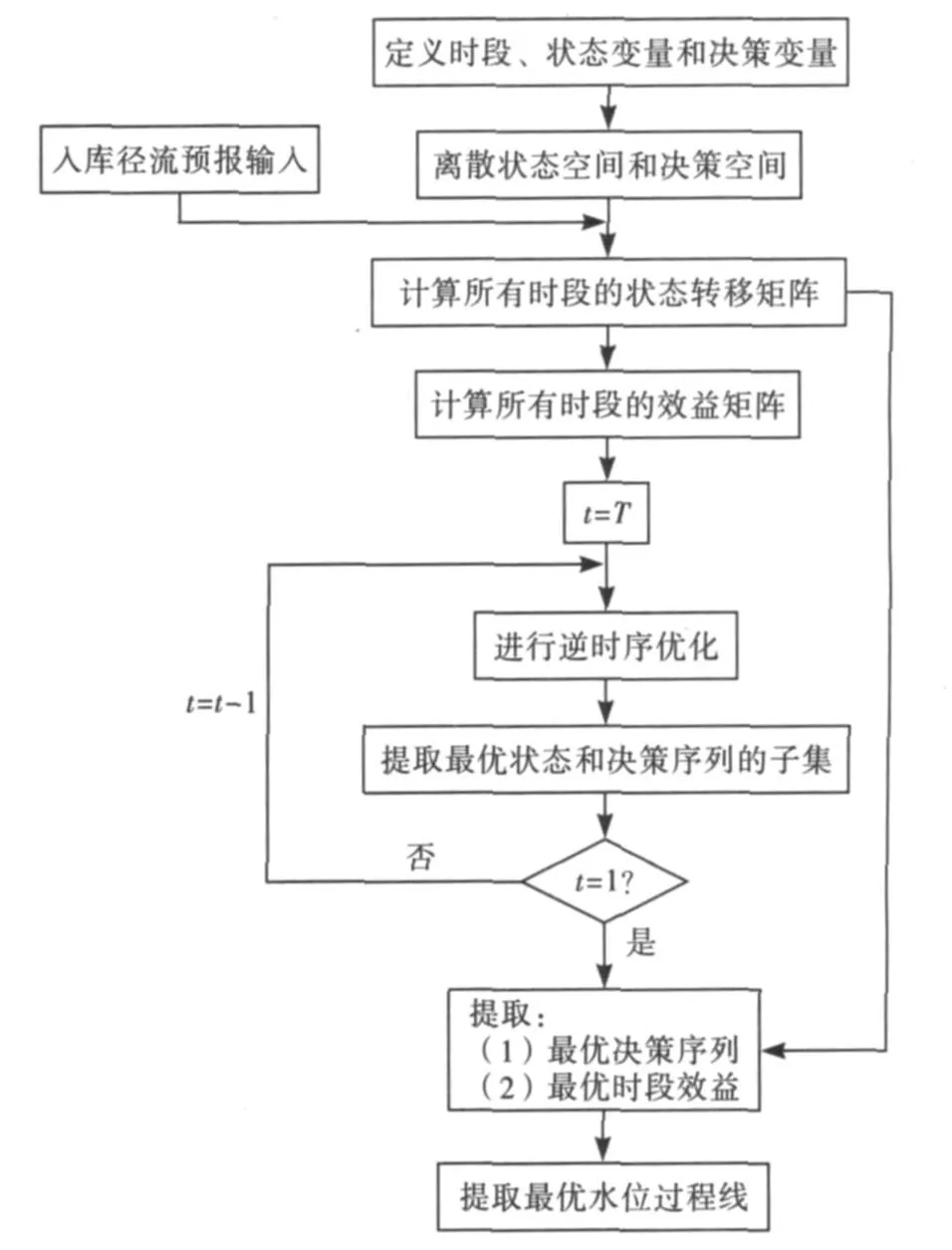
图1 离散动态规划法(DDP)算法的计算框图

图1给出了算法的计算流程.DDP算法使用状态转移方程,根据面临时段的入库流量和水库蓄水量计算下一时段的水库蓄水量,即

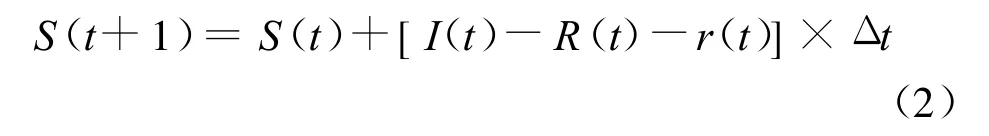
式中,R(t)为t时段三峡水库的发电流量(m3/s);r(t)为t时段三峡水电站的弃水流量(m3/s);S(t)为t时段三峡水库的库水量(m3);I(t)为t时段三峡水库的入库流量(m3/s);Δ(t)为时段长(月或d).

传统的DDP算法中,使用大量的循环语句来计算在特定时段、特定状态(库水位)、特定决策(出库流量)下,下一个时段的出库流量和时段末的水库蓄水量,这是造成DDP算法速度慢和占用大量内存的主要原因.

为提高DDP的效率,研究将每一个时段的状态转移数值预先计算出来,存储为一个2维矩阵,称为状态转移矩阵;一个优化循环内所有时段的2维状态转移矩阵将被组合在一起,构成一个3维的状态转移矩阵.在应用DDP的逆(或顺)时序递推算法寻求每个时段的最优调度方案时,就只需要从此3维状态转移矩阵中查出下一阶段的库水位(或水库蓄水量)即可,省去了循环计算公式(2)的时间.

1.2 目标函数和约束

三峡水库调度的目标是:在满足防洪要求的前提下,综合考虑上、下游的航运和排沙要求,使电站获得最大的发电效益.

根据此目标,三峡水库优化调度的目标函数可以写为

约束条件为:

(1)水量平衡:与公式(2)相同.

(2)状态变量变化约束范围:即各时段的库水位不低于死水位,也不能超过该时段允许的最高蓄水位

(3)电站出力限制条件

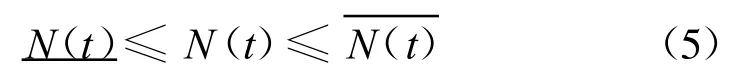
(4)电站水量限制条件

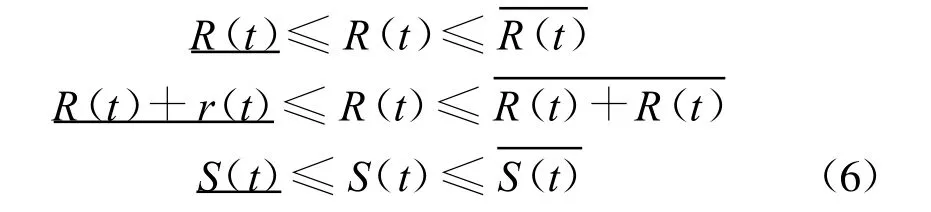
式中,B为三峡总发电量(kW◦h);Tl为入库径流预报的预见期(月或d);g为重力加速度,9.81m/s2;η为三峡水电站的机组效率,取 η=0.85;H1(t)为t时段三峡水库的库水位(m);H2(t)为t时段三峡水库的尾水位(m )为t时段三峡水库的库水位上限(m),175m ;为t时段三峡水库的库水位下限(m),145m;R(t)为t时段三峡水电站的发电流量(m3/s);r(t)为t时段三峡水电站的弃水流量(m3/s);S(t)为t时段三峡水库的库水量(m3);I(t)为t时段三峡水库的入库流量(m3/s);Δt为时段长(月或d);N(t)为t时段水电站的出力(kW)为t时段水电站的出力下限(kW)为t时段水电站的出力上限(kW)为t时段水电站的的发电流量下限(m3/s),为 700m3/s为t时段水电站的的发电流量上限(m3/s),为26×9.66 m3/s为t时段水电站的的发电流量加弃水量的下限(m3/s),为6000 m3/s ;为t时段水电站的的发电流量加弃水量的上限(m3/s),为54 000m3/s;S(t)为t时段水库的蓄水量下限(m3),根据死水位从库水位-蓄水量曲线查得;为t时段水库的蓄水量上限(m3),根据正常蓄水位从库水位-蓄水量曲线查得.

1.3 解目标函数的回归方程

研究使用逆时序递归算法来寻找最优调度策略和最优状态.递归方程是

式中,Bt(Ht,It,Rt)是时段t至最后时段T的最优子调度策略;bt(Ht,It,Rt)是时段t的阶段发电效益(kW◦h);Bt+1(Ht+1,It+1,Rt+1)是时段t+1至最后时段T的最优子调度策略;BT+1(HT+1,IT+1,RT+1)是边界条件,此处假设终止时段之后的时段的阶段效益为0;Ht是t时段三峡水库的发电水头(m),Ht=H1(t)-H2(t);It是t时段三峡水库的入库流量(m3/s);Rt是t时段三峡水电站的发电流量(m3/s).

这一递归方程最开始从最后一个时段应用,逆时序向前直到第一个时段.随后,正时序地从头至末应用状态转移方程,从而计算出最优状态轨迹(库水位变化过程)和最优效益.

2 满足保证出力要求的方法

对三峡水库的发电调度的一个要求是在96%的设计保证率下,输出4990MW的保证出力.为实现这一调度目标,拟对目标函数,即公式(3)中增加一项惩罚函数,则式(3)变为

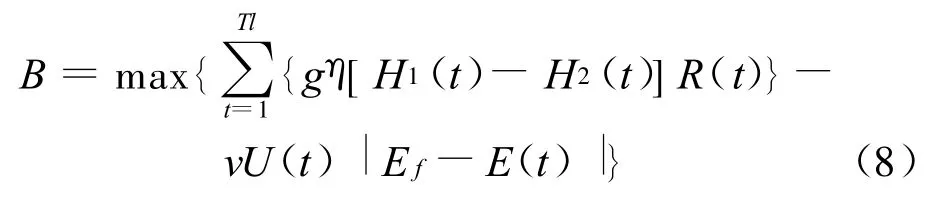
式中,v为当时段平均出力低于保证出力时的惩罚因子;U(t)为单位阶跃函数为保证电能,Ef=NfΔt;E(t)为t时段电站的发电量(kW◦h);Nf为三峡电站的保证出力,为4990MW.

为使三峡电站在相应的保证率下输出保证出力,需要正确确定惩罚因子v的数值.确定的方法是使用历史入库径流数据对三峡水库进行模拟调度,获得v与保证率之间的关系,其中产生设计保证率的v值即为所寻求的惩罚因子.通过此方法确定的惩罚因子v的值为0.4.

3 长期和中期优化调度模型的耦合

对水电站的优化调度可以通过平衡当前和将来时段的发电效益来实现,即需要权衡在何时消耗有限的存水发电来获得最大发电量.对当前一个阶段的优化必须在长期优化结果的指导下进行.因此,需要有一种时间分解的机制来将长期优化调度的结果传递给中期优化调度模型.传递过程中,必须明确长期和中期优化模型之间的关系.

研究使用如图2所示的原理来实现长期和中期优化调度模型的耦合.

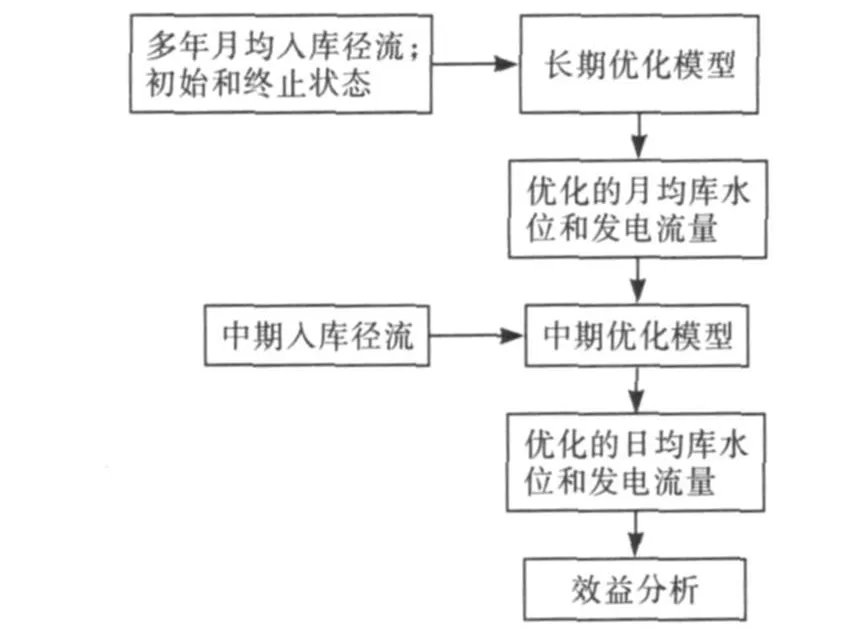
图2 长期和中期优化调度模型耦合的分层结构

在图2中,对三峡水库的优化调度分2步进行:(1)以月为时段的长期优化;(2)以天为时段的中期优化.长期优化的目的是优化水库的月均泄水,并提出每月优化的月末水位.为实现此长期优化,将使用从历史数据中获得的月均入库流量作为长期优化的输入.长期优化模型所产生的优化的月水位和月均泄水将被内插成日均库水位.日均库水位将被用于中期优化调度模型的引导准则,用于指导中期优化.中期优化模型将以中期入库径流预报为基础,并在长期优化结果的指导下,优化日均水库泄流.所产生的日均泄流和库水位将被用来进行日常水库调度,在研究中也将被用来计算优化模型的效益.

4 结 果

具有不同质量的入库径流预报结果输入优化模型后,输出的发电效益肯定不同,为比较不同质量的预报对发电效益的影响,需要确定一个比较的基准.传统的基准是往年的实际发电量.使用这个基准的缺陷有:(1)各年的发电效益实际上主要取决于水情,每年的水情不同,发电量必然不同,如果以丰水年的发电量去比较枯水年的发电量,显然不妥;(2)每年的水库调度策略带有强烈的随机性、主观性和政策性.通常必须从更广的范围内,由电网乃至国电公司和国家防总综合调度,因此很难客观判定水库调度者在某一年的调度策略的质量.

为解决这一问题,在此引入“理论年最大发电量”作为不同预报质量(乃至不同调度策略)所产生的发电效益的优劣的判据.

理论年最大发电量是假设已知全年的入库流量,通过优化程序计算得到的年最大可能发电效益.在此情况下也不考虑汛限水位.如果以入库流量的不确定性为唯一的不确定因素源,不考虑其它的不确定性源(如水库的机械故障,误操作等),则此发电效益应该是理论上可能获得的最大发电量,对于特定年是唯一的,适于用作比较的标准.根据计算结果,1994年的理论年最大发电量是8.8477×1010kW◦h.

利用上述优化调度模型,对1994水文年度三峡水库的发电调度进行了模拟.此处入库径流预报的预见期为3～7d,预报误差假设为0.调度结果见图3,预报误差为零的不同预见期下的发电量见图4.

从图3～4中可以看到,预见期越长,能够获得更高的库水位,相应的发电量也越高.在7 d的预见期下,如果预报误差为0,则年平均发电量(7.51×1010kW◦h)可达理论年最大发电量(8.847 7×1010kW◦h)的85%.同时,从图3(b)可见,中期优化模型能很好地跟随长期优化结果,证明研究所提出的耦合方法是有效的.

5 结 论

以三峡水库为研究对象,开发一个基于入库径流预报的,长中期优化模型耦合的水库调度模型;然后利用这一模型,研究了入库径流预报的预见期年发电量的影响.

应用此耦合模型进行三峡水库调度模拟的结果显示,这种耦合机制的设计是成功的.长期优化的库水位轨迹能很好地指导中期优化调度.对于预见期与年发电量的关系,发现在7d以内,入库径流预报的预见期越长,所获得的年发电量越大.在7 d的预见期下,年发电量最大可达理论年最大发电量(8.85×1010kW◦h)的85%.

[1]长江水利委员会.三峡工程综合利用与水库调度研究[M].武汉:湖北科学技术出版社,1997.

[2]Needham J,Watkins J.Linear Programming for Flood Control in the Lowa and Des Moines Rivers[J].Journal of Water Resources Planning and Management,2000,126(3):118-127.

[3]吴保生,陈惠源.多库防洪系统优化调度的一种算法[J].水利学报,1991,11:35-40.

[4]Bellman R,Drefus S.Applied Dynamic Programming[M].Priceton,N.J.:Pricetion University Press,1962.

[5]Bellman R.Dynamic Programming[M].Priceton,N.J.:Princeton University Press,1957.

[6]徐 慧,欣金彪,徐时进.淮河流域大型水库联合优化调度的动态规划模型解[J].水文,2000,20(1):22-25.

[7]钟登华,熊开智,成立芹.遗传算法的改进及其在水库优化调度中的应用[J].中国工程科学,2003,5(9):22-26.

[8]贺北方,丁大发,马细霞.多库多目标最优控制运用的模型和方法[J].水利学报,1995,3:84-88.

[9]梁业国,魏 莉.水电站水库洪水调度的多目标模糊决策[J].三峡大学学报:自然科学版,2001,23(6):556-559.

[10]黄志中,周之豪.水库群防洪调度的大系统多目标决策模型研究[J].水电能源科学,1994,12(4):237-245.

[11]马 良.基于蚂蚁算法的函数优化[J].控制与决策,2002,11:719-726.

[12]邱 林,田景环,段春青等.混沌算法在水库优化调度中的应用[J].中国农村水利水电,2005(7):1007-2284.