一种ECC快速签名在电子政务中的应用

李成霞 徐守志 周 欢

(三峡大学电气信息学院,湖北宜昌 443002)

随着网络技术的发展以及政府推进电子政务力度的加强,无纸化办公已经成为政府及各企业发展的一种趋势,但是电子公文涉及到各党政机关的机密信息,因此安全问题非常重要,只有解决好安全问题才能推动电子政务向前发展.安全问题主要涉及到电子公文的安全传输和身份认证问题.签名技术是密码学的核心技术之一,可以保证信息在网络传输过程中的完整性和不可否认性.椭圆曲线密码体制[1-2]是Neal Koblitz和VS Miller在1985年提出来的,它可以用较小的密钥获得较高的安全性,与已有的公钥体制相比(比如RSA)具有安全性高、计算量小、处理速度快、存储空间占用小的优点.因此将基于椭圆曲线的数字签名用于解决电子公文的安全性问题具有广泛的应用前景.本文主要运用非相邻二进制法和变长滑动窗口相结合的方法提高椭圆曲线密码体制中的点乘运算效率,能在更长的密钥长度下保证签名的速度,并将其用于电子公文在传输过程中对机密信息的签名,保证了安全性的同时也提高了签名速度.

1 椭圆曲线密码体制

1.1 ECDSA参数

ECDSA全局参数表示为(q,a,b,G,n,h),其中q为有限域的大小,本文探讨素数域上的ECC,选择方程y2=x3-3x+bmodq,GF(q)表示一个有限域,a,b∈GF(q)为椭圆曲线E的参数,基点G=(xG,yG),的阶为素数=#E(GF(q))/n.

用户私钥为随机整数d∈[1,n-1],相应的公钥为Q=dG.

1.2 椭圆曲线数字签名方案

发送端完成对信息m的签名,签名为(r,s):

(1)对于待签名信息m,用哈希函数SHA-1,计算e=H(m),并转化为一个160位的整数;

(2)任意选取一个随机整数k,k∈[1,n-1],计算kG=(x1,y1);

(3)计算r=x1modn,如果r=0,则返回(2)重新选择k;

(4)计算s=k-1(e+dr)modn,如果s=0,则返回(2);

接收端验证签名(r,s)是否是发送端对消息m的签名:

(1)判断(r,s)(r,s)是否属于[1,n-1],否则签名无效;

(2)计算e=H(m);计算w=s-1modn;计算u1=ewmodn,u2=rwmodn;

(3)计算X=u1G+u2Q,如果X=O表示签名无效;否则X=(x1,y1)计算v=x1modn;

(4)若v=r,则签名有效;否则无效.

1.3 基于可变窗口机制ECC快速签名算法

从椭圆曲线签名、验证方案可知,共需要4次点乘运算,点乘算法是影响执行效率的重要因素之一,因此如何提高点乘算法的运算速度是提高整个ECC签名的关键之一.

1.3.1 点乘算法

在给定的有限域上,一个椭圆曲线上的点P和一个随机大整数K相乘被称为点乘,也是P自身相加K次.KP运算速度取决于整数K的二进制长度的缩短,或非零个数的减少.点加由非零个数决定,倍点是由二进制位数决定的.一般一个确定的二进制位数无法改变,所以倍点运算次数无法改变,NAF、滑动窗口法等主要是通过减少点加来提高运算速度的.NAF法较“平方-乘”方法大约快1/8,在滑动窗口算法中变长滑动窗口较占优势[3].NAF表示法具有最少的非零元素,而变长滑动窗口法可以灵活地改变窗口大小,所以采用NAF和变长滑动窗口相结合的方法实现点乘算法来提高速度.一个正整数K的非相邻表达式为NAF(K)计算参考文献[4].

在NAF法与变长滑动窗口法相结合中,可以将NAF(K)中的元素划分为零窗口和非零窗口,例如可以计算出NAF(1031)={1,0,0,0,0,0,0,1,0,0,-1},观察窗口中的元素:含有6个和2个连续的零,所以分别将其划为零窗口,因此窗口最后划分为E4、E3、E2、E1、E0,其中E4 窗口元素为{1},长度为 1;E3窗口为{0,0,0,0,0,0},长度为6;E2窗口元素为{1},长度为1;E1窗口元素为{0,0},窗口长度为2;E0窗口元素为{-1},长度为1.结合NAF法和变长滑动窗口法,本文所设计的点乘算法流程图如图1所示.可以计算出1031P=210P+23P-P=21(22(21(26P+0P)+1P)+0P)+(-1)P,所以点乘KP的计算公式可以表示为是第i个窗口,l(Ei)是第i个窗口的长度.

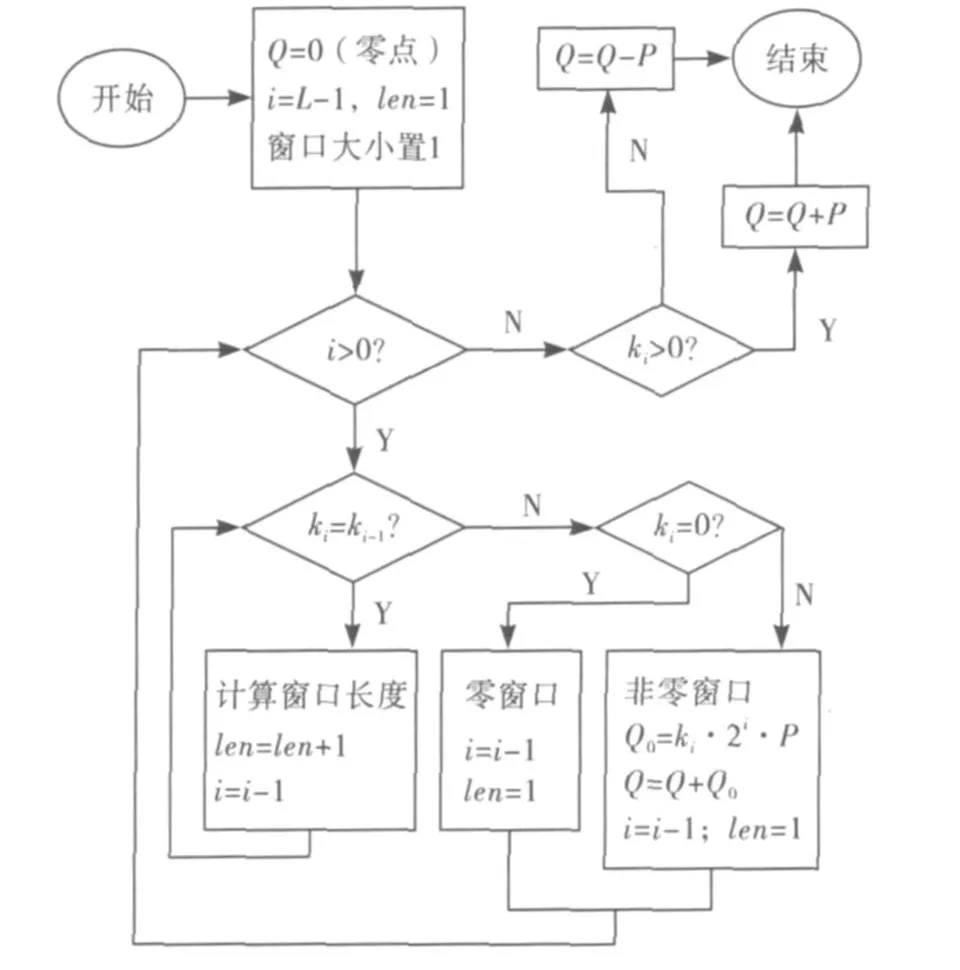
图1 点乘算法流程图

因为NAF(K)中没有两个连续的非零元素,所以在窗口划分为零窗口和非零窗口时,只可能是{1}、{-1}、{0,0,…0}这3种情形的窗口,所以图2非零窗口的计算式Q0=ki◦2i◦P中的ki只能为±1,因此在整个计算中最费时的是Q0=2iP.所以在进行该点乘算法时,先分析NAF(K)中非零元素的位置并进行适当预计算(2iP),在综合时间和空间条件下,提高整个点乘算法的运算速度.

1.3.2 点加和倍点

点乘可以分解为倍点和点加运算,在点加和倍点的计算中主要考虑避免求逆,因为在Fq域上的求逆操作相当慢,大概相当于80多次乘法操作.各坐标中点加和倍点计算[5]所需域操作个数如表1:求逆(I),平方(S),乘法(M).由表1可知,雅可比投射坐标下倍点速度最快,且利用所选取的椭圆曲线方程(y2=x3-3x+bmodq)时,倍点速度可以达到 4M+4S,雅可比-仿射坐标下点加速度最快.在点乘中,Q始终以雅可比投射坐标系(X∶Y∶Z)形式表示,Q0以仿射坐标(x,y)表示,Q=Q+Q0中,输入以雅可比投射坐标表示的Q和仿射坐标表示的Q0,调用雅可比-仿射的点加算法[5]得到以雅可比投射坐标表示的点加结果Q=kp=(X∶Y∶Z),最后再转化为仿射坐标表示(XZ-2,XZ-3).

表1 各坐标下点加和倍点所需域操作数

2 ECC快速数字签名技术在电子政务中的应用

公文涉及到各党政机关及企业内部机密信息,所以公文在网上传输时安全问题变得特别重要.数字签名是主要的密码技术之一,数字签名使得信息的接收者能够验证信息来源的真实性、验证信息是否完整,还提供了不可抵赖性,该特性能够保证信息的发送者无法否认自己确实发送了这个信息,公文的传输采用数字签名技术能够保证公文在传输过程中不被违法者截取、任意修改、删除、以及不被违法者冒充生成并发送.

例如:公文发送者A和公务接收者B之间完成一种公文签名及传输的流程如图2所示.

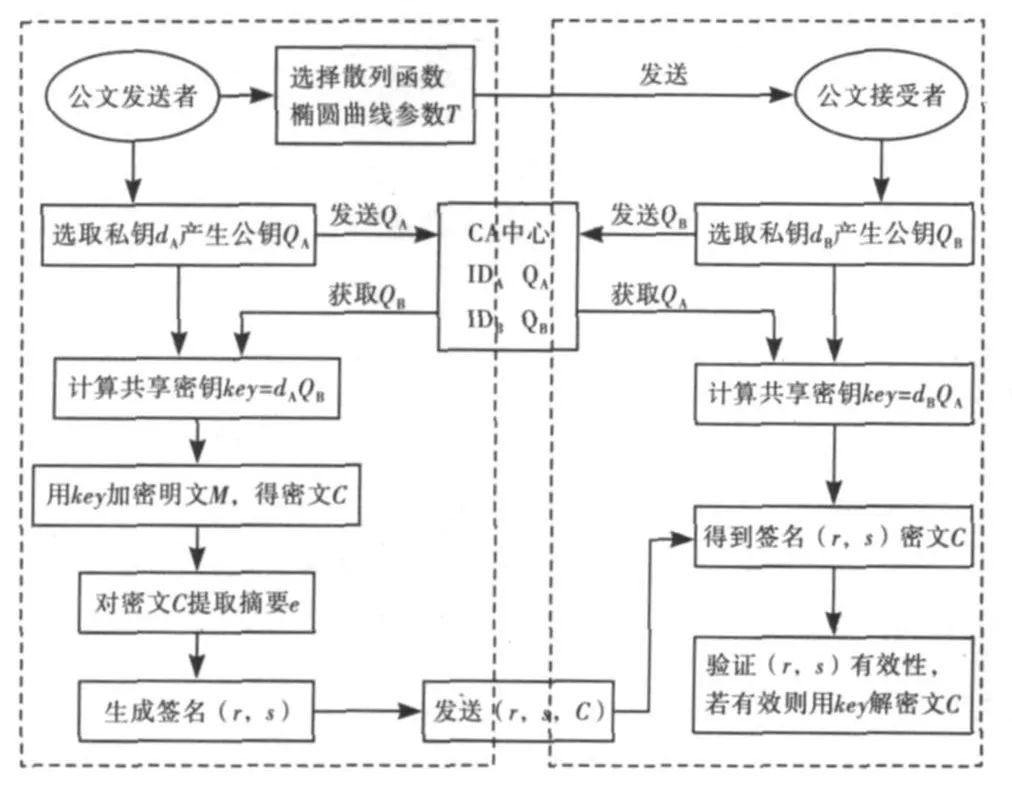
图2 公文签名和传输过程

公文发送者A的过程:

(1)A要选取散列函数SHA-1和椭圆曲线参数T=(q,a,b,G,n,b)发给接收者;

(2)A根据T产生自己的私钥dA,计算公钥QA=dAG,并分别将公钥发给CA;

(3)A从CA那获取B的公钥QB,计算共享密钥key=dAQB;

(4)用共享密钥加密A所需要发给B的公文M,得出密文C,e=S HA-1(C);

(5)A选择一个随机数k,k∈[1,n-1];

(7)计算s=k-1(e+dAr)modn,若s=0,返回(5);

(8)将(r,s,C)发给B.

公文接受者B的过程:

(1)从A那获得散列函数SHA-1和椭圆曲线参数T=(q,a,b,G,n,b);

(2)利用椭圆曲线参数生成自己私钥dB,计算公钥QB=dBG,并将公钥发给CA中心;

(3)从CA中心获取A的公钥QA,计算共享密钥key=dBQA,因为key=dAQB=dBQA;

(4)对A发过来的(r,s,C),分解得签名(r,s)和密文C;

(5)验证s,r是否为(1,n-1)间的整数,若是,则继续,否则无效;

(6)B利用散列函数对C产生摘要e=SHA-1(C);

(7)计算w=s-1modn;计算u1=ewmodn,u2=rwmodn;

(8)利用A的公钥QA计算X=u1G+u2QA,如果X=O表示签名无效;否则X=(x1,y1)计算v=x1modn;

(9)若r=v,则接受该签名,用共享密钥key解密C,得M.

整个过程可以保证在公文传输过程中,满足了信息安全的所有目标.身份认证性:签名时,使用私钥加密,公钥解密,就可以确认消息是否由私钥的所有者发出;数据完整性:生成签名(r,s),然后将(r,s,C)作为一个混合的整体数据发给接受方,不可能篡改,从而保证了数据的完整性,保证了内容不被篡改;不可否认性:发送者不可能事后否认他发送过的信息,信息的接受方可以向CA证实发送方确实发送了信息;防止伪造:其他人不能伪造对信息的签名,因为私钥只有签名者自己知道.

3 结 论

政府在网上办公已经成为一种趋势,但是在公文的传输和签名中,安全性和效率是制约其发展的重要因素之一,因此一个安全的公文传输解决方案是非常必要的.本文首先对组成椭圆曲线密码系统的点乘算法的效率进行提高,然后利用椭圆曲线密码体制来实现公文的数字签名,同时采用共享密钥对发送的公文进行加密,满足了电子政务系统的安全性要求,解决了认证性、机密性、完整性、不可否认性,使得安全性、有效性均得到了提高.

[1]Qiu Qizhi,Xiong Qianxing.Research on Elliptic Curve Cryptograph[J].The 8th International Conference on Computer Supported Cooperative Work in Design Proceedings,2004:698-701.

[2]Rahim Ali.Elliptic Curve Cryptography A New Way for Encryption[J].International Symposium on Biometric and Security Technologies,2008:1-5.

[3]刘双根,李 萍,胡予濮.椭圆曲线密码中标量算法的改进方案[J].计算机工程,2006,32(17):28-29.

[4]Wang Bangju,Zhang Huanguo,Wang Yuhua.An Efficient Elliptic Curves Scalar Multiplication for Wireless Network[J].2007 IFIP Intermational Conference on Network and Parallel Computing Workshops,2007:131-134.

[5]Daisuke Adachi,Tomio Hirata.Combination of Mixed Coordinates Strategy and Direct Computations for Efficient Scalar M ultiplications[J].2005 IEEE Pacific Rim Conference on Communications,Computers and Signal Processing,2005:117-120.